| Главная » Статьи » Физика » Асимптота |
Общий метод отыскания асимптоты
 Общий метод отыскания асимптоты Укажем теперь общий метод отыскания асимптоты, то есть способ определения коэффициентов k и l в уравнении y = kx + l. Будем рассматривать для определённости лишь случай х ® + ¥ (при х ® - ¥ рассуждения проводятся аналогично). Пусть график функции f имеет асимптоту y = kx + l при х ® + ¥. Тогда, по определению, f (x) = kx + l + 0 Разделим обе части равенства f (x) = kx + l + 0 на х и перейдём к пределу при х ® + ¥. Тогда lim 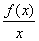 = k. = k. х ® + ¥ Используя найденное значение k, получим из f (x) = kx + l + 0 для определения l формулу l = lim (f (x) – kx). х ® + ¥ Справедливо и обратное утверждение: если существуют такие числа k и l, что выполняется условие l = lim (f (x) – kx), то прямая y = kx + l является х ® + ¥ асимптотой графика функции f (x). В самом деле, из l = lim (f (x) – kx) имеем х ® + ¥ lim [f (x) - (kx + l)] = 0, х ® + ¥ то есть прямая y = kx + l действительно удовлетворяет определению асимптоты, иначе говоря, выполняется условие f (x) = kx + l + 0. Таким образом, формулы lim 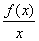 = k. и l = lim = k. и l = lim(f (x) – kx) х ® + ¥ х ® + ¥ сводят задачу отыскания асимптот y = kx + l к вычислению пределов определённого вида. Более того, мы показали, что если существует представление функции f в виде f (x) = kx + l + 0, то k и l выражаются по формулам lim 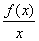 = k. = k.и l = lim (f (x) – kx) х ® + ¥ х ® + ¥ Следовательно, если существует представление y = kx + l, то оно единственно. Найдём по этому правилу асимптоту графика функции f (x) = 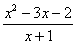 , ,найденную нами выше другим способом: 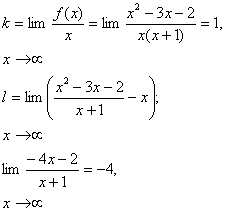 7 7 то есть мы, как и следовало ожидать, получили тоже уравнение асимптоты y = x – 4, как при х ® + ¥, так и при х ® - ¥. В виде y = kx + l может быть записано уравнение любой прямой, непараллельной оси Oy. Естественно распространить определение асимптоты и на прямые, параллельные оси Oy. | |
| Просмотров: 748 | |
| Всего комментариев: 0 | |
Категории раздела
| Фракталы [10] |
| Асимптота [6] |
| Физика [11] |
| Опыты [4] |
| Метод Зойтендейка [3] |
| Nikola Tesla [12] |
| Метафизика [10] |
| Мари Кюри [3] |
| Задача равновесия [14] |
Друзья сайта