| Главная » Статьи » Физика » Физика |
Вывод и анализ формул Френеля на основе электромагнитной теории Максвелла.
Постановка задачи Пусть имеются две
диэлектрические среды 1 и 2 , с электрической и магнитной проницаемостью ξ1,μ1 и
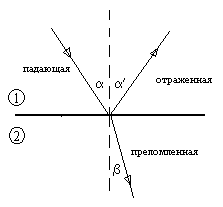
рис.1 Данная волна должна представлять
собой точное решение уравнений Максвелла : для плоской монохроматической волны точное решение этих уравнений будет (если оси Х направить в сторону распространения волны):
где A и B , φ и ⍦, ⍵- постоянные (не зависят от времени и координаты) , и ξ и μ- характеристики среды , в которой распространяется волна , τ =t-x/V , t - рассматриваемый момент времени x - рассматриваемая координата на оси Х V - скорость распространения волны в данной среде (естественно , в силу линейности уравнений Максвелла любая сумма таких волн будет также их точным решением ) Также она должна удовлетворять условиям на границе раздела : Eτ и Bn не терпят разрыва на поверхности раздела , Hτ и Dn также не терпят разрыва , поскольку на границе раздела не течет ток и нет поверхностной плотности заряда: (индексом 1 обозначаем все , относящееся к первой среде , индексом 2 - ко второй) Таким образом , необходимо построить точное решение уравнений (1) , удовлетворяющих условиям (3). Для этого рассмотрим два случая : случай ТМ -волны (р-волны ) - вектор Ĥ перпендикулярен плоскости падения (трансверсальная магнитная) , и случай ТЕ-волны (s-волны)- вектор Ē перпендикулярен плоскости падения (трансверсальная электрическая). Любая плоская волна (с любой поляризацией) может быть представлена как линейная комбинация двух таких волн. Случай ТМ -волны (p - волны)
рис.2 Из рисунка видео , что
подставляем значения Eτ :
подставляем Ey из (2) :
Аналогично , поскольку
для выполнения равенств для Eτи Hτ потребуем равенства аргументов косинусов :
потребуем также равенства начальных фаз: φ1=φ1’=φ2=φ из рисунка видно , что : θ1= α,θ’1= π - α’,θ2= β , (4) (α,α’и β - соответственно : угол падения , угол отражения и угол преломления ) , тогда имеем :
из равенства аргументов получаем :
(т.к.
разделим теперь выражения для Eτ и Hτ на
здесь неизвестными являются A2 и A’1, , а A1 - заданно. Умножим первое уравнение на
поскольку для неферромагнетиков магнитная проницаемостьμ незначительно отличается от единицы , то для сравнительно широкого класса сред можно считать μ1= μ2, тогда:
( разделим числитель и
знаменатель на применив закон преломления , получим (6):
из второго уравнения системы (5) получаем для A2:
проверим теперь выполнение еще
двух условий на границе раздела ,которые мы не учли - из рисунка видно , что
Таким образом действительно получено точное решение уравнений (2) , удовлетворяющее всем начальным условия. Итак , имеем следующие формулы Френеля для случая s-волны для отражения и преломления (из (6) и (7) ):
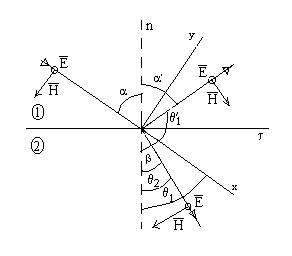
Случай ТЕ -волны ( s - волны)
рис.3 Из рисунка видно , что Условия (3) для Hτ и Eτ: и
подставляя значения E и H из (2) получим :
умножим первое уравнение на
поскольку мы полагаем
из второго уравнения системы (8) получаем:
проверим теперь неучтенные
условия на границе раздела : Второе условие выполняется ,
поскольку
подставляем B2 из второго уравнения системы (8) :
таким образом мы действительно нашли точное решение уравнений (2) , удовлетворяющее всем начальным условиям . В случае p-волны имеем следующие формулы Френеля для отражения и преломления (из (9) и (10))
Анализ формул Френеля Исследуем отношения энергий
(точнее плотности потока энергий ) падающей и отраженной ТМ и ТЕ волн и
падающей и прошедшей волн в зависимости от угла падения α. Для этого рассмотрим
отношение нормальной составляющей вектора Пойтинга и ƒz) волн. Тогда с из полученных формул Френеля для отражения и преломления , с учетом (2) будем иметь:
А. Отражение Исследуем
сначала поведение при α →0(просто положить α равным нулю нельзя , потому что будет неопределенность ):
для случая падения из воздуха в
стекло (n=153) : т.е. это величина порядка нескольких процентов (можно заметить , что если поменять среды местами - т.е. рассматривать падение из воды в воздух , то это значение не изменится) В случае
падения из оптически менее плотной среды в оптически более плотную при
Действительно, преломленной волны при скользящем падении не образуется и интенсивность падающей волны не меняется. В случае падения из оптически более плотной среды в оптически менее плотную , необходимо учесть явление полного внутреннего отражения , когда прошедшей волны нет - вся волна отражается от поверхности раздела. Это происходит при значениях α больших , чем αxp, вычисляемого следующим образом:
Для падения из стекла в воздух Здесь не рассматривается полное внутреннее отражение , поэтому α в случае падения из оптически более плотной среды в оптически менее плотную изменяется до αxp, в этом случае:
Далее исследуем поведение этих
функций между крайними точками , для этого исследуем на монотонность функции: Нам понадобится производная
Знак этой производной ,(
поскольку есть >0 при
Знак функции при
Это есть угол Брюстера ( При Итак , в обоих случаях rp сначала монотонно убывает
от
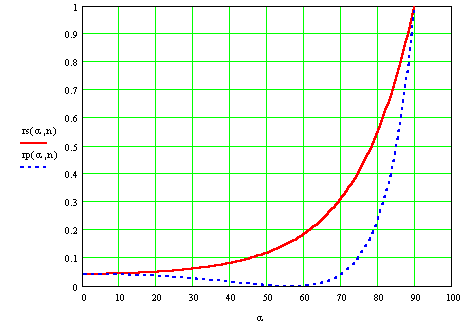
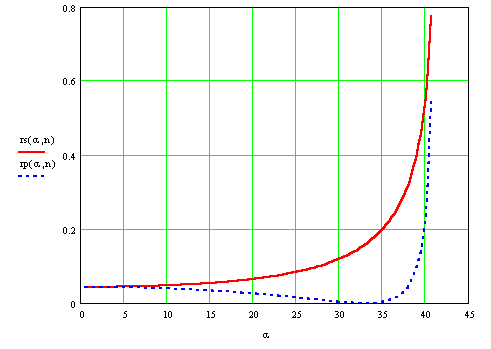
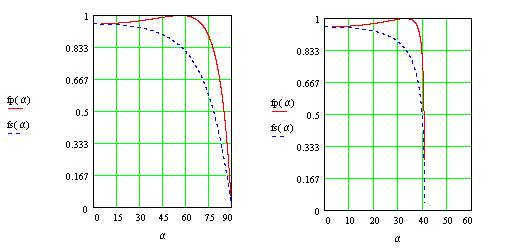
Полученные зависимости иллюстрируются следующими графиками : на первом показана зависимость
на втором -для случая падения волны из стекла в воздух
В. Преломление Для
анализа поведения Действительно , проверим это :
рассмотрим отдельно числитель:
Таким образом , используя
предыдущее исследование
Для случая падения из воздуха в
стекло (а можно заметить , что если среды поменять местами , то это значение не
изменится )
Между этими точками Окончательно ,
С. Набег фаз при отражении и преломлении Из формул Френеля следует , что
отношения , В случае отраженной p-волны при n>1 больше
0 при В случае отраженной s-волны В случае произвольно падающей линейно поляризованной волны , которая представляется в виде суммы p и s-волн , в отраженной волне , таким образом , можно получить , в общем случае волну произвольной (эллиптической) поляризации . Для исследования сдвига фаз в прошедшей волне , воспользуемся соотношениями , возникшими как промежуточные результаты при выводе (7) и (10) : из этих соотношений видно , что ,
поскольку | |
| Просмотров: 3500 | |
| Всего комментариев: 0 | |
| Фракталы [10] |
| Асимптота [6] |
| Физика [11] |
| Опыты [4] |
| Метод Зойтендейка [3] |
| Nikola Tesla [12] |
| Метафизика [10] |
| Мари Кюри [3] |
| Задача равновесия [14] |
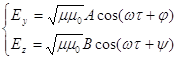 и
и 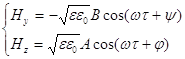 (Ex = Hx = 0) (2)
(Ex = Hx = 0) (2)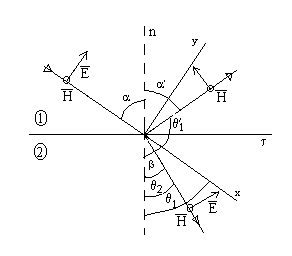
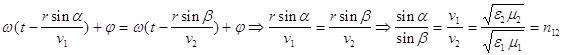 т.е.
получены , как и следовало ожидать , законы отражения и преломления света
т.е.
получены , как и следовало ожидать , законы отражения и преломления света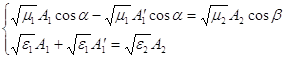 (5)
(5)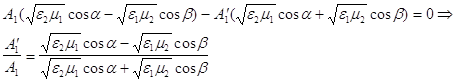
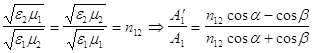 .
.
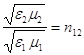 )
) 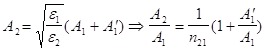 (поскольку полагаем μ1=μ2,) , тогда:
(поскольку полагаем μ1=μ2,) , тогда: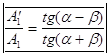 и
и 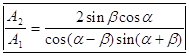
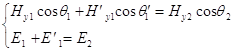
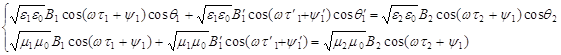 как
и в случае ТМ-волны предполагаем равенство аргументов косинусов и совершенно
аналогично получаем в этом случае закон отражения и преломления света ,
сокращая на
как
и в случае ТМ-волны предполагаем равенство аргументов косинусов и совершенно
аналогично получаем в этом случае закон отражения и преломления света ,
сокращая на 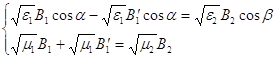 (8)
(8)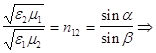
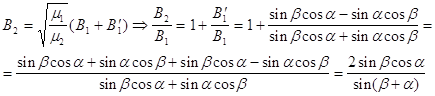 (10)
(10)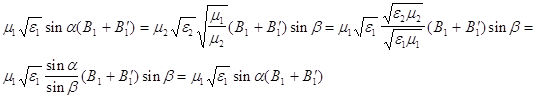
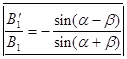 и
и 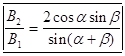
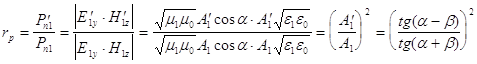
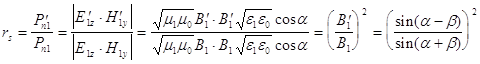
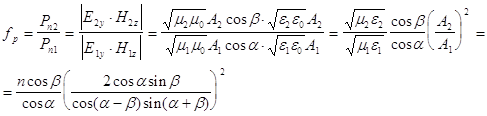
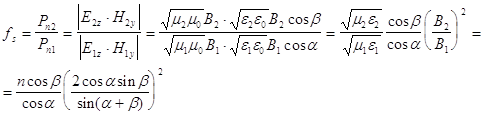
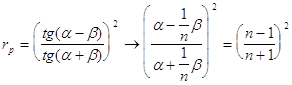
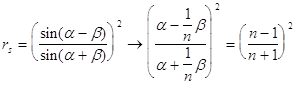
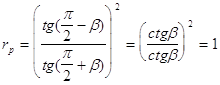
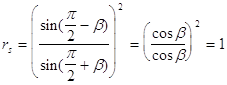
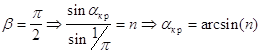
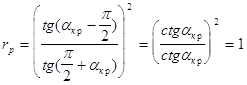
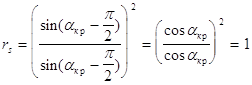
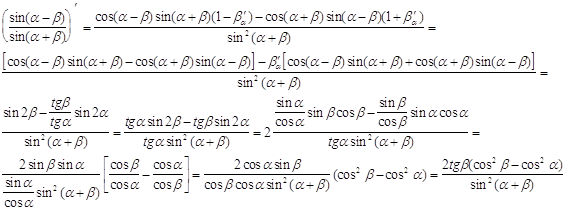 Знак этой производной ( поскольку
Знак этой производной ( поскольку
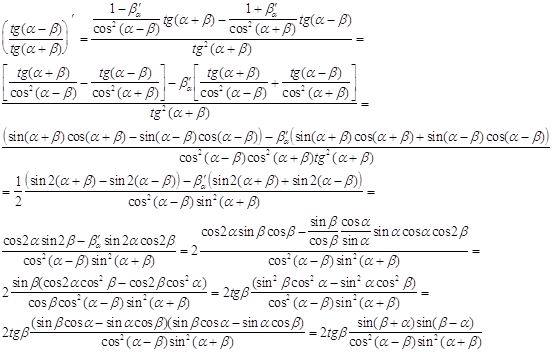
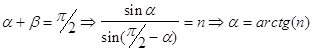
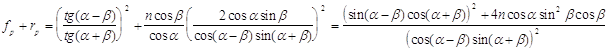
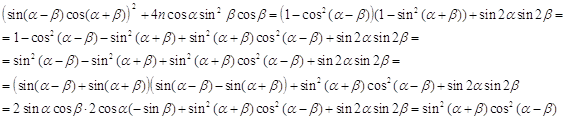 таким образом действительно
таким образом действительно 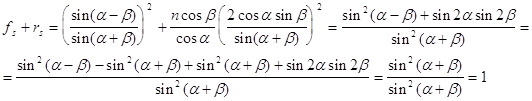
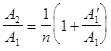 и
и 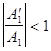 и
и 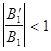 , то всегда
, то всегда