| Главная » Статьи » Физика » Фракталы |
Аттрактор Лоренца
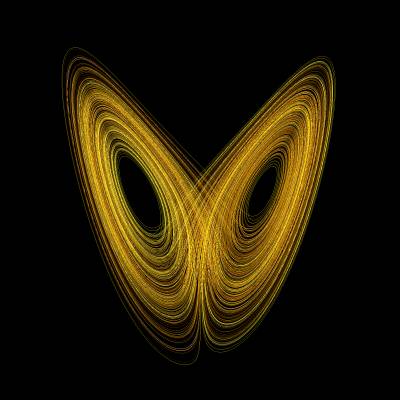 Аттрактор Лоренца До настоящего момента мы изучали фракталы, которые являются статическими фигурами. Наш подход вполне приемлем до тех пор, пока не возникает необходимость рассмотрения таких природных явлений, как падающие потоки воды, турбулентные завихрения дыма, метеосистемы и потоки на выходе реактивных двигателей. В этих случаях один-единственный фрактал соответствует моментальному снимку данного феномена. Структуры, изменяющиеся во времени, мы определяем как динамические системы. Интуитивно понятно, что динамической противоположностью фрактала является хаос. Это означает, что хаос описывает состояние крайней непредсказуемости, возникающей в динамической системе, в то время как фрактальность описывает крайнюю иррегулярность или изрезанность, присущую геометрической конфигурации. Достаточно скоро стало ясно, что многие хаотические динамические системы, описывающие феномены окружающего нас мира, устроены очень сложно и не могут быть представлены традиционными методами математического анализа. По- видимому, нет никакой возможности получить математические выражения для решений в замкнутом виде, даже если использовать бесконечные ряды или специальные функции. Рассмотрим знаменитый пример, весьма наглядно демонстрирующий, что стоит за термином «хаотическая динамика». Эдвард Лоренц из Массачусетского технологического института в 1961 году занимался численными исследованиями метеосистем, в частности моделированием конвекционных токов в атмосфере [1]. Он написал программу для решения следующей системы дифференциальных уравнений: dx/dt = s(-x + y), dy/dt = rx – y – xz, dz/dt = -bz + xy. В дальнейших расчетах параметры s, r и b постоянны и принимают значения s = -10, r = 28 и b = 8/3. Согласно описанию эксперимента, принадлежащему самому Лоренцу, он вычислял значения решения в течение длительного времени, а затем остановил счет. Его заинтересовала некоторая особенность решения, которая возникала где-то в середине интервала счета, и поэтому он повторил вычисления с этого момента. Результаты повторного счета, очевидно, совпали бы с результатами первоначального счета, если бы начальные значения для повторного счета в точности были равны полученным ранее значениям для этого момента времени. Лоренц слегка изменил эти значения, уменьшив число верных десятичных знаков. Ошибки, введенные таким образом, были крайне невелики. Но самое неожиданное было впереди. Вновь сосчитанное решение некоторое время хорошо согласовывалось со старым. Однако, по мере счета расхождение возрастало, и постепенно стало ясно, что новое решение вовсе не напоминает старое (рисунки приведены в [1], стр. 149). Лоренц вновь повторял и проверял вычисления (вероятно, не доверяя компьютеру), прежде чем осознал важность эксперимента. То, что он наблюдал, теперь называется существенной зависимостью от начальных условий --- основной чертой, присущей хаотической динамике. Существенную зависимость иногда называют эффектом бабочки. Такое название относится к невозможности делать долгосрочные прогнозы погоды. Сам Лоренц разъяснил это понятие в статье «Предсказуемость: может ли взмах крылышек бабочки в Бразилии привести к образованию торнадо в Техасе?», опубликованной в 1979 году [3, стр. 322]. Несмотря на большую значимость эксперимента Лоренца, в данной курсовой работе не будут рассматриваться модели, связанные с динамическими системами, описываемыми дифференциальными уравнениями. Напротив, мы будем рассматривать наиболее простые модели хаотической динамики --- дискретные, к которым относится знаменитое и вездесущее множество Мандельброта и сопутствующие ему множества Жюлиа. Рис. 4.1.1. Аттрактор Лоренца. 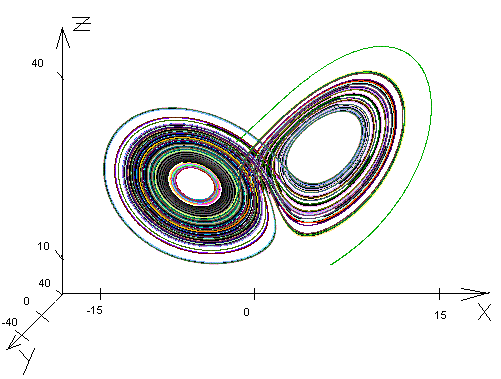 | |
| Просмотров: 1663 | |
| Всего комментариев: 0 | |
Категории раздела
| Фракталы [10] |
| Асимптота [6] |
| Физика [11] |
| Опыты [4] |
| Метод Зойтендейка [3] |
| Nikola Tesla [12] |
| Метафизика [10] |
| Мари Кюри [3] |
| Задача равновесия [14] |
Друзья сайта