| Главная » Статьи » Математика » Теория вероятности |
Распределения Бернулли и Пуассона.Пусть проводятся n испытаний по схеме Бернулли (см. 4.4.3.). Событие А может произойти в результате этой серии опытов 0 раз, 1 раз, … n раз. Рассмотрим случайную величину — число испытаний в которых событие А произошло. Имеем дискретную с.в. с законом распределения
Также говорят, что с.в. Х распределена по биномиальному закону с параметрами n и P и пишут X → B(n,p). Если n=1, то говорят, что с.в. Х имеет распределение Бернулли параметром P. Теорема. Пусть X1,X2,...Xn — независимые с.в. распределенные по Бернулли с одинаковым параметром P. Пусть . Sn=X1+X2+...+Xn Тогда Sn → B(n,p). Числовые характеристики биномиального закона. M(X) = n · p, .D(X) = n·p·q Если n — велико, а P — мало, то вычисления
вероятности по формуле Нормальное распределениеОпределение и значениеБольшинство экспериментальных исследований, в том числе и в области правоведения, связано с измерениями, результаты которых могут принимать практически любые значения в заданном интервале и, как уже было отмечено, описываются моделью непрерывных случайных величин. Поэтому в дальнейшем будут рассматриваться в основном непрерывные случайные величины и связанные с ними непрерывные распределения. Одним из непрерывных распределений, имеющим основополагающую роль в математической статистике, является нормальное, или гауссово, распределение. Нормальное распределение является самым важным в статистике. Это объясняется целым рядом причин. 1. Прежде всего, многие экспериментальные наблюдения можно успешно описать с помощью нормального распределения. Следует сразу же отметить, что не существует распределений эмпирических данных, которые были бы в точности нормальными, поскольку (как будет показано ниже) нормально распределенная случайная величина находится в пределах от ∞ до +∞, чего никогда не бывает на практике. Однако нормальное распределение очень часто хорошо подходит как приближение. Проводятся ли измерения IQ, роста и других физиологических параметров — везде на результаты оказывает влияние очень большое число случайных факторов (естественные причины и ошибки измерения). Причем, как правило, действие каждого из этих, факторов незначительно. Опыт показывает, что результаты именно в таких случаях будут распределены приближенно нормально. 2. Нормальное распределение хорошо подходит в качестве аппроксимации (приближенного описания) других распределений (например, биномиального). 3. Многие распределения, связанные со случайной выборкой, при увеличении объема последней переходят в нормальное. 4. Нормальное распределение обладает рядом благоприятных математических свойств, во многом обеспечивших его широкое применение в статистике. В то же время следует отметить, что в природе встречается много экспериментальных распределений, для описания которых модель нормального распределения малопригодна. Для этого в математической статистке разработан ряд методов, некоторые из которых приводятся в следующих главах. Говорят, что с.в. распределена по нормальному закону с параметрами m и σ и записывать X→N(m,σ²) если ее плотность вероятностей задается следующим образом
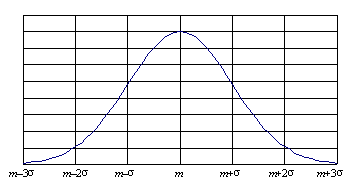
(4.23) График плотности (нормальная кривая) представлен на рис. 4.10. Укажем основные свойства нормального распределения N(m,σ²) . 1. Нормальная кривая имеет колоколообразную форму, симметричную относительно точки x= m , с точками перегиба, абсциссы которых отстоят от m на ±σ., 2. Для нормального распределения математическое ожидание M(X) = m, дисперсия равна σ² и, следовательно, стандартное отклонение равно σ. 3. Как видно из выражения (4.23), нормальное распределение полностью определяется двумя параметрами: m и σ — математическим ожиданием и стандартным отклонением. График плотности вероятности нормального распределения показывает, что для нормально распределенной случайной величины вероятность отклонения от среднего значения m быстро уменьшается с ростом величины отклонения. 4. Медиана и мода нормального распределения совпадают и равны математическому ожиданию m. 5. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю (γ3 = 0,γ4 = 0) Последнее свойство (5) используется для проверки предположения о нормальности распределения генеральной совокупности (гл. 6).
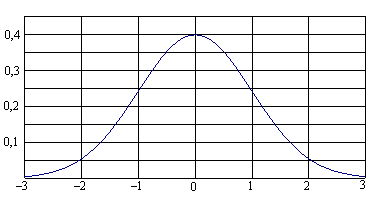
Рис. 4.10. Плотность вероятностей нормального распределения Нормированное нормальное распределениеФормула (4.23) описывает целое семейство нормальных кривых, зависящих, как было сказано выше, от двух параметров —m и σ, которые могут принимать любые значения, поэтому возможно бесконечно много нормально распределенных совокупностей. Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая по достаточно сложной формуле (4.23), используют так называемое нормированное (или стандартное) нормальное распределение N(0;1), для которого составлены подробные таблицы. Нормированное нормальное распределение имеет параметры m = 0 и σ = 1 . Это распределение получается, если пронормировать нормально распределенную величину X по формуле: Плотность распределения вероятностей нормированного нормального распределения записывается в виде: На кривой нормированного нормального распределения (рис. 4.11) указаны в процентах доли площадей соответствующих отмеченным значениям нормированного отклонения и, по отношению к общей площади под кривой, равной 1 (100%). Эти площади определяют вероятности попадания случайной величины в соответствующие интервалы.
Рис. 4.11. Нормированное нормальное распределение Таблица значений — ординат нормальной кривой приведена в специальных таблицах. Значения φ(u) для некоторых характерных нормированных отклонений представлены в табл. 4.1. Таблица 4.1 Ординаты нормальной кривой
Вероятность попадания в заданный интервалОчень часто исследователя интересует вопрос: какова вероятность того, что изучаемый признак генеральной совокупности находится в заданных границах (например, вероятность того, что результат измерения IQ для группы испытуемых окажется в пределах 115 — 125)? Если предполагается нормальное распределение признака в генеральной совокупности, то получить ответ на этот вопрос очень просто. Как говорилось ранее, вероятность попадания нормально распределенной
случайной величины в заданный интервал [x1,x2] можно определить
по функции распределения: Итак, вероятность попадания с.в. U-->N(0;1) в заданный интервал:
, где Ф — принятое обозначение для функции нормированного нормального распределения которое имеет следующий вид: при этом Ф-(u) = 1-Ф(u) . Часто представляет интерес вероятность попадания с.в. U → N(0;1) в симметричный интервал. Тогда
Учитывая свойства функции Лапласа, получаем: Интеграл, входящий в выражение (4.25), не выражается в элементарных функциях, поэтому для вычисления функции Ф(u) используют вспомогательную функцию — функцию Лапласа (интеграл вероятностей):
(4.26) который табулируется. Функция Лапласа является нечетной, т.е. Ф0(-u)=–Ф0(u). В книгах по теории вероятности приведена либо таблица значений функции Лапласа Ф0(u) , Ф(u)либо . Чтобы найти вероятность попадания нормально распределенной случайной величины X→N(m,σ²) в заданный интервал [X1;X2] с помощью функции Лапласа, сначала с.в. X ормализуется (см. 4.24), а затем используется следующая формула:
= Пример Вычислить P(0,74<X<3,26)< если X→N(2,9) . Решение. | |||||||||||||||||||||||||||||||||||||
|
Границы интервала, m± x |
m±0,5σ | m ± σ |
m±2σ |
m±3σ |
|
Вероятность попадания в интервал |
0,3829 |
0,6827 |
0,9545 |
0,9973 |
Из табл. 4.2 следует, что P[-3σ<(X - m)<3σ = 0,9973.
Это выражение известно в статистике как "правило трех сигм”. Оно означает, что с вероятностью 0,9973 (практически с единичной) нормально распределенная случайная величина окажется в пределах ±3σ от среднего значения. Иначе говоря, отклонения от среднего больше чем на +3σ можно ожидать примерно в 1 случае из 370 испытаний.
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
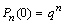
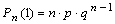
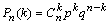
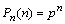
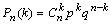 на практике
невозможно. При этих условиях используется формула Пуассона для
вычисления вероятности маловозможных событий в массовых испытаниях:
на практике
невозможно. При этих условиях используется формула Пуассона для
вычисления вероятности маловозможных событий в массовых испытаниях: 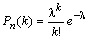 , где λ=np , k!=1·2·...·k , 0! = 1.
Соответствующая с.в. распределена по закону Пуассона.
, где λ=np , k!=1·2·...·k , 0! = 1.
Соответствующая с.в. распределена по закону Пуассона.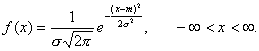
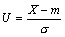 (4.24)
(4.24)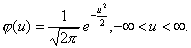
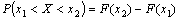 или с помощью
функции плотности вероятностей:
или с помощью
функции плотности вероятностей: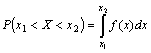 .
.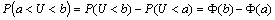
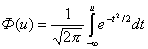 , (4.25)
, (4.25)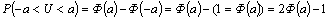
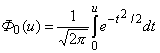
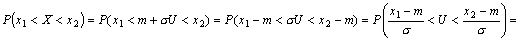
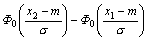 (4.27)
(4.27)