| Главная » Статьи » Математика » Теория вероятности |
Решения задач по теории вероятностей
Условное математическое ожидание 000252Найти условное математическое ожидание составляющей Y при
Решение 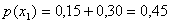 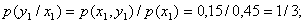 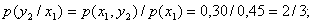 Условное математическое ожидание: 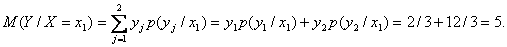 Плотность вероятности 000251Нормально распределенная случайная величина Х задана своими параметрами –а =2 – математическое ожидание и σ = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2. Решение Плотность распределения имеет вид: 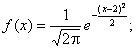 Построим график: 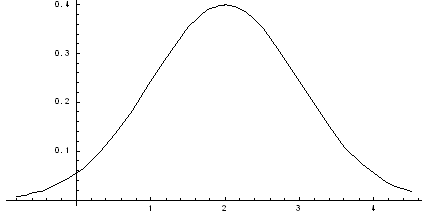 Найдем вероятность попадания случайной величины в интервал (1; 3).  Найдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2. 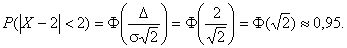 Тот же результат может быть получен с использованием нормированной функции Лапласа. 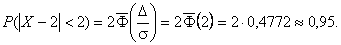 Нормальное распределение случайной величины 000250Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина,распределенная по нормальному закону с математическим ожидание а = 65 т и средним квадратичным отклонением σ = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. Решение Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100*65 = 6500) не превосходит 6600 – 6500 = 100 т. Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально. Получаем:  Закон распределения величины 000249В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар,причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию. Решение Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте). Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна 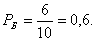 Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий. 1) Белый шар не появился вовсе: 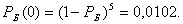 2) Белый шар появился один раз: 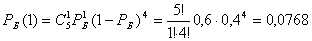 3) Белый шар появиться два раза: 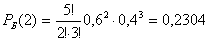 4) Белый шар появиться три раза: 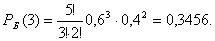 5) Белый шар появиться четыре раза: 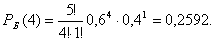 6) Белый шар появился пять раз: 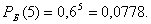 Получаем следующий закон распределения случайной величины Х.
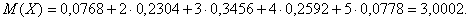 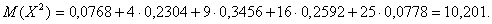 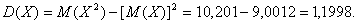 Найти функцию распределения 000248Задана непрерывная случайная величина х своей функцией распределения f(x).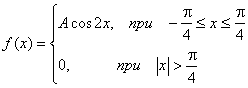 Требуется определить коэффициент А, найти функцию распределения, построить график плотности распределения. Решение Найдем коэффициент А. 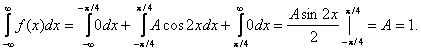 Найдем функцию распределения: 1) На участке 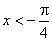 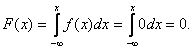 : 2) На участке  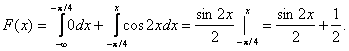 3) На участке 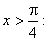 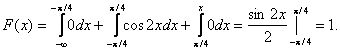 Итого: 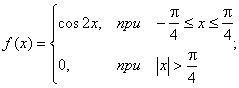 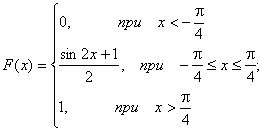 Построим график плотности распределения: 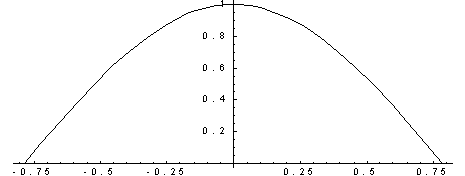 f(x) График плотности распределения 000247Случайная величина подчинена закону распределения с плотностью: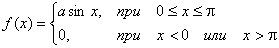 Требуется найти коэффициент а и построить график плотности распределения. Решение Построим график плотности распределения: 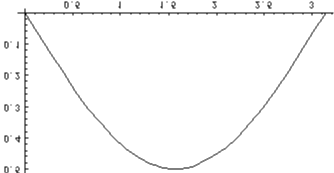 Для нахождения коэффициента а воспользуемся свойством 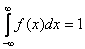 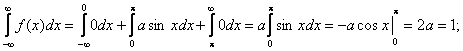 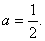 Вероятность события 000245Производятсянезависимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63. Решение По формуле дисперсии биноминального закона получаем:  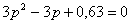 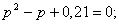 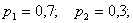 Дисперсия дискретной случайной величины 000244Найти дисперсию дискретной случайной величины Х – числа появленийсобытия А в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что М(Х) = 0,9. Решение Т.к. случайная величина Х распределена по биноминальному закону, то 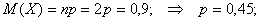 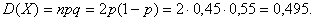 Математическое ожидание, дисперсия 000243Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта.Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины Х. Решение Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96. Таким образом, закон распределения может считаться биноминальным. 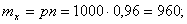 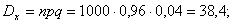 Случайная величина: математическое ожидание, дисперсия 00024Закон распределения случайной величины имеет вид:
Найти математическое ожидание и дисперсию случайной величины. Решение Математическое ожидание случайной величины равно: 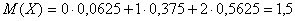 Возможные значения квадрата отклонения: 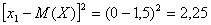 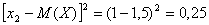 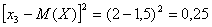 Тогда
Дисперсия равна: 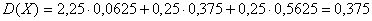 Биноминальный закон 000241Двеигральные кости одновременно бросают 2 раза. Написать биноминальный закон распределения дискретной случайной величины Х – числа выпадений четного числа очков на двух игральных костях. Решение Каждая игральная кость имеет три варианта четных очков – 2, 4 и 6 из шести возможных, таким образом, вероятность выпадения четного числа очков на одной кости равна 0,5. Вероятность одновременного выпадения четных очков на двух костях равна 0,25. Вероятность того, что при двух испытаниях оба раза выпали четные очки на обеих костях, равна: 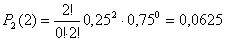 Вероятность того, что при двух испытаниях один раз выпали четные очки на обеих костях: 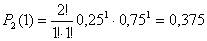 Вероятность того, что при двух испытаниях ни одного раза не выпаде четного числа очков на обеих костях: 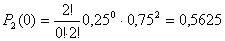 Биноминальный закон распределения 000240В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написатьбиноминальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения. Решение Вероятность появления нестандартной детали в каждом случае равна 0,1. Найдем вероятности того, что среди отобранных деталей: 1) Вообще нет нестандартных. 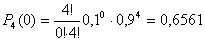 2) Одна нестандартная. 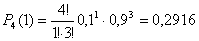 3) Две нестандартные детали. 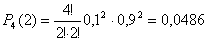 4) Три нестандартные детали. 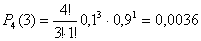 5) Четыре нестандартных детали. 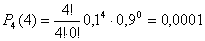 Многоугольник распределения 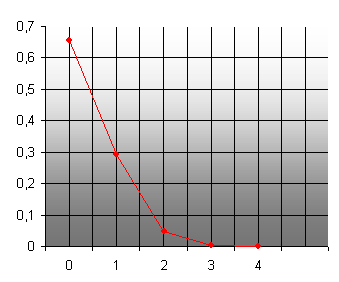 Вероятность шара 000239В урне 3 белых и 5 черных шаров. Из урны вынимают наугад два шара. Найти вероятность того, что эти шары не одного цвета.Решение Событие, состоящее в том, что выбранные шары разного цвета произойдет в одном из двух случаев: 1) Первый шар белый (вероятность – 3/8), а второй – черный (вероятность – 5/7). 2) Первый шар черный (вероятность – 5/8), а второй – белый (вероятность – 3/7). Окончательно получаем: 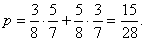 Несовместные события 000238Имеютсядве партии однородных деталей. Первая партия состоит из 12 деталей, 3 из которых - бракованные. Вторая партия состоит из 15 деталей, 4 из которых – бракованные. Из первой партии извлекаются наугад 5 деталей, а из второй – 7 деталей. Эти детали образуют новую партию. Какова вероятность достать из них бракованную деталь? Решение Для того, чтобы выбранная наугад деталь была бы бракованной, необходимо выполнение одного из двух несовместных условий: 1) Выбранная деталь была из первой партии (вероятность – 5/12) и при этом она – бракованная (вероятность – 3/12). Окончательно: 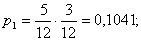 2) Выбранная деталь была из второй партии (вероятность – 7/12) и при этом она – бракованная (вероятность – 4/15). Окончательно: 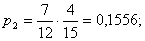 Окончательно, получаем: 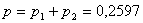 Вероятность детали 000237Имеются две партии однородных деталей. Первая партия состоит из 12деталей, 3 из которых - бракованные. Вторая партия состоит из 15 деталей, 4 из которых – бракованные. Из первой и второй партий извлекают по две детали. Какова вероятность того, что среди них нет бракованных деталей. Решение Вероятность оказаться не бракованной для первой детали, извлеченной из первой партии, равна р1=9/12, для второй детали, извлеченной из первой партии при условии, что первая деталь была не бракованной р2=8/11. Вероятность оказаться не бракованной для первой детали, извлеченной из второй партии, равна р3=11/15, для второй детали, извлеченной из второй партии при условии, что первая деталь была не бракованной р4=10/14. Вероятность того, что среди четырех извлеченных деталей нет бракованных, равна: 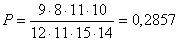 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 26005 | Комментарии: 1 | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 1 | |||||||||||||||||||||||||||||
Категории раздела
Друзья сайта
| |||||||||||||||||||||||||||||