| Главная » Статьи » Математика » Теория вероятности |
Схема Бернулли. Примеры решения задач
| Схема Бернулли. Примеры решения задач Не будем долго размышлять о высоком — начнем сразу с определения. Определение Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз. Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы. Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода: 1. A — появление события A с вероятностью p; 2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p. Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p. Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности. Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы: Теорема Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле: 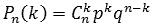 где Cnk — число сочетаний, q = 1 − p. Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным. Задача Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10. Решение По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия. Таким образом, имеем: n = 10; p = 0,8; q = 0,2. Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10): 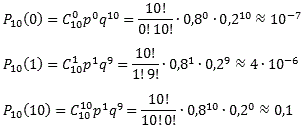 Ответ 10−7; 4 • 10−6; 0,1 Задача Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что: 1. герб выпадет три раза; 2. герб выпадет один раз; 3. герб выпадет не менее двух раз. Решение Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз. Таким образом, имеем: n = 6; p = 0,5; q = 0,5. Определим вероятность того, что герб выпал три раза, т.е. k = 3: 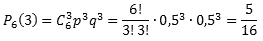 Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1: 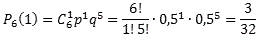 Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P6(2) + P6(3) + ... + P6(6). Заметим, что эта сумма также равна (1 − P6(0) − P6(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P6(1) нам уже известно, осталось найти P6(0): 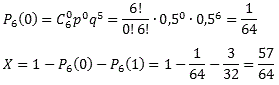 Ответ 1) 5/16; 2) 3/32; 3) 57/64 Задача Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три? Решение Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8. Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8. Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3): 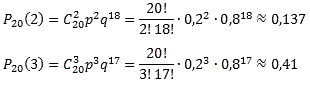 Очевидно, P20(3) > P20(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая. Ответ P20(3) > P20(2) Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению. P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь. | |
| Просмотров: 22990 | Комментарии: 2 | |
| Всего комментариев: 2 | ||||||||||||||||||||||||||||||
Категории раздела
Друзья сайта
| ||||||||||||||||||||||||||||||