| Главная » Статьи » Математика » Геометрия |
Построения на изображениях плоских фигур
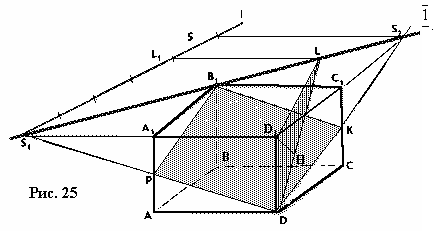
| . Построения на изображениях плоских фигур. До выполнения построений решим опорные задачи. Задача 2. Найти отношение АН:АС (или СН:СА), где точка Н- основание высоты ВН треугольника АВС. Решение. При способе выносных чертежей необходимо построить треугольник A0 B0C0 – выносной чертеж треугольника АВС. В треугольнике A 0B0C0 построим высоту B0Н0 , имеем и отрезок A0Н0 , значит, отношение A0Н 0:А0C0 станет известным. Так как АН║АС и при параллельном проектировании отношение длин параллельных отрезков сохраняется, то искомое отношение АН:АС равно отношению A0Н0:А0 C0 . 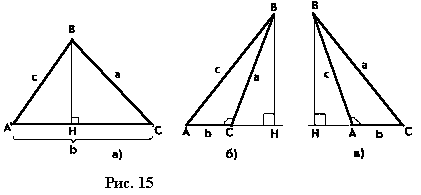 Чтобы найти отношение АН:АС вычислительным способом, следует подсчитать сначала стороны треугольника АВС, затем, выразив ВН2 из прямоугольных треугольников АВН и СВН, получить равенство АВ2-АН2=ВС 2-СН2. Полагая в этом равенстве для краткости АВ = с, ВС= а и АС=b? , будем иметь: с2-АН2=а 2-СН2 (1). Это равенство является основой для вычисления одного из отрезков АН или СН. Независимо от вида треугольника АВС (рис. 15 а, б, в), сделав в равенстве (1) замену меньшего из двух отрезков СН или АН, т. е. полагая СН2=(b -АН)2 в случае, когда СН≤АН, или АН2=(b-СН) 2 в случае, когда АН<СН. Из уравнения с2-АН2 =а2-(b-АН)2 найдем АН и затем искомое отношение АН:АС, или из уравнения с2-(b-СН)2 =а2-СН2 найдем СН и затем отношение СН:СА. Задача 3. Построить точку Х, делящую данный отрезок АС в отношении АХ:АС=p:q , в следующих случаях: а) p и q – известные отрезки; б) p и q – известные целые положительные числа. А. Решение. На вспомогательном луче l, проведенном через точку А (рис. 16, а, б), построим отрезки АХ1=kp и АС1=kq , где k>0. Например, на рисунках 16, а, б взято k=2. Точку С1 соединим с точкой С и через точку Х1 проведем прямую, параллельную прямой СС1. Точка пересечения построенной прямой со вспомогательным лучомlи будет искомой точкой Х. На рисунке 16, а построение выполнено при условии p<q, а на рисунке 16, б – при условии p>q. Б. Решение. Выберем некоторый отрезок е в качестве единичного отрезка. На вспомогательном луче l, проведенном через точку А, построим отрезки АХ1=pe и АС1= qe. Дальнейшие построения сделаны, как в пункте а). Они понятны из рисунка 16, в. 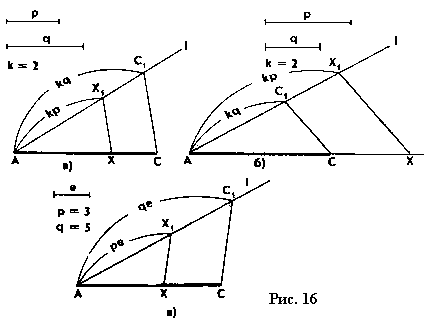 Основными способами решения задач построения на изображениях плоских фигур являются: Основными способами решения задач построения на изображениях плоских фигур являются: 1. Способ выносных чертежей. 2. Вычислительный способ. 3. Геометрический способ. Задача 4. Параллелограмм АВСD является изображением квадрата A0B 0C0D0 , на стороне A0B0 которого взята точка Е0 – середина этой стороны, на стороне A0 D0 взята точка F0, такая, что A0F0:A 0D0=1:4, и на прямой A0D0 взята точка К 0, такая, что точка D0 – это середина отрезка A0К 0 . Через точку К0 проведена прямая x0, перпендикулярная прямой Е0F0. Построить изображение прямой x0. Решение. Способ выносных чертежей (рис. 17, а). Так как при параллельном проектировании отношение длин параллельных отрезков сохраняется, то точка Е – изображение точки Е0 – является серединой стороны АВ, а точка F лежит на стороне AD, причем AF:AD=1:4. Построим эти точки E и F, а также точку К, лежащую на прямой AD, такую, что точка D является серединой отрезка АК, и проведем прямую EF. Для построения искомой прямой х обратимся к выносному чертежу, на котором построим квадрат A0B0C 0D0 и заданные точки Е0 , F0 и К0 (рис. 17, б). Через точку К0 проведем прямую x0, перпендикулярную прямой Е0F0 . Пусть прямая x0 пересекает прямую Е0F0 в точке Н0 . На этом построение на выносном чертеже закончено. Возвратимся к рисунку 17, а. С помощью вспомогательного луча l с началом в точке Е построим на прямой EF точку Н, такую, что EF:EH= Е0F0 :Е0H0 (опорная задача 3), где отрезки Е0F 0 и Е0H0 взяты с рисунка 17, б. Прямая КН является изображением прямой x0. Вычислительный способ. Подсчитаем сторона треугольника EFK (рис. 17, в). Полагая, что сторона квадрата равна а, находим из треугольника AEF, где АЕ=½ а, AF=¼ a, EF2=AE2+AF2, EF=¼ а√5. 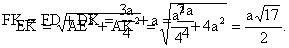 И из прямоугольного треугольника АЕК, где АЕ=½ а, АК=2а, находим: Если KH┴EF, то выполняется соотношение EK²-EH²=FK²- FH² (опорная задача 2), или И из прямоугольного треугольника АЕК, где АЕ=½ а, АК=2а, находим: Если KH┴EF, то выполняется соотношение EK²-EH²=FK²- FH² (опорная задача 2), или 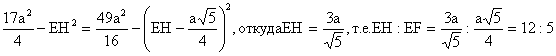 Выбрав произвольно единичный отрезок е, разделим отрезок EF в отношении EH:EF=p:q, где p=12e, q=5e (опорная задача 3). Получим точку Н и затем искомую прямую КН. 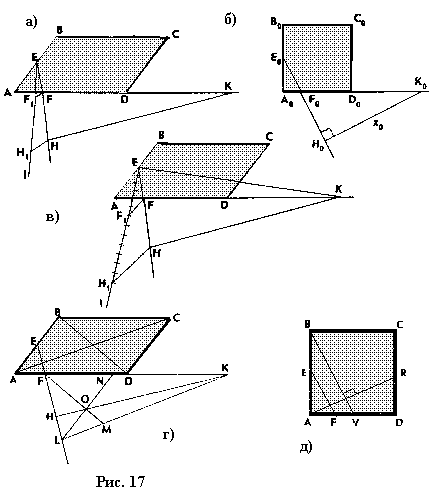 Геометрический способ (рис. 17, г). Так как параллелограмм ABCD является изображением квадрата, то прямые АС и BD являются изображением взаимно перпендикулярных прямых. Через точку К проведем прямую KL║AC. Через точку F проведем прямую FM║BD. Таким образом, в треугольнике KFL отрезок FM является изображением высоты. Через точку L проведем прямую LN║CD. Тогда в треугольнике KFL отрезок LN является изображением второй высоты. Найдем точку О, в которой пересекаются прямые FM и LN. Проведем прямую КО и найдем точку Н, в которой эта прямая пересекает прямую FL. Отрезок KН является изображением третьей высоты треугольника KFL, т. е. прямая КН – это изображение искомой прямой х0. Также можно доказать, что если в квадрате ABCD (рис.17, д) точки R и V – середины сторон соответственно CD и FD, то AR┴BV. Так как в рассмотренном примере EF║BV, то AR┴EF. Этим фактом можно воспользоваться для осуществления другого, также геометрического способа построения искомой прямой. 3.3. Построения на изображениях пространственных фигур.Построение прямой, перпендикулярной заданной прямой.Задача 5.Боковое ребро правильной призмы ABCDA1B1C1 D1 в два раза больше стороны ее основания. На ребрах АВ и ВB1 призмы заданы соответственно точки Р и В2 – середины этих ребер. Построить прямую, проходящую через точку Р перпендикулярно прямой В2 D. Решение. Способ выносных чертежей (рис. 18, а). Соединим точку Р с точками D и В2 . Построим треугольник, подобный оригиналу треугольника В2DР. Фигурой, подобной оригиналу грани ABCD, является квадрат A0B0 C0D0 (рис. 18, б). Отрезок D0P0 , где точка P0 – середина стороны A0B0 , примем за одну из сторон искомого треугольника. 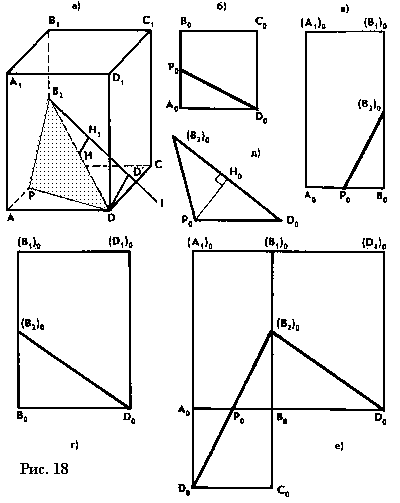 Фигурой, подобной оригиналу грани ABВ1А1, является прямоугольник A0B0(В1) 0(А1 )0 с отношением сторон A0B0: A0(А 1)0=1:2 (рис. 18, в). Причем его сторона A0B0 взята равной стороне квадрата, построенного на рисунке 18, б. Строим на сторонах A0B0 и B0(В1) 0 соответственно точки P0 и (В2) 0 – середины этих сторон. Отрезок P0(В2) 0 – это еще одна из сторон искомого треугольника. Строим прямоугольник B0(В1)0(D1) 0D0 (рис. 18, г), сторону B0(В1)0 которого возьмем с рисунка 18, в, а сторону B0D0 возьмем равной диагонали квадрата, построенного на рисунке 18, б. Отрезок (В2 )0D0 , где точка (В2)0 – середина стороны B0(В1)0 , - это третья сторона искомого треугольника. Строим треугольник P0(В2)0D0 по трем сторонам, найденным выше. В треугольнике P0(В2)0 D0 строим P0Н0┴(В2)0 D0 . Возвращаемся к рисунку 18, а. С помощью луча l, проведенного через точку В2 , строим точку Н, такую, что В2Н: В2D=(В 2)0H0:(В2)0D0 (опорная задача 3). Строим искомую прямую РН. Так как фигуры на рисунке 18 б, в, г, имеют общие стороны, то их можно объединить, например, так, как это показано на рисунке 18, е. 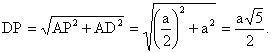 Вычислительный способ. Подсчитаем стороны треугольника PB2D (рис. 18, а). Для этого обозначим сторону основания призмы за а. Тогда ВВ1 =2а. Далее из прямоугольного треугольника ADP: Из прямоугольного треугольника РВВ2: 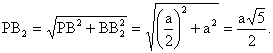 И из прямоугольного треугольника BB2D: 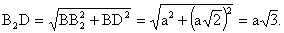 Если PH┴B2D, то выполняется соотношение (из опорной задачи 2). 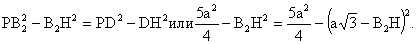 Откуда 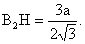 Тогда Тогда 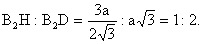 С помощью вспомогательного луча l строим на отрезке B2D точку Н, такую, что B2Н: B2D=1:2 (опорная задача 3). Строим искомую прямую РН. В некоторых случаях построение прямой, перпендикулярной данной, можно построить и геометрическим способом. С помощью вспомогательного луча l строим на отрезке B2D точку Н, такую, что B2Н: B2D=1:2 (опорная задача 3). Строим искомую прямую РН. В некоторых случаях построение прямой, перпендикулярной данной, можно построить и геометрическим способом.Геометрический способ. Ясно, что прямоугольные треугольники ADP и BB 2P равны (по двум катетам). Тогда DP=B2P, т. е. треугольник B 2DP – равнобедренный. Это значит, что медиана РН этого треугольника является и его высотой, т. е. прямая РН является искомой прямой. Построение прямой, перпендикулярной заданной плоскости.Один из возможных планов решения задачи о построении прямой, проходящей через заданную точку W перпендикулярно заданной плоскости α (рис. 19).1) В плоскости γ, определяемой точкой W и какой-нибудь прямой U 1U2 , лежащей в плоскостиα, проведем через точку W прямую т1 , перпендикулярную прямой U 1U2 . Пусть прямая т 1 пересекает прямую U 1U2 в точке V. 2) Проведем далее в плоскости α через точку V прямую т2 , перпендикулярную прямой U1U2 . 3) В плоскости β, определяемой прямыми т1 и т2 , построим прямую т3, проходящую через точку W перпендикулярно прямой т2 . Пусть прямая т3 пересекает прямую т2 в точке Н. Так как прямая U 1U2 пересекает прямые т1 и т 2 , то прямая U 1U2 перпендикулярна прямой т3 . Таким образом, прямая т3 перпендикулярна прямой U 1U2 и прямой т2 . Это значит, что прямая т3 перпендикулярна плоскости α , т. е. является искомой прямой. 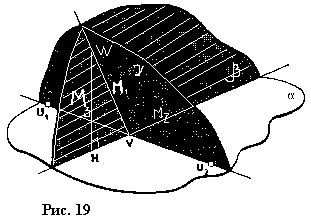 Задача 6. Высота МО правильной пирамиды МABCD равна стороне ее основания. Опустить перпендикуляр из вершины D на плоскость МВС. 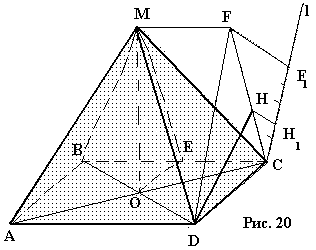 Решение (рис. 20). Выполним построение в соответствии с изложенном выше планом. Через точку D и прямую ВС плоскости МВС уже проходит плоскость γ – это плоскость DBC. В плоскости DBC уже проведена прямая DC┴ВС. Она пересекает прямую ВС в точке С. Чтобы в плоскости МВС (это плоскость α) провести через точку С прямую, перпендикулярную прямой ВС заметим, что в треугольнике МВС МВ=МС. Поэтому медиана МЕ будет и перпендикулярна к прямой ВС Таким образом, в плоскости МВС через точку С проведем прямую CF║МЕ. В плоскости β, определяемой прямыми DC и CF, из точки D опустим перпендикуляр на прямую CF. Сделаем это построение вычислительным способом . Подсчитаем стороны треугольника CDF, полагая CD = а. Из прямоугольного треугольника МОЕ: 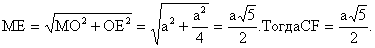 Ясно, что DF=CF (из равенства треугольников CMF и DMF). Если DH┴CF, то DC²-CH²=DF²-FH² (опорная задача 2). Так как DC<DF, то CH<FH. Таким образом, получаем уравнение: Ясно, что DF=CF (из равенства треугольников CMF и DMF). Если DH┴CF, то DC²-CH²=DF²-FH² (опорная задача 2). Так как DC<DF, то CH<FH. Таким образом, получаем уравнение: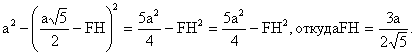 Следовательно, СН = а:√5 и тогда CH:CF = 2:5. Опираясь на это соотношение, построим на прямой CF точку Н (опорная задача 3) и затем искомый перпендикуляр DH. Построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости.Пусть заданы плоскость α и прямая т1. Если через какую-нибудь точку W прямой т1 провести прямуют 2, перпендикулярную плоскости α , то плоскость β, определяемая пересекающимися прямыми т1и т 2, будет перпендикулярна плоскости α Таким образом, задача построения плоскости β проходящей через заданную прямую т1 и перпендикулярной плоскости α, сводится к построению прямой т2, проходящей через какую-нибудь точку W прямой т1и перпендикулярной плоскости α Задача 7. На ребре CD правильной пирамиды MABCD, высота которой равна половине диагонали ее основания, взята точка Е – середина этого ребра и через точки M, B и Е проведена секущая плоскость α Построить сечение пирамиды плоскостью, проходящей через прямую BD перпендикулярно плоскости α Найти линию пересечения построенной плоскости с плоскостью α Решение (рис. 21, а). Опустим перпендикуляр из точки О – середины диагонали BD на плоскость α Построение этого перпендикуляра выполним с помощью выносных чертежей. 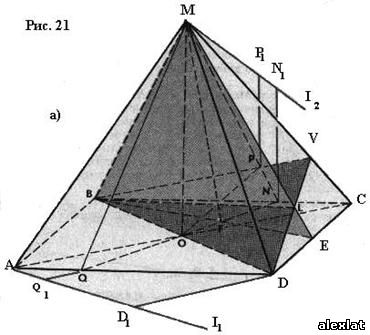 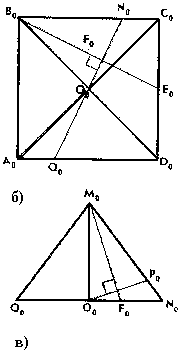 Построим квадрат A0B0C0D0 (рис. 21, б), точку О0, в которой пересекаются его диагонали, и проведем прямую B0Е0, где точка Е0 – середина стороны C 0D0 . Затем через точку О0 проведем прямую О0 Е0┴ B0Е0, и найдем точки О0 , N 0, в которых прямая О0 F0 пересекает соответственно прямые А0D0 и B0C0 . Вернемся к рисунку 21, а. С помощью луча l1 построим но отрезке AD точку Q, такую что AQ:AD=k1 А0Q0 : k1 А0D0 (опорная задача 3). Прямая QO является, таким образом, изображением прямой, перпендикулярной прямой ВЕ. Построим далее точки N и F, в которых прямая QO пересекает соответственно прямые ВС и ВЕ. Соединим точку М с точками Q, N и F. Построим теперь треугольник M0Q0N0 , подобный оригиналу треугольника MQN (рис. 21, в). Ясно, что в треугольнике M0 Q0N0 M0Q0=M0N0 . Сторону Q0N0 этого треугольника возьмем с рисунка 21, б вместе с точкой F0 , принадлежащей этому отрезку. Высоту М0 О0 возьмем равной отрезку А0О0 , полученному также на рисунке 21, б. В построенном треугольнике M0Q0N0 через точку О 0 проведем прямую, перпендикулярную прямой М0F0 , и точку пересечения построенной прямой с прямой M0N0 обозначим Р0. Вернемся к рисунку 21, а. С помощью луча l2 найдем точку Р, которая делит отрезок MN в отношении MP:MN= k0 M0 P0: k0 M0N0 (опорная задача 3). Точку О соединим с точкой Р. Прямыми BD и OP определяется плоскость искомого сечения. Строим сечение BVD и находим точку L, в которой пересекаются прямые DV и МЕ. Прямая BL – линия пересечения плоскости МВЕ с плоскостью BVD. Построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.Задача 8. В основании пирамиды МАВС лежит прямоугольный треугольник АВС, боковое ребро МС перпендикулярно плоскости основания, и отношение ребер СА:СВ:СМ=√2:√2:1. На ребрах соответственно точки D и Е – середины этих ребер. Построить сечение пирамиды плоскостью α, проходящей через точку Е перпендикулярно прямой МD. Решение. Способ выносных чертежей (рис. 22, а). Так как плоскость α перпендикулярна прямой МD, то прямая МD перпендикулярна любой прямой, лежащей в плоскости α. В частности, если прямая МD пересекает плоскость α в точке Н, то МD┴ЕН, т. е. отрезок ЕН – это высота треугольника М 0Е0D0, подобно оригиналу треугольника МЕD. 1) Построим равнобедренный прямоугольный треугольник А0В0 С0 (рис.22, б), точки D0 и Е0 – середины соответственно его сторон А0В0 и В0С0 , и таким образом получим отрезок D0Е0. Это одна из сторон треугольника М0Е0D0. 2) Построим прямоугольный треугольник В0С0М0 (рис. 22, в), катет В0С0 которого взят с рисунка 22, б. Из равенства СВ:СМ=√2:1 ясно, что катет С0М0 следует построить равным В0С0∙½√2 (т. е. он равен половине диагонали квадрата со стороной В0С0). Медиана М0Е0 треугольника В0С0М 0 – это вторая сторона треугольника М0Е0D0 . 3) Построим равнобедренный треугольник А0В0М0 (рис. 22, г), основание которого возьмем с рисунка 22, б, а боковые стороны А 0М0= В0М0 – с рисунка 22, в. Медиана М 0D0 треугольника А0В0М0 – это третья сторона треугольника М0Е0D0. 4) По трем полученным на рисунке 22, б, в, г сторонам строим треугольник М0Е0D (рис. 22, д) и проведем в нем Е0Н 0┴ М0D0. 5) Возвращаемся к рисунку 22, а. На рисунке 22, д точка Н0 разделила отрезок М0D0 в отношении М0Н0 : М0D0. С помощью луча l в таком же отношении разделим точкой Н отрезок МD (опорная задача 3). 6) Так как плоскость α и плоскость АВМ имеют общую точку Н то эти плоскости пересекаются по прямой, проходящей через точку Н Более того, так как прямая МD перпендикулярна плоскости α , то прямая МD перпендикулярна линии пересечения плоскостей α и АВМ. На рисунке 22. А уже есть прямая, которой прямая МD перпендикулярна. Это прямая АВ. (Действительно, в треугольнике АВМ АМ=ВМ, а МD – его медиана.) Поэтому, не обращаясь к новому выносному чертежу, проведем в плоскости АВМ через точку Н прямую FK║АВ. Теперь искомое сечение определяется точкой Е и прямой FK и нетрудно теперь построить, например, заметив, что, так как FK║АВ прямая FK параллельна плоскости АВС, а это значит, что плоскость α , проходящая через прямую FK, пересечет плоскость АВСпо прямой, параллельнойFK, т. е. по прямой ЕL║АВ. Таким образом, четырехугольник EFKL – искомое сечение. Треугольники А0В0С0, В0С0 М0 и А0В0М0 имеют равные стороны. Этим обстоятельством можно воспользоваться и объединить рисунки б, в, г в один рисунок, как это показано ни рисунке е. Вычислительный способ (рис. 22, а). Как и при решении способом выносных чертежей, будем строить ЕН┴МD. Для этого подсчитаем стороны треугольника MDE, введя для выполнения расчетов вспомогательный параметр, положив, например, МС=а. 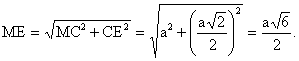 Тогда АС=ВС= а√2, и из прямоугольного треугольника АВС АВ=2а, следовательно, CD=a. Поэтому MD =a√2. Ясно, что DE=½AC=½ a√2, и из прямоугольного треугольника МСЕ Подсчитаем теперь отношение МН:MD. Если ЕН┴MD, то МЕ²- МН²=DE²-DH² (опорная задача 2), или 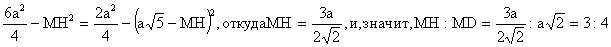 С помощью вспомогательного луча l строим точку Н (опорная задача3). Далее искомое сечение строится так, как это сделано способом выносных чертежей. 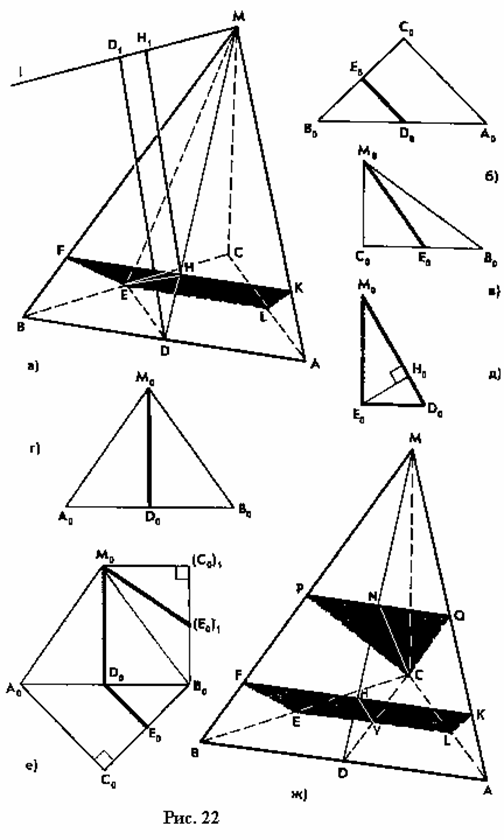 Глава IV. Вычисление расстояний и углов. 4.1. Расстояние от точки до прямой.Для определения расстояния от точки до прямой обычно рассматривают треугольник, одной из вершин которого является заданная точка, а две другие лежат на заданной прямой. Искомое расстояние находят как высоту этого треугольника , для чего в большинстве случаев подсчитывают сначала стороны треугольника. Вычисление сторон треугольника и затем его высоты выполняют поэтапно-вычислительным методом.Задача 9. В прямоугольном параллелепипеде ABCDA1B1C1 D1 АВ=АA1=а, AD=3a. На ребре A1B1 взята точка Р – середина этого ребра, а на ребре AD – точка Q, такая, что AQ:AD=2:3. Найти расстояние от вершины D1 до прямой PQ. Решение. (рис. 23). 1 способ. Подсчитаем стороны треугольника D1 PQ. Из прямоугольного треугольника D1DQ D1Q =a√2. Из прямоугольного треугольника A1D1P 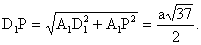 В плоскости АВB1 через точку Р проведем прямую РР’║AA1 и точку Р соединим с точкойQ. Из прямоугольного треугольника РР’Q: 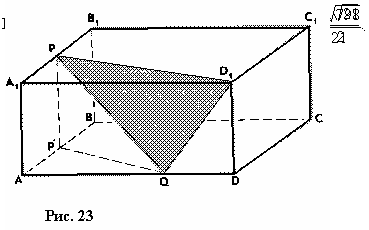 Если далее в треугольнике D1PQ D1H┴PQ, то Если далее в треугольнике D1PQ D1H┴PQ, то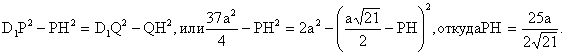 2 способ. Координатный метод решения (рис. 24). Введем в пространстве прямоугольную систему координат Bxyz, приняв за ее начало точку B, за единицу измерения отрезок, равный АB, а за координатные оси Bх, Bу и Bz соответственно прямые BА,BС и BB1 с направлением на них от точки B к точкам А, С и B Тогда в этой системе координат B(0; 0; 0), А(а; 0; 0), С(0;3а;0) и B1(0; 0; а). 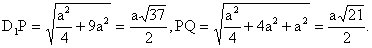 Найдем координаты точек D1, Рисунка и Q Получаем D1 (а; 3а; а), P(½а; 0; а) и Q (а; 2а; 0). 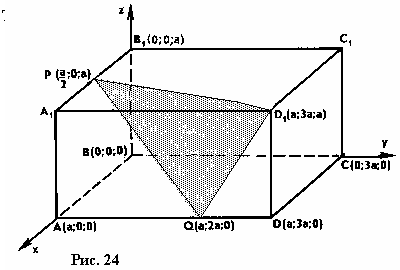 Теперь подсчитаем cos D1PQ. По теореме косинусов получаем Это и есть искомое расстояние. Теперь подсчитаем cos D1PQ. По теореме косинусов получаем Это и есть искомое расстояние.4.2. Расстояние от точки до плоскости.Можно предложить следующий план нахождения расстояния от заданной точки W до заданной плоскости α поэтапно-вычислительным методом:1. Построим плоскость β, проходящую через точку W перпендикулярно какой-нибудь прямой m1, лежащей в плоскости α. 2. Найдем прямую m2 – линию пересечения плоскостей β и α. 3. Выберем на прямой m2 какие-нибудь две точки U и Т и подсчитаем высоту WH треугольника WUT. Так как прямая m1 перпендикулярна плоскостиβ, то она перпендикулярна любой прямой, лежащей в плоскости β, и, в частности, m1┴WH. Таким образом, WH┴ m1 и WН┴ m 2, т. е. прямая WН перпендикулярна плоскости α, и, значит, WH – искомое расстояние. Задача 10. В заданном прямоугольном параллелепипеде ABCDA1B1 C1D1 с соотношением ребер АВ:АD:АA1=1:2:1 точка Р- середина ребра АA1. Найти расстояние от вершины D1 до плоскости В1DР, считая АВ=а. Решение (рис. 25). Находим прямую S1S2 – след плоскости B 1DP на плоскости A1B1C1 и строим сечение параллелепипеда заданной плоскостью B1DP. Проведем решение в соответствии с предложенным выше планом. 1. Построим плоскость β, проходящую через точку D1 перпендикулярно, например, прямой S1S2 , лежащей в плоскости B1DP. Одна прямая, проходящая через точку D1 и перпендикулярная прямой S1S2 , на изображении уже есть – это прямая DD1. Для построения второй прямой подсчитаем стороны прямоугольного треугольника D1S1S2 . Ясно, что D1S1=2D1А1=4а, D1S2 =2D1С1=2а, и тогда 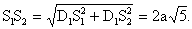 Если D1L┴ S1S2, то в треугольнике D1 S1S2 D1S12 = S1 L∙ S1S2, откуда Если D1L┴ S1S2, то в треугольнике D1 S1S2 D1S12 = S1 L∙ S1S2, откуда 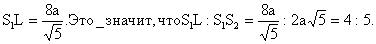 Таким образом, точка L может быть построена с помощью вспомогательного луча l. Прямыми D1D и D1L определяется плоскость β. 2. Найдем прямую, по которой пересекаются плоскости β и B1 DP. Так как точки D и L – общие точки этих плоскостей, то прямая DL – линия их пересечения. 3.  Подсчитаем расстояние от точки D1 до прямой DL. Если D1Н – высота треугольника D1DL, то выражая площадь этого треугольника двумя способами, получим: D1H∙DL= DD1∙ D 1L, ,
 | |||
| Просмотров: 3942 | Комментарии: 1 | | |||
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта