Введение.
Выбранная для реферата тема «Решение задач с помощью ортогонального
проектирования» актуальна для многих выпускников и поступающих в высшие
учебные заведения.
Несмотря на то, что в методических рекомендациях по решению экзаменационных
задач по геометрии говорится, что для них не требуется сложных рассуждений,
преобразований и остроумия, но часто приобретенных навыков в школе не хватает
для решения задач на построение и вычислительных задач. Многие из них на
сегодняшний день полностью отсутствуют или редко встречаются в учебниках. Это
относится в первую очередь к заданиям на применение ортогонального
проецирования.
Рассмотренный в данном реферате материал позволяет получить более глубокие
знания по стереометрии, широкое понимание поставленного вопроса. Особое
внимание уделено полноте рассуждения, в котором применялись базовые знания
начертательной геометрии. При решении задач активно использовался аппарат
ортогонального проектирования. Это осуществляется применением вычислительного
способа и способа выносных чертежей. В реферате также присутствует и
координатный способ решения. Акцентируется внимание на решении задач по
построению прямой, изображений фигур, вычислению расстояний и углов.
Глава I. Основные понятия ортогональной
проекции. Комплексные чертежи.
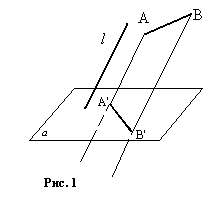
Дана плоскость α и прямая l , задающая направление проецирования.
Зададим фигуру, которую надо спроектировать (отрезок AB). Через точки А и В
проведем прямые, параллельные l и пересекающие плоскость α в
точках A’, B’. Отрезок A’ B’ – проекция АВ на плоскость α (рис.1).
Обозначается A’ B’ =пр α AB.
Свойства параллельной проекции.
1) Проекцией точки является точка.
2) Проекцией прямой является прямая – свойство прямолинейности.
3) Проекцией точки, лежащей на некоторой прямой, является точка, лежащая
на проекции данной прямой – свойство принадлежности.
4) Проекциями параллельных прямых являются параллельные прямые –
свойство сохранения параллельности.
5) Отношение проекций отрезков, лежащих на параллельных прямых или на
одной и той же прямой, равно отношению самих отрезков.
6) Проекция фигуры не меняется при параллельном переносе плоскости
проекций.
Ортогональное проецирование является частным случаем параллельного
проецирования, когда направление проецирования S перпендикулярно плоскости
проекции П’.
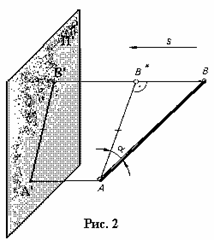
В этом случае нетрудно установить соотношение между длиной натурального
отрезка и длиной его проекции. Если отрезок AB образует с плоскостью проекций
угол α, то, проведя AB*║A’ B’ (рис.2), получим из прямоугольного
треугольника AB*B, что AB*=AB cos α или A’ B’= AB cos α.
Так как ортогональное проецирование – разновидность параллельного, то ему
присущи те же свойства.
Наибольшее применение получил чертеж, составленный из двух или более
связанных между собой ортогональных проекций изображаемого оригинала. Такой
чертеж называется комплексным.
Принцип образования такого чертежа состоит в том, что данный оригинал
проецируется ортогонально на две взаимно перпендикулярные плоскости проекций,
которые затем соответствующим образом совмещают с плоскостью чертежа. Одна из
плоскостей проекции П1 располагается горизонтально и называется
горизонтальной плоскостью проекций. Плоскость П2 , которая
располагается вертикально, называется фронтальной плоскостью проекций
(рис. 3).
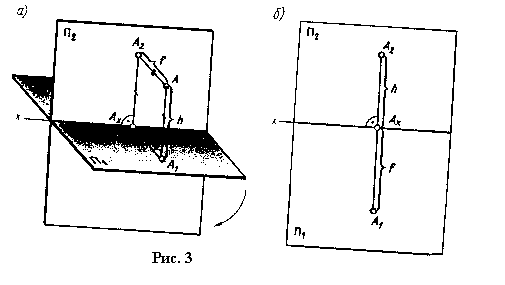
Прямую пересечения плоскостей проекций называют осью проекций.
Спроектируем ортогонально на плоскости проекций П1 и П2
какую-нибудь точку А, тогда получим две ее проекции: горизонтальную проекцию
А1 на плоскости П1 и фронтальную проекцию А2
на плоскости П2 .
Проектирующие прямые АА1 и АА2 , при проекции которых
точка А проектируется на плоскости проекций, определяют проецирующую плоскость
А1АА2 , перпендикулярную к обеим плоскостям проекций и к
оси проекций х. Прямые Ах А1 и Ах А
2 , являющиеся проекциями проецирующей плоскости на плоскостях проекций П
1 и П2 , будут перпендикулярны к оси проекций х.
Расстояние А1А точки А от горизонтальной плоскости проекций
называется высотой h точки А, ее расстояние А2А от
фронтальной плоскости проекций – глубиной f точки А.
Чтобы получить плоский чертеж, совместим плоскость проекций П1 с
плоскостью П2 , вращая плоскость П1 вокруг оси х
в направлении, указанном на рис. 3, а. В результате получим комплексный
чертеж точки А (рис. 3, б), состоящий из двух проекций А1 и А
2 точки А, лежащих на одной прямой, перпендикулярной к оси х.
Прямая А1А2 , соединяющая две проекции точки, называется
линией связи.
Прямая линия определяется двумя точками, поэтому на комплексном чертеже всякая
прямая l может быть задана проекциями А1 , А2 и В
1 , В2 двух ее точек А и В (рис. 4, а, б). А так как
ортогональная проекция обладает свойствами прямолинейности и принадлежности, то
прямая l на комплексном чертеже задается и ее проекциями l
1 , l2; они будут прямыми, проходящими через точки А
1 , В1 , А2 , В2.
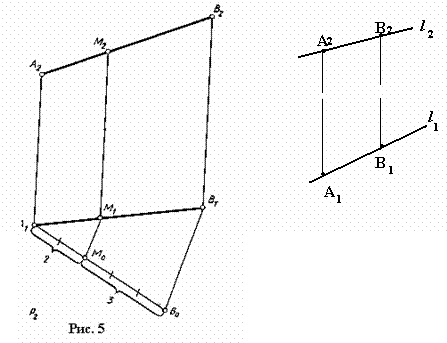
Для деления данного отрезка АВ в данном отношении достаточно разделить в этом
отношении одну из проекций данного отрезка, а затем спроецировать делящую
точку на другую проекцию отрезка. На рис. 5 отрезок АВ разделен точкой М в
отношении 2:3, первоначально в этом отношении была разделена проекция А1
В1 данного отрезка.
Определение натуральной величины отрезка прямой и его углов наклона к
плоскостям проекций можно выполнить с помощью способа прямоугольного
треугольника. Пусть дан отрезок АВ общего положения (рис. 6, а).
Зафиксируем плоскость проекций П1 так, чтобы она прошла через один
из концов отрезка, например через точку А, и из точки В восстановим
перпендикуляр ВВ1. Тогда получим прямоугольный треугольник АВ1
В, в котором гипотенузой является данный отрезок АВ, одним катетом является
горизонтальная проекция А1В1 отрезка АВ, а вторым катетом
– высота h точки В. Угол, образованный отрезком АВ и его проекцией А
1В1 , является углом наклона отрезка АВ к плоскости проекций П
1 .
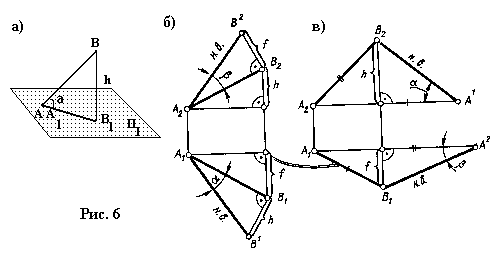
На рис. 6, б выполнено построение натуральной величины отрезка АВ, заданного
своими проекциями А1В1 и А2В2 , при
этом возможны два варианта решения. В одном случае построен прямоугольный
треугольник А1В1В1 на горизонтальной проекции
данного отрезка, а в другом - прямоугольный треугольник А1В1
В2 на фронтальной проекции отрезка. Гипотенузы этих треугольников А
1В1 и А2В2 определяют натуральную
величину отрезка АВ, а углы α и β определяют углы наклона этого
отрезка к плоскостям проекций П1 и П2 . Иногда удобнее
строить прямоугольный треугольник не на проекции отрезка, а на высоте h
или на глубине f одного из концов отрезка относительно другого. На рис.
6, в показаны оба варианта этих построений. Отрезки А1 В2
и А2 В1 определяют натуральную величину отрезка АВ.
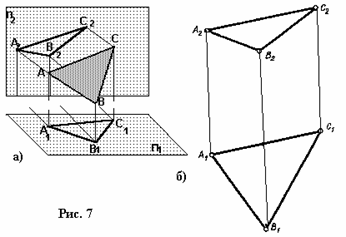
Плоскость определяют три ее точки, не лежащие на одной прямой. Поэтому на
комплексном чертеже всякая плоскость Q может быть задана проекциями А1
, В1 , С1 и А2 , В2 , С2
трех ее точек А, В, С (рис. 7 а, б). Для большей наглядности соединим точки А, В
и С прямыми. Получим задание плоскости треугольником АВС. При этом следует
помнить, что плоскость безгранична и поэтому некоторые построения могут
выходить за пределы треугольника.
Покажем, как задать какую-нибудь точку плоскости. Пусть плоскость Q задана тремя
точками А, В и С (рис. 8). Соединим их прямыми, тогда плоскость Q будет задана
треугольником АВС. Проще всего искомую точку М1 задать на
какой-нибудь стороне, например ВС. Проведем в плоскости Q произвольную прямую
l. Выделим на плоскости Q две произвольные точки, например, А и М1
, и определим этими точками прямую l (l1 ,l2),
принадлежащую плоскости Q.
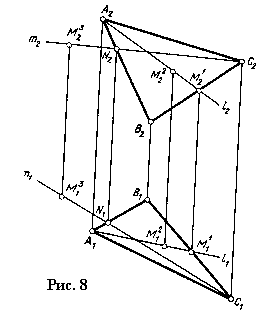
Так как проекция плоскости Q покрывает все поле проекций, то одну из проекций
точки, принадлежащей плоскости, можно задать произвольно, тогда вторая проекция
определится однозначно. Выберем произвольно проекцию М13
. Далее проведем в плоскости Q какую-нибудь прямую m, горизонтальная
проекция которой проходила бы через выбранную проекцию М13
. Прямая m определена точками C и N, принадлежащими плоскости Q.
Построив вторую проекцию m2 прямой m в пересечении с
линией связи, проведенной через М13 ,найдем искомую
проекцию М13 .
Таким образом, построение точки в данной плоскости сводится к двум операциям:
построению в плоскости вспомогательной прямой и построению точки на этой
прямой.
Глава II. Изображение фигур.
Изображаемая фигура называется оригиналом, а изображенная –
проекцией данной фигуры.
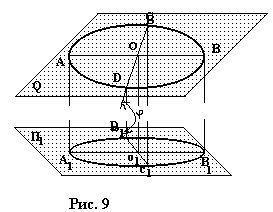
Параллельной проекцией окружности является кривая, называемая эллипсом. Так как
ортогональная проекция является частным случаем параллельной проекции, то,
проецируя окружность О, расположенную в плоскости общего положения Q (рис. 9)
ортогонально на плоскость П1 , получаем эллипс О1 .
В окружности проведем два взаимно перпендикулярных диаметра АВ и CD, причем АВ
пройдет по прямой уровня плоскости Q, а диаметр CD – по прямой наибольшего
уклона этой плоскости по отношению к плоскости проекций П1. Тогда
диаметр АВ спроецируется в диаметр А1В1 эллипса, равный
диаметру окружности, т.е. АВ=А1В1 , а диаметр CD
спроецируется в диаметр C1D1 эллипса. Так как угол,
образованный этими диаметрами, является линейным углом двугранного угла наклона
плоскости Q к плоскости П1 , то, обозначив его через φ, получим
C1D1=CD cosφ. Взаимно перпендикулярные окружности
диаметры обладают свойством сопряженности (каждый сопряженный диаметр делит
пополам хорды, параллельные другому диаметру). Это свойство при параллельном
проецировании сохраняется. Следовательно, диаметры А1В1 и
C1D1 будут сопряженными диаметрами эллипса. Но, с другой
стороны, они взаимно перпендикулярны, поэтому являются осями эллипса, причем А
1В1- большая ось, а C1D1- малая ось.
Треугольник изображается треугольником любой формы. Медиана треугольника
будет изображаться медианой, так как отношение отрезков сохраняется. При
проекции биссектрисы и высоты пойдет искажение.
Так как параллельность прямых сохраняется, то изображение параллелограмма, в
частности, прямоугольника, ромба, квадрата, служит параллелограмм. Длина
сторон и величины углов произвольные.
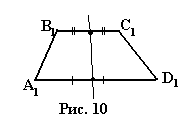
Любая трапеция изображается в виде произвольной трапеции. Сохраняется только
отношение оснований. Равнобокая трапеция имеет ось симметрии. Ее изображают
следующим образом (рис. 10). Каждое из оснований делим пополам и проводим ось
симметрии.
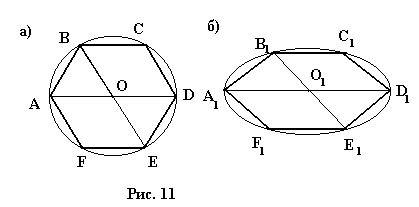
При построении оригинала правильного шестиугольника используют два
симметричных ромба: OBCD и OAFE (рис. 11, а). Изображение же получается при
построении ромбов в виде двух одинаковых произвольных параллелограммов. Для
получения проекции правильного шестиугольника надо оставшиеся точки соединить
(рис. 11, б).
Тетраэдр (треугольная пирамида) изображается в виде произвольного
четырехугольника с его диагоналями (рис.12, а).
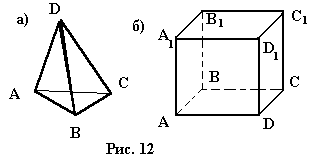
Для построения проекции параллепипеда сначала из произвольной точки проводим
три луча различной длины, не совпадающие. Затем на каждой паре лучей строим
параллелограмм. Полученный каркас достраиваем до параллепипеда (рис. 12,б).
Глава III. Задачи на метрические построения.
Чертеж, на котором построена фигура Ф0 , имеющая форму оригинала
заданной плоской фигуры (т. е. подобная фигуре Ф), называют выносным
чертежом фигуры Ф.
Если точки P, Q и R принадлежат секущей плоскости и не лежат на одной прямой, а
их проекции на плоскость, выбранную в качестве основной, - точки P’, Q’ и R’,
то точки пересечения соответственных прямых, т.е. точки S1
=PQ∩P’Q’, S2=PR∩P’R’, S3=RQ∩R’Q’, лежат
на одной прямой. Эта прямая является основным следом секущей плоскости.
Построение выносных чертежей может быть выполнено вычислительным, а
также геометрическим способом.
Задача 1. На ребрах ВВ1 и CD куба ABCDA1B1C
1D1 взяты соответственно точки P и Q – середины этих ребер.
Построить фигуру, подобную многоугольнику, полученному в сечении кубу
плоскостью С1PQ.
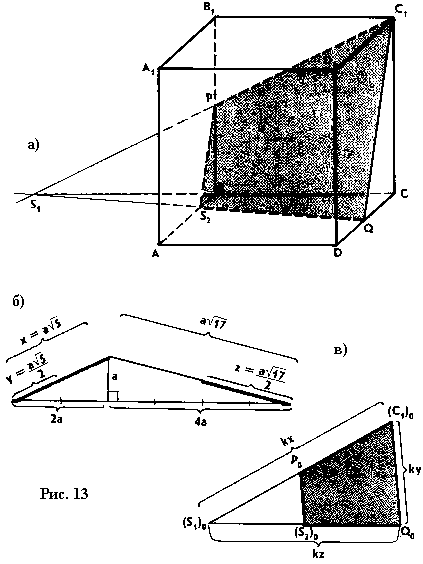
Решение (рис. 13, а). Находим точку S1 , в которой пересекаются
прямые C1P и BC. Таким образом, прямая S1Q является
основным следом плоскости C1PQ, а в сечении получается
четырехугольник C1PS1Q.
I способ построения – вычислительный. Полагая ребро куба равным a
, подсчитаем стороны треугольника C1S1Q. Как нетрудно
показать, точка Р – середина отрезка C1S1 и PS2
║ C1Q. Поэтому ясно, что, построив треугольник, подобный
оригиналу треугольника C1S1Q, можно будет затем построить
и искомую фигуру.
Из прямоугольного треугольника C1S1С, в котором C1
S=2ВС=2a, находим, что C1S1=a√5. Затем
из прямоугольного треугольника C1СQ получаем C1Q=½
a√5 и из прямоугольного треугольника CS1Q: S1
Q=½ a√17.
Выбирая теперь некоторый отрезок в качестве отрезка, равного а, построим
отрезки x, y, z, заданные следующими формулами: x= a√5 ,
y=½ a√5, z=½ a√17,
например, так, как это сделано ни рисунке 13, б.
Далее на рисунке13, в строим треугольник (С1)0Q0
(S1)0 со сторонами (С1)0(S1
)0 =kx, (S1)0Q0=kz,
полученными на рисунке13, б.
Строим затем точку P0 – середину стороны (C1)0
(S1)0 этого треугольника и проводим через нее прямую P
0(S1)0║(C1)0Q0
. Четырехугольник (С1)0Q0(S2)0
P0 – фигура, подобная заданному сечению куба плоскостью C1
РQ (т. е. это выносной чертеж многоугольника, являющегося сечением куба
плоскостью C1РQ).
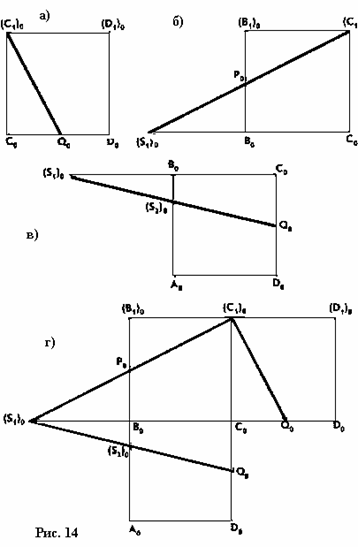
II способ – геометрический. Так как все квадраты подобны между собой, то
квадрат (С1)0С0D0(D1)
0 (рис. 14, а) подобен оригиналу грани C1CDD1 куба.
Построив на этом изображении точку Q0 – середину стороны C0
D0 и соединив точки (С1)0 и Q0 ,
получим отрезок (С1)0Q0 , который можно
принять за сторону треугольника (С1)0Q0(S
1)0 , подобного оригиналу треугольника C1QS1
. С помощью квадрата (С1)0C0B0(B
1)0 (рис. 14, б), равного квадрату (С1)0C
0D0(D1)0 , построенному на рисунке 14, а,
строим отрезок (С1)0(S1)0 , который
будет принят за сторону треугольника (С1)0Q0
(S1)0 , подобно оригиналу треугольника C1QS
1.
С помощью квадрата A0B0C0D0 (рис.
14, в), равного квадрату, построенному на рисунке 14, а, строим отрезок (S
1)0Q0 , который примем за третью сторону
треугольника (С1)0Q0(S1)0
. Получив, таким образом, все стороны треугольника (С1)0
Q0(S1)0 , строим этот треугольник. Далее, как и
при вычислительном способе решения, строим точку Р0 – середину
стороны (S1)0(C1)0 и т. д.
Рисунки а, б, в можно объединить в один рисунок, например, в рисунок г. Так как
треугольник (С1)0Q0(S1)0
строится с точностью до подобия, то его сторонами являются отрезки, равные k
(С1)0(S1)0 , k(С1
)0Q0 и k(S1)0Q0 ,
где k>0, например, k=1.
|