| Главная » Статьи » Математика » Геометрия в пространстве |
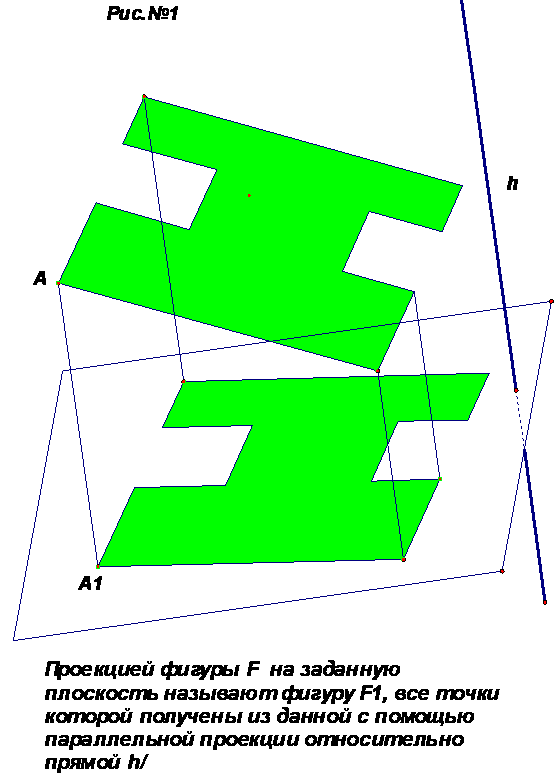
Изображение пространственных фигур на плоскости Для изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием (в черчении говорят «проецированием»). Этот способ изображения фигур состоит в следующем: берём произвольную прямую «h», пересекающую плоскость чертежа «α», проводим через произвольную точку А фигуры прямую, параллельную прямой «h.» Точка А1 пересечения этой прямой с плоскостью чертежа будет изображением точки А (см. рис.1)
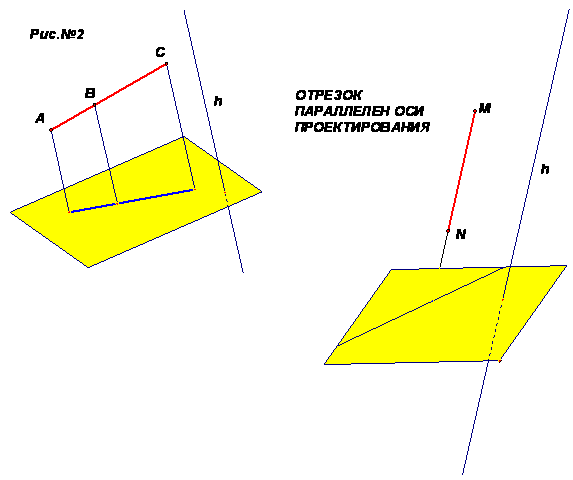
Построим, таким образом, изображение каждой точки фигуры, получим изображение самой фигуры. Такой способ изображения пространственной фигуры на плоскости соответствует зрительному восприятию фигуры, при рассмотрении её издали. Уточняющий вопрос к объяснению: Может ли прямая, проведённая через точку А параллельно прямой «h» , не пересечь плоскость «α»? Ответ: обязательно пересечёт, т.к. если плоскость пересекает одну из двух параллельных прямых, то она пересекает и другую. Свойства параллельного проектирования. I свойство: Вопрос: 1)Чем может быть изображён отрезок на плоскости? Ответ: отрезком. 2)Какой фигурой может оказаться параллельная проекция отрезка? Ответ: отрезком или точкой, если этот отрезок параллелен прямой проектирования «h». Показать рис.2
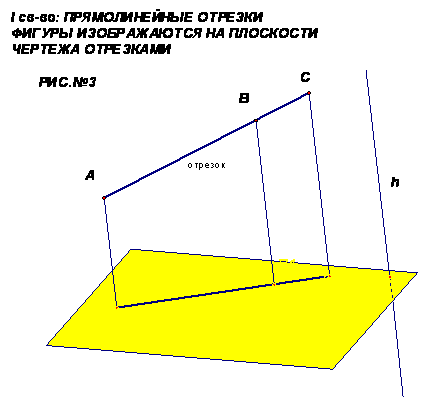
•Таким образом: прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками (см. рис2) Действительно, все прямые, проектирующие точки отрезка АС, лежат в одной плоскости, пересекающей плоскость чертежа «α» по прямой А1С1. Произвольная точка В отрезка АС изображается точкой В1 отрезка А1С1.(рис.№3)
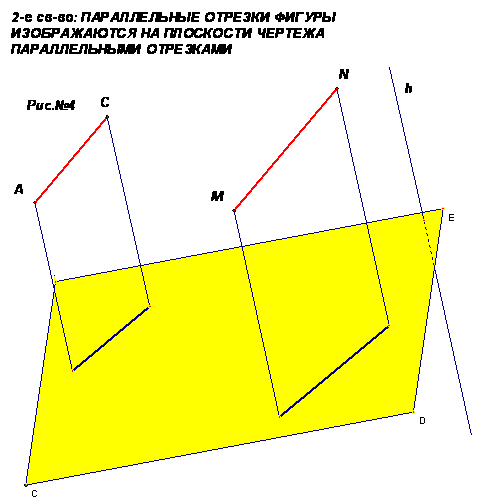
Замечание. В только что доказанном свойстве и далее предполагается, что, конечно, что проектируемые отрезки не параллельны направлению проектирования. То есть мы показали, что проекцией каждой точки отрезка АС является точка отрезка А1С1. Следствие I свойства: Многогранники ( плоские или пространственные) изображаются на плоскости чертежа многогранниками (или, в исключительных случаях, отрезками) Вопрос: 1)Может ли при параллельном проектировании многоугольника получиться многоугольник с меньшим числом сторон? Ответ: Да, если многоугольник пространственный. Для плоских многоугольников ответ отрицательный (нет). II свойство: Вопрос: Как изобразятся при параллельном проектировании параллельные прямые (отрезки). Ответ: параллельными или совпадающими прямыми (параллельными или лежащими на одной прямой отрез • Параллельные отрезки фигуры изображаются на плоскости чертежа параллельными отрезками (см. рис4)
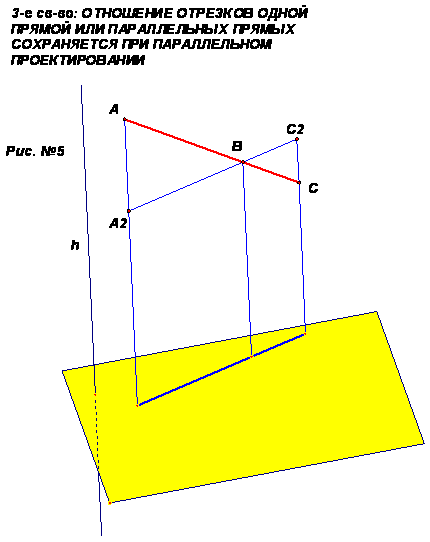
Действительно, пусть АС ║ А′С′. Прямые А1С1 ║ А′1С′1 т.к. они получаются при пересечении параллельных плоскостей с плоскостью «α». Первая проходит через АС и АА1 , вторая через А′С′ и А′А′1 . Вопрос: Почему указанные плоскости параллельны? (если две параллельные плоскости параллельны, то линии их пересечения параллельны) Задача: Может ли при параллельном проектировании параллелограмма получиться трапеция? Ответ; не может. Так как при параллельном проектировании параллельные прямые изображаются параллельными, то параллельной проекцией параллелограмма будет параллелограмм (или отрезок). III свойство: 1)Сохраняются ли длины отрезков при параллельном проектировании? (если отрезки параллельны плоскости, то сохраняются). 2)Сохраняются ли отношения длин? Так как мы уже достаточно поработали устно, то для доказательства третьего свойства сделаем чертёж(см. рис.№5).
• Отношение отрезков одной прямой или параллельных прямых сохраняются при параллельном проектировании. Рассмотреть доказательство третьего свойства по чертежу. Дано: отрезок АС, который разделён точкой В в отношении 2:1 (считая от точки А). Доказать, что проекция отрезка А1 С1 делится точкой В1 в отношении 2:1 (считая от точки А1) Доказательство Покажем, что АВ А1В1 ВС В1С1 Проведем А2С2 ║ А1С1 (по построению) ; ▲АВА2 ∞ ▲ СВС2 (по двум углам) Так как А1А2 ВВ1 и В1ВС2С1 являются параллелограммами (по определению), то А1В1 = А2В и В1С1 = ВС2 АВ А2В АВ А1В1 ВС ВС2 т.е. ВС В1С1 А теперь рассмотрим задачу по готовому чертежу. Задача Дана параллельная проекция треугольника. Как построить проекции медиан этого треугольника Решение. При параллельном проектировании сохраняется отношение отрезков прямой, поэтому, середина стороны треугольника проектируется в середину проекции этой стороны. Следовательно, проекции медиан треугольника будут медианами его проекций. Эта задача имеет довольно неожиданное применение. Очевидно, в правильном (равностороннем) треугольнике медианы пересекаются в одной точке – в центре треугольника. Но произвольный треугольник АВС можно спроектировать в правильный треугольник АВС1 (см. рис).Достаточно построить такой правильный треугольник АВС1 в плоскости, не проходящей через точку С и проектировать параллельно прямой h = СС1 Рассматривая эту проекцию видим, что медианы любого треугольника пересекаются в одной точке. Задача Докажите, что параллельная проекция центрально - симметричной фигуры также является центрально – симметричной. Назвать известные центрально симметричные фигуры. Ответ: квадрат, окружность, круг. Решение Так как при параллельном проектировании середина отрезка переходит в середину его проекции, проекция центра симметрии фигуры будет являться центром симметрии проекции этой фигуры. (см. рис) Параллельная проекция фигуры | |
| Просмотров: 12214 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |