| Главная » Статьи » Математика » Интегралы |
ИНТЕГРАЛ
ИНТЕГРАЛ (от лат. integer-целый), одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным (напр., находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т. п. Соответственно с этим различают неопределённые и определённые И., вычисление к-рых является задачей интегрального исчисления. Неопределённый интеграл. Первообразная функции f(x) одного действительного переменного - функция F(x)<, производная к-рой при каждом значении х равна f(x). Прибавляя постоянную к первообразной к.-л. функции, вновь получают первообразную той же функции. Следовательно, имея одну первообразную F(X) функции f(x), получают общее выражение всех первообразных этой функции в виде F(X) + С. Это общее выражение первообразных называют неопределённым интегралом: ∫f(x)sx функции f(x). Одна из основных теорем интегрального исчисления устанавливает, что каждая непрерывная функция f(x) действительного переменного имеет неопределённый И. Определённый интеграл. Определённый И. функции fix) с нижним пределом а и верхним пределом Ь можно определить как разность 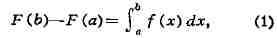 где F(X) есть первообразная функции f(x); определение не зависит от того, какая из первообразных выбрана для вычисления определённого И. Если функция f(x) непрерывна, то приведённое определение в случае а<b равносильно следующему определению, данному О. Каши (1823): рассматривают произвольное разбиение отрезка [a,b] точками α = x0<x1<...<xn = b; (2) в каждом отрезке ℇ1(x1-1≤ℇ1≤x1) [xи образуют сумму 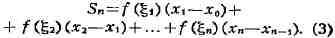 Сумма S зависит от выбора точек x. Однако в случае непрерывной функции f(x) суммы Sпри различном выборе точек x, стремятся к вполне определённому пределу, если максимальная из разностей x . Этот предел и является определённым интегралом 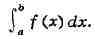 По определению, 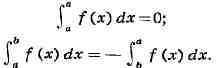 Определённый И., как указано выше,< выражается через любую первообразную F(X). Обратно, первообразная F(x) может быть записана в виде 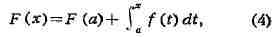 где а - произвольная постоянная. В соответствии с этим неопределённый И. записывается в виде 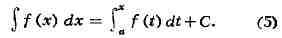 О возникновении понятия И., а также о свойствах неопределённых и определённых И. см. Интегральное исчисление. Обобщение понятия интеграла Интеграл Римана. О. Коши применял своё определение И. только к непрерывным функциям. Назвать, по определению, интегралом 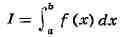 (6) (6) предел сумм S во всех тех случаях, когда этот предел однозначно определён, предложил Б. Римом. (1853). Он же исследовал условия применимости такого определения. Более совершенную форму этим условиям придал А. Лебег (1902), пользуясь введённым им понятием меры множества (см. Меры теория). Для интегрируемости в смысле Римана функции f(x) на [а,b] является необходимой и достаточной совокупность двух условий: f(x) ограничена на [а,b]; множество помещающихся на [а,b] точек разрыва функции f(x) имеет меру, равную нулю. T. о., непрерывность в каждой точке отрезка [а,b] совсем не обязательна для интегрируемости по Риману. Неопределённый И. и первообразную можно теперь определять формулами (5) и (4). Следует только заметить, что при этом первообразная F(X) не обязана иметь подинтегральную функцию f(x) своей производной в каждой точке. Но в каждой точке непрерывности f(x), т. е., в силу результата Лебега, всюду, кроме, может быть, множества меры, равной нулю, будет d/dxF(x)= f(x) (7) Г. Дарбу (1879) дал определение интеграла Римана, к-рое делает особенно наглядными условиями существования такого И. Вместо сумм (3) Дарбу вводит суммы 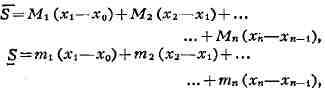 (наз. суммами Дарбу) (наз. суммами Дарбу) где Mверхняя грань функции f(x) нa отрезке [xa m нижняя грань сумм S, I , а - верхняя грань сумм S то для существования интеграла Римана необходимо и достаточно условие I=I Общее значение I = I = I величин _ I и I и является I и I интегралом Римана (6). Сами величины называются верхним и, соответственно, нижним интегралами Дарбу. Интеграл Лебега. Введённое Лебегом понятие меры множества позволило дать значительно более широкое определение И. Чтобы определить И. (6), Лебег делит точками ...<y-2<y-1<y0<Y1<...<y1... область возможных значений переменного у = f(x) и обозначает Mточек x из отрезка [a,b], для к-рых t1-1≤f(x)<y1 Сумма S определяется равенством 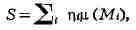 где 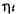 берётся из отрезка берётся из отрезка 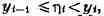 а Ii(Mt) а Ii(Mt) обозначает меру множества Mt. Функция f(x) называется интегрируемой в смысле Лебега на отрезке [а,b], если ряды, определяющие суммы S, абсолютно сходятся при max 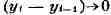 . Предел этих сумм и называется интегралом Лебега (6). .Можно определить первообразную в смысле . Предел этих сумм и называется интегралом Лебега (6). .Можно определить первообразную в смысле Лебега как функцию F(X), удовлетворяющую равенству (4), где И. в правой части понимается по Лебегу. Как и в случае интеграла Римана, равенство (7) 45удет при этом выполняться во всех точках, кроме, может быть, множества, имеющего меру, равную нулю. Для интегрируемости по Лебегу ограниченной функции f(x) необходимо и достаточно, чтобы она принадлежала к числу измеримых функций в смысле Лебега. Все функции, встречающиеся в матем. анализе, измеримы в этом смысле. Более того, до настоящего времени (1972) не построено ни одного индивидуального примера неизмеримой функции. T. о., для случая ограниченных функций Лебег решил задачу определения интеграла (6) с общностью, исчерпывающей потребности матем. анализа. Среди функций, интегрируемых по Лебегу, имеется сколько угодно функций, всюду разрывных и, следовательно, неинтегрируемых по Риману. Наоборот, каждая интегрируемая по Риману функция интегрируема и по Лебегу. Определение Лебега обобщается на случай интегрирования по полупрямой и по полной прямой, т. е. на случай И. вида 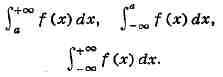 После этого обобщения теория Лебега охватывает все случаи абсолютно сходящихся несобственных интегралов. Общность, достигнутая в определении Лебега, весьма существенна во многих вопросах математич. анализа; напр., только с введением интеграла Лебега могла быть установлена теорема Фишера - Риса в теории тригонометрия, рядов, в силу к-рой любой ряд 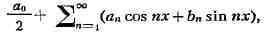 для к-рого 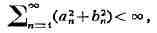 представляет функциюf(x), порождающую коэффициенты aформулам 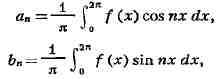 где И. понимаются в смысле Лебега. Интеграл Стилтьеса. В кон. 19 в. определение интеграла Римана подверглось совершенно иному обобщению, чем то, к к-рому привело введение понятия меры множества. Это обобщение было дано T. Стилтьесом (1894). Пусть f(x)- непрерывная функция действительного переменного х, определённая на отрезке [а,Ь], и U(x)- определённая на том же отрезке ограниченная монотонная (неубывающая или невозрастающая) функция. Для определения интеграла Стилтьеса берут произвольное разбиение (2) отрезка [а,b] и составляют сумму 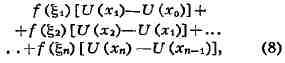 где ℇ1,ℇ2,...ℇn - произвольные точки, выбранные соответственно на отрезках [x[x- наибольшее расстояние между двумя последовательными точками деления в разбиении (2). Если взять любую последовательность разбиений, для к-рой S стремится к нулю, то сумма (8) будет иметь определённый, всегда один и тот же предел, как бы ни выбирались точки<...,на соответствующих отрезках. Этот предел называют, следуя Стилтьесу, интегралом функции f(x) относительно функции U(x) и обозначают символом 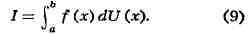 Интеграл (9) (его называют также и н-тегралом Стилтьеса) существует и в том случае, когда ограниченная функция U(x), не будучи сама монотонной, может быть представлена в виде суммы или разности двух ограниченных монотонных функций U U(x) = U1(x)-U2(x). т. е. является функцией с ограниченным изменением (см. Изменение функции). Если интегрирующая функция U(x) имеет ограниченную и интегрируемую по Риману производную U'(x), то интеграл Стилтьеса сводится к интегралу Римана по формуле 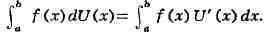 В частности, когда U(x) = х + С, интеграл Стилтьеса (9) превращается в обыкновенный интеграл Римана (6). Дальнейшие обобщения. Концепции И., созданные Стилтьесом и Лебегом, удалось впоследствии объединить и обобщить на интегрирование по любому (измеримому) множеству в пространстве любого числа измерений. Классич. кратные интегралы вполне охватываются этим подходом. Потребности таких дисциплин, как теория вероятностей и общая теория динамич. систем, привели к ещё более широкому понятию абстрактного интеграла Лебега, основанному на общих понятиях меры множества и измеримости функций. Пусть X - пространство, в к-ром выделена определённая система В его подмножеств, называемых "измеримыми", причём эта система обладает свойствами замкнутости по отношению к обычным теоретико-множественным операциям, выполняемым в конечном или счётном числе. Пусть ц - конечная мера, заданная на В. Для В-измеримой функции y = f(x),xXЄX, принимающей конечное или счётное число значений y..., уAf(x) по мере μ , обозначаемый . ∫xf(x)μ(dx) определяется как сумма ряда 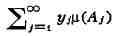 в предположении, что этот ряд абсолютно сходится. Для других f интегрируемость и И. определяются путём нек-рого естественного предельного перехода от указанных кусочно в предположении, что этот ряд абсолютно сходится. Для других f интегрируемость и И. определяются путём нек-рого естественного предельного перехода от указанных кусочно постоянных функций. Пусть А - измеримое множество и φA(x) = 1 для х, принадлежащих А, и для х, не принадлежащих А иφA(x)=0. Тогда интеграл от f(x) по множеству А определяют, полагая 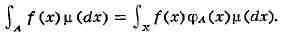 При фиксированных мю. и А И. в зависимости от f может рассматриваться как линейный функционал; при фиксированном f И., как функция множества А, есть счётно аддитивная функция. Следует отметить, что, несмотря на кажущуюся отвлечённость, это общее понятие И. в наибольшей степени подхо-дит для определения такого понятия, как матем. ожидание (в теории вероятностей), и даже для общей формулировки задачи проверки статистая, гипотез. И. по отношению к т. н. мере Вивера и различным её аналогам используют в статистич. физике (здесь в качестве X фигурирует пространство непрерывных на к.-л. отрезке функций). Упоминавшиеся до сих пор обобщения понятия И. были такими, что f и |f| оказывались интегрируемыми или неинтегрируемыми одновременно. Обобщения первоначального понятия И. в другом направлении относятся к функциям одного переменного, но зато дают много больше в исследовании интегрирования неогранич. функций. Ещё Коши " случае функции f(x), неограниченной в точке х = с, определил интеграл 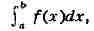 когда а<с<b, как предел выражения 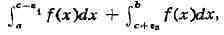 при 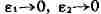 . Аналогично И. с бесконечными пределами . Аналогично И. с бесконечными пределами 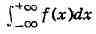 определяется как предел И. 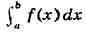 при 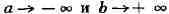 . Если при этом не требуется интегрируемости |f(x)|, т. е. f(x) интегрируема "не абсолютно", то это определение Коши не поглощается лебе-говским.
| |
| Просмотров: 3836 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта