Формула Шлетца - Математика - Математика - Каталог статей

Главная » Статьи » Математика » Математика

Формула Шлетца

§1. Пространство R(p₁,p₂).
А₁- аффинная прямая. Отнесем прямую А₁ к подвижному реперу
r = {a,`e}, где а и`e  соответственно точка и вектор.
Деривационные формулы репера r имеют вид:
d a= q`e , d`e= W`e  (1),
причем формы Пфаффа q и W подчиняются уравнениям структуры 1-мерного
аффинного пространства :
D q = qÙW , DW=WÙW=0.
Пусть e* - относительная длина вектора e* =`e + d`e + 1/2d²`e + 1/6d³`e +... по отношению к вектору `е. Тогда `e* =e*`e. Из (1) получаем :

e*=1+W+...

Таким образом, форма Пфаффа W является дифференциалом относительной

длины вектора `e* , близкого к `e , по отношению к `e.
Пусть R(p₁,p₂) – пространство всех пар (p₁,p₂) точек p₁,p₂ прямой А_1. Поместим
начало а репера r в середину Q отрезка р₁р₂, а конец
вектора `е – в точку р₁; при этом р₂ совместится с концом
вектора -`е.
Условия стационарности точек р₁ и р₂ в таком репере имеют
соответственно вид: W+q=0, -W+q=0.
Таким образом , в репере r структурными формами пространства R(р₁,р₂) являются формы Пфаффа : W+q , -W+q.
Очевидно, что dim R(p₁,p₂)=2. Заметим ,что в
репере r форма 2W является дифференциалом относительной длины отрезка 
р₁*р₂*, близкого к р₁р₂
,по отношению к р₁р₂.§ 2. Отображение f.
 А₂ – аффинная плоскость , отнесенная к подвижному реперу R
={p,`e_j}. Деривационные формулы репера R и уравнения
структуры плоскости А₂ имеют соответственно вид :dp=
W^je_j ; d`e_j= W_j^k; DW^j=W^k^W_k^j ; DW^j=W_j^y^W_y^k .
Рассмотрим локальное дифференцируемое отображение f плоскости А₂ 
в пространстве R(p₁,p₂):f:A₂®R(p₁,p₂).
Будем считать , что в каждой точке области определения отображения f выполняется
: rang f=2  (1)
Поместим начало Р репера R в точку f^-1(p₁
,p₂). Тогда дифференциальные уравнения отображения f 
запишутся в виде :
  Q+W=l_jW^j ; Q-W=m_jW^j  (2)
Из (1) вытекает , что существует локальное дифференцируемое отображение 
f^-1: R(p₁,p₂)®A₂ 
обратное к f.В указанных реперах дифференциальные уравнения отображения 
f^-1 имеют вид :
 W^j=l^j(Q+W)+m^j(Q-W)  (3)
Из (2) и (3) получаем :
 l^kl_j+m^km_j=d_j^k
 l^jl_j=1
 m^jm_j=1 (*)
 l^jm_j=0
 m^jl_j=0
Указанную пару {r;R} реперов пространств А₁ и А₂ будем называть репером нулевого порядка отображения f.
§3.Фундаментальные геометрические объекты отображения f.
Осуществим продолжение системы (2) дифференциального уравнений отображения f.
 D(λ_jW^j-W-Q)=0,
получаем :
  dλ_j=λ_kW_j^k+1\4(λ_jμ_k-λ_kμ_j)W^k+λ_jkW^k
 D(μ_jW^j+W-Q)=0
получаем :
  dμ_j=μ_kW_j^k+1\4(λ_jμ_k-λ_kμ_j)W^k+μ_jkW^k
Итак, продолженная система дифференциальных уравнений отображения f имеет вид :
  Q+W=λ_jW^j
 Q-W=μ_jW^j
 dλ_j=λ_kW_j^k+1\4(λ_jμ_k-λ_kμ_j)W^k+λ_jkW^k
 dμ_j=μ_kW_j^k+1\4(λ_jμ_k-λ_kμ_j)W^k+μ_jkW^j
Из этих уравнений вытекает, что система величин Г₁={λ_j
,μ_j} является геометрическим объектом. Он называется
фундаментальным геометрическим объектом первого порядка отображения f.
Осуществим второе продолжение системы (2) :
  dλ_k^W_j^k+λ_kdW_j^k+1\4(λjμ_k-λ_kμ_j)^W^k+1\4(λ_jμ_k-λ_kμ_j
)dW^k+dλ_jk^W^k+λ_jkdW^k=0.
получим:
 (dλ_jt-λ_ktW_j^k-λ_jkW_t^k+1\4(λ_kμ_jt
-μ_kλ_jk)W^k+1\16λ_t
μ_k(λ_j-μ_j)W^k)^W^t=0
 dμ_k^W_j^k+μ_kdW_j^k+1\4d(λ_jμ_k-λ_kμ_j
)^W^k+1\4(λ_jμ_k-λ_k
μ_j)dW^k+dμ_jk^W^k+μ_jkdW^k=0
получим:
 (dμ_jt-μ_ktW_j^k-μ_jtW_t^k+1\4(λ_kμ_jt
-μ_kλ_jt)W^k+1\16λ_t
μ_k(λ_j-μ_j)W^k)^W^t=0
обозначим:
 λ_j=dλ_j-λ_tW_j^t
 μ_j=dμ_j-μ_tW_j^t
 λ_jk=dλ_jk-λ_tkW_k^t-λ_jtW_k^t
 μ_jk=dμ_tkW_j^t-μ_jtW_k^t
Тогда дважды продолженная система дифференциальных уравнений отображения f
примет вид:
 Q+W=λ_jW^j
 Q-W=μ_jW^j
 dλ_j=λ_kW_j^k+1\4(λ_jμ_k-λ_kμ_j)W^k+λ_jkW^k
 dμ_j=μ_kW_j^k+1\4(λ_jμ_k-λ_kμ_j)W^k
+μ_jkW^k (4)
 λ_jk
=(1\4(μ_αλ_jk-λ_αμ_jk)+1\16λ_kμ_α(μ_j
-λ_j)+λ_jkα)W^α
 μ_jk
=(1\4(μ_αλ_jk-λ_αμ_jk)+1\16λ_kμ_α(μ_j
-λ_j)+μ_jkα)W^α
Из уравнений (4) вытекает, что система величин Г₂={λ_j,μ_j,λ_jk,μ_jk} образует
геометрический объект. Он называется фундаментальным геометрическим объектом
второго порядка отображения f. Дальнейшее продолжение системы (2) 
приведет к фундаментальному геометрическому объекту Г_Р 
порядка р :
 Г_Р={λ_j,μ_j,λ_j1j2,μ_j1j2,...,λ_j1j2...jp,μ_j1j2...jp}.
§ 4. Векторы и ковекторы первого порядка.
Из системы дифференциальных уравнений (5) вытекает, что система величин 
{λ_j},{μ_j} образует подобъекты
геометрического объекта Г₁. Будем называть их основными
ковекторами 1-го порядка. Основные ковекторы определяют для каждой точки P две
инвариантные прямые:
 λ_jX^j=1 ; μ_jX^j=1 (6)
не инцидентные точке Р. Из условия rang f=2 и уравнения (2) 
вытекает, что прямые (6) не параллельны. Условия (*) показывают,
что величины {λ^j,μ^j} являются
компонентами матрицы ,обратной к матрице, составленной из координат основных
ковекторов. Таким образом , величины {λ^j,μ^j
} охватываются объектом Г₁.
Из (*) получаем:
 dλ^j=-λ^kW_k^j-1\4(λ^j+μ^j)μ_tW^t-λ_kt
λ^kλ^tW^t-μ_ktW^t
^λ^kμ^j
 dμ^j=-μ^kW_k^j-λ_ktμ^kλ^jW^t-μ_kt
μ^kμ^jW^t+1\4λ_t(λ^j+μ^j)W^t
Таким образом , система величин и образуют геометрические объекты, охваченные
объектом Г₁. Будем называть их основными векторами 1-го
порядка.
Предположение 1.Конец вектора v₁=λ^je_j 
(вектора v₂=μ^je_j) лежит на прямой 
(6). Доказательство вытекает из формул (*),(2). Прямые, параллельные
прямым (6), инцидентные точке Р, определяются соответственно
уравнениями:
  λ_jX^j=0 , μ_jX^j = 0
(7).
Предположение 2. Основные векторы {λ^j} и {μ^j} параллельны прямым (6) соответственно. Доказательство
вытекает из формул (*) и (7). Взаимное расположение
рассмотренных векторов и прямых представлено на рисунке: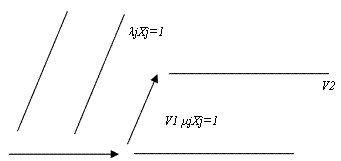


 
λ_jX^j=1
 
V₂
V₁ μ_jX^j=1
 
Система величин ρ_j=λ_j-μ_j 
образует ковектор: dρ_j=ρ_kW_j^k
+(μ_jk-λ_jk)W^k.
Определяемая им прямая ρ_jX^j=0 (8) проходит
через точку Р и точку пересечения прямых (6).
Пусть W-однородное подмногообразие в R(p₁,p₂) 
содержащее элементы (р₁,р₂) определяемое условием: 
(р₁^*,р₂^*)∈W↔p₁^*p₂^*=p₁p₂.
Теорема 1.Прямая (8) является касательной в точке Р к прообразу 
f^-1(W) многообразия W при отображении f.
Доказательство:
  ] (p₁^*,p₂^*)∈W и p₁^*=p₁+dp₁+1\2d²p₁+... ,
 p₂^*=p₂+dp₂+1\2d²p₂+... .
Тогда в репере Г: p₁^*p₂^*=e p₁p₂, где e=1+2W+... является относительной длиной
отрезка р₁^*р₂^* по отношению
к р₁р₂. Таким образом, (р₁^*
р₁^*)∈W↔W=0.
Из (2) получим: W=ρ₁W^j
Следовательно, (р₁^*р₂^*)∈W 
равносильно ρ_jW^j=0
(9)
Из (8) и (9) вытекает доказательство утверждения.
При фиксации элемента (р₁,р₂)∈R(p₁p₂) определяется функция h: (p₁^*p₂^*)∈h(p₁p₂)→e∈R,
так, что р₁^*р₂^*=е р₁
р₂
В дальнейшем эту функцию будем называть относительной длиной. Т.о., линия 
f^-1(W) является линией уровня функции h. Заметим, что 
(9) является дифференциальным уравнением линии f^-1(W).
 ]W₁,W₂- одномерные многообразия в R(p₁
p₂), содержащие элемент (р₁р₂) и
определяемые соответственно уравнениями:
 (p₁^*,p₂^*)єW₁↔p₂^*=p₂.
 (p₁^*,p₂^*)єW₂↔p₁^*=p₁.
Следующая теорема доказывается аналогично теореме 1.
Теорема 2. Прямая (7) является касательной в точке P к прообразу
многообразия W₂ (многообразия W₁) при
отображении f.
Дифференциальные уравнения линии f^-1(W₁) и f^-1(W₂) имеют соответственно вид:
 λ_jW^j=0 
 μ_jW^j=0.
Пусть W₀- одномерное подмногообразие в R(p₁p₂), содержащее (р₁р₂) и определяемое
условием: (p₁^*p₂^*)єW₀
↔Q*=Q ,где Q*– середина отрезка р₁^*р₂^*. Следующее утверждение доказывается аналогично теореме
1.
Предложение 3. Прямая (λ_j+μ_j)X^-j
=0 (10) является касательной в точке Р к прообразу f^-1
(W₀) многообразия W₀ при отображении f
. Дифференциальное уравнение линии f^-1(W₀) имеет
вид: (λ_j+μ_j)W^j=0.
Теорема 3.Прямые, касательные в точке Р к многообразиям f^-1
(W₁), f^-1(W₂), f^-1(W),
f^-1(W₀) составляют гармоническую четверку.
Доказательство вытекает из (7),(8),(10).
§5. Точечные отображения, индуцируемые отображением f.
Рассмотрим отображения:
 П₁: (р₁,р₂)∊R(p₁,p₂)→p₁∊A₁ (5.1)
 П₂: (р₁,р₂)∊R(p₁,p₂)→p₂∊A₁ (5.2)
Отображение f: A₂→R(p₁,p₂) порождает точечные отображения:
 φ₁=П₁∘f: A₂→A₁ (5.3)
 φ₂=П₂∘f: A₂→A₁ (5.4)
В репере нулевого порядка дифференциальные уравнения отображений φ₁ и φ₂ меют соответственно вид (2.5 а) 
и (2.5 б). Подобъекты Г_1,2={λ_j,λ_jk} и Г_2,2={μ_j,μ_jk} 
объекта Г₂ являются фундаментальными объектами второго
порядка отображений φ₁ и φ₂.
В работе <4> доказано, что разложение в ряд Тейлора отображений имеет
соответственно вид:
 x=1+λ_jX^j+1/2λ_jkX^jX^k+1/4λ_yρ_kX^jX^k+<3>, (5.5)
 y=-1+μ_jX^j+1/2μ_jkX^jX^k+1/4μ_yρ_kX^jX^k+<3>, (5.6)
Введем системы величин:
 Λ_jk=λ_jk+1/4(λ_jρ_k+λ_kρ_j),
 Μ_jk=μ_jk+1/4(μ_jρ_k+μ_kρ_j)
Тогда формулы (5.5) и (5.6) примут соответственно вид:
 x=1+λ_jX^j+1/2Λ_jkX^jX^k+<3> (5.7)
 y=-1+μ_jX^j+1/2Μ_jkX^jX^k+<3> (5.8)
В <4> доказано, что существует репер плоскости А₂, в котором выполняется:
 λ₁ λ₂ 1 0 
 = 
 μ₁ μ₂ 0 1 
Этот репер является каноническим.
Таким образом, в каноническом репере Якобиева матрица отображения f 
является единичной матрицей.
Формулы (5.7) и (5.8) в каноническом репере примут вид:
 x=1+X¹+1/2Λ_jkX^jX^k+<3> (5.9),
 y=-1+X²+1/2Μ_jkX^jX^k+<3> (5.10). 
§6. Инвариантная псевдориманова метрика.
Рассмотрим систему величин:
 G_jk=1/2(λ_jμ_k+λ_kμ_j)
Из (3.1) получим:
 dG_jk=1/2(dλ_jμ_k+λ_j
μ_k+dλ_kμ_j+λ_k
dμ_j)=1/2(μ_kλ_tW_j^t
+1/4λ_jμ_kμ_tW^t
-1\4μ_kμ_tλ_tW^t+μ_kλ_jtW^t+λ_jμ_tW_k^t+
+1/4λ_jλ_kμ_tW^t
-1/4μ_jλ_kμ_tW^t
-1/4μ_jλ_tμ_kW^t+μ_jλ_ktW^t+λ_kμ_tW_j^t+1/4λ_kλ_jμ_tW^t-1/4λ_kλ_tμ_jW^t+
+λ_kμ_jtW^t),
 dG_jk=1/2(μ_kλ_t+λ_k
μ_t)W_j^t+1/2(λ_jμ_t
+λ_tμ_j)W_k^t+G_jktW^t,
где G_jkt=1/2(μ_kλ_jt+λ_yμ_kt+μ_jλ_kt+λ_k
μ_jt-1/2μ_jμ_kλ^t
+1/2λ_jλ_kμ_t-1/4λ_j
μ_kλ_t+1/4λ_jμ_k
μ_t+1/4μ_jλ_kμ_t-
-1/4μ_jλ_kλ_t)  (6.3).
Таким образом, система величин {G_jk} образует двухвалентный
тензор. Он задает в А₂ инвариантную метрику G:
 dS²=G_jkW^jW^k (6.4)
Из (6.1) и (2.5) вытекает, что метрика (6.4) 
соответствует при отображении f метрике dS²=θ²
-W² (6.5) в R(p₁,p₂).
Из (6.5) вытекает, что метрика G является псевдоримановой метрикой.
Асимптотические направления определяются уравнением G_jkW^jW^k=0 или
 λ_jW^jμ_kW^k=0 (6.6)
 Предложение: Основные векторы V₁ и V₂ 
определяют асимптотические направления метрики G.
Б. А. Розенфельдом изучалась инвариантная метрика в пространстве нуль-пар. На
проективной прямой нуль-парой является пара точек. Для двух пар точек (x,U) 
и (y,U^’) расстояние между ними определяется как двойное
отношение W=(xy,UU^’)
 Теорема: Метрика dS²=θ²-W² совпадает с метрикой Розенфельда .
Доказательство: В репере r имеем для координат точек p₁,p₂,p₁+dp₁,p₂+dp₂
Соответственно: 1,-1,1+θ+W,-1+θ-W.
Подставляя их в формулу (4.2) на стр. 344 (§7), получаем
 dS²=θ²-W²
 Следствие: Метрика G сохраняется при расширении фундаментальной
группы ее проективных преобразований.
В работе <3> был построен охват объекта
 Г^l_jk=1/2G^tl(G_tkj+G_jtk-G_jkt)
 
псевдоримановой связности G фундаментальным объектом Г₂
={λ_j,μ_j,λ_jk,μ_jk
}.
Он определяется формулой: Г^l_jk=λ^j
Λ_jk+μ^lΜ_jk-λ^l
λ_tλ_k+μ^lμ_tμ_k.
§7. Инвариантная риманова метрика.
Рассмотрим систему величин:
 g_jk=λ_jλ_k+μ_jμ_k (7.1)
Из (3.1) получаем:
 dg_jk=dλ_jλ_k+dλ_k
λ_j+dμ_jμ_k+dμ_k
μ_j=λ_kλ_tW_j^t
+1/4λ_kλ_jμ_tW^t
-1/4λ_jλ_tμ_jW^t+λ_kλ_jtW^t+λ_jλ_tW_k^t+
+1/4λ_jλ_kμ_tW^t
-1/4λ_jλ_tμ_kW^t+λ_jλ_ktW^t+μ_kμ_tW_j^t+1/4μ_kλ_jμ_tW^t-1/4μ_kλ_tμ_jW^t
+μ_kμ_jtW^t+
+μ_jμ_tW_k^t+1/4μ_j
λ_kμ_tW^t-1/4μ_jλ_tμ_kW^t+μ_jμ_ktW^t.
 dg_jk=(λ_kλ_t+μ_k
μ_t)W_j^t+(λ_jλ_t
+μ_jμ_t)W_k^t+g_jktW^t, (7.2)
где g_jkt=1/2λ_jλ_kμ_t
-1/2μ_jμ_kλ_t-1/4λ_k
λ_tμ_j-1/4λ_jλ_t
μ_k+1/4λ_jμ_kμ_t
+1/4μ_jλ_kμ_t+λ_k
λ_jt+λ_jλ_kt+
 +μ_kμ_jt+μ_jμ_kt (7.3)
Таким образом, система величин {g_jk} образует двухвалентный
тензор. Он задает в А₂ инвариантную метрику g:
 dS²=g_jkW^jW^k (6^’.4)
Из (7.1) и (2.5) вытекает, что метрика (6^’.4) 
соответствует при отображении f метрике:
 dS²=2(θ²+W²) (6^’.5)
в R(p₁,p₂)
Из (6^’.5) вытекает, что метрика g является римановой метрикой.
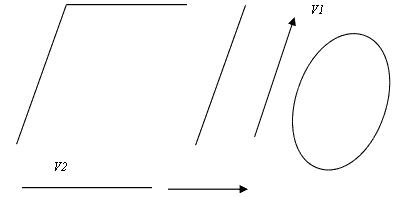
Единичная окружность, построенная для точки Р определяется уравнением:
 GjkXjXk=1 (6^’.6)
или (λ_jX^j)²+(μ_jX^j)²=1 (6^’.7)
Из (6^’.7) вытекает:
 Предложение 7.1: Единичная окружность метрики g с центром в точке 
Р является эллипсом, касающимся в концах основных векторов прямых,
параллельных этим векторам.
Заметим, что сформулированное здесь свойство единичной окружности полностью
определяет эту окружность, а следовательно и метрику g.
 
 
.
Пусть g^jk=λ^jλ^k+μ^jμ^k (6.8)
В силу (2.7) имеем:
 g^jtg_tk=(λ^jλ^t+μ^jμ^t)(λ_tλ_k+μ_t
μ_k)=λ^jλ^k+μ^j
μ^k=δ_k^j (6^’.9)
Таким образом, тензор g^jk является тензором взаимных к g_jk. Как известно, метрика ставит в соответствие каждому векторному
полю поле ковектора и наоборот.
 Предложение 7.2: Поле основного вектора {λ^j} 
(вектора {μ^j}) соответствует в метрике g полю
основного ковектора {λ_j} (ковектора {μ_j
}).
Доказательство: Основные векторы ортогональны друг другу и имеют единичную длину
в метрике g.
Доказательство:
 λ^jλ^kg_jk=λ^jλ^kλ_jλ_k+λ^jλ^kμ_jμ_k=1,
 μ^jμ_kg_jk=μ^jμ^kλ_jλ_k+μ^jμ^kμ_jμ_k=1,
 λ^jμ^kg_jk=λ^jμ^kλ_jλ_k+λ^jμ^kμ_jμ^k=0.
Таким образом, f задает на А₂ структуру риманова пространства (A₂,g_f).
В работе <2> был построен охват объекта
 γ_jk^l=1/2g^tl(g_tkj+g_jtk-g_jkt)
римановой связности γ фундаментальным объектом
 Г₂={λ_j,μ_j,Λ_jk,Μ_jk}
Он определяется формулой:
 γ_jk^l=λ^lΛ_jk+μ^lM_jk+G_jk(λ^l-μ^l
)+1/2(λ^l+μ^l)(μ_jμ_k
-λ_jλ_k),
где G_jk=1/2(λ_jμ_k+λ_kμ_j).