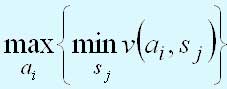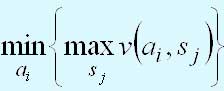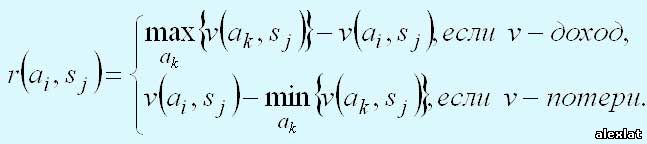$AlexLat$

Отличие между принятием решений в условиях риска и неопределенности состоит в том, что в условиях неопределенности вероятностное распределение, соответствующее состояниям sj, j = 1, 2, ..., n, либо неизвестно, либо не может быть определено. Этот недостаток информации обусловил развитие следующих критериев для анализа ситуации, связанной с принятием решений.

  Критерий Лапласа

  Минимаксный критерий

  Критерий Сэвиджа

  Критерий Гурвица

    Эти критерии отличаются по степени консерватизма, который проявляет индивидуум, принимающий решение, перед лицом неопределенности.

Критерий Лапласа

    Критерий Лапласа опирается на принцип недостаточного основания, который гласит, что, поскольку распределение вероятностей состояний P(si) неизвестно, нет причин считать их различными. Следовательно, используется оптимистическое предположение, что вероятности всех состояний природы равны между собой, т.е. P{s1} = P{s2} = ... = P{sn} = 1/n. Если при этом v(аi, sj) представляет получаемую прибыль, то наилучшим решением является то, которое обеспечивает

    Если величина v(аi, sj) представляет расходы лица, принимающего решение, то оператор "max" заменяется на "min".

Минимаксный критерий

    Максиминный (минимаксный) критерий основан на консервативном осторожном поведении лица, принимающего решение, и сводится к выбору наилучшей альтернативы из наихудших. Если величина v(аi, sj) представляет получаемую прибыль, то в соответствии с максиминным критерием в качестве оптимального выбирается решение, обеспечивающее

     Если величина v(аi, sj) представляет потери, используется минимаксный критерий, который определяется следующим соотношением.

Критерий Сэвиджа

    Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем замены матрицы платежей (выигрышей или проигрышей) v(аi, sj) матрицей потерь r(аi, sj), которая определяется следующим образом.

   Чтобы показать, как критерий Сэвиджа "смягчает" минимаксный (максиминный) критерий, рассмотрим следующую матрицу платежей v(аi, sj):

Таблица 1. Матрица платежей

Применение минимаксного критерия приводит к тому, что решение а₂ с фиксированными потерями в 10000 долл. является предпочтительным. Однако можно выбрать и а₁ так как в этом случае существует возможность потерять лишь 90 долл., если реализуется состояние s₂, при потенциальном выигрыше 11 000 долл. Посмотрим, какой результат получится, если в минимаксном критерии вместо матрицы платежей v(аi, sj) использовать матрицу потерь r(аi, sj).

Таблица 2. Матрица потерь

    Как видим, минимаксный критерий, применяемый к матрице потерь, приводит к выбору решения ах в качестве предпочтительного.

Критерий Гурвица

    Рассмотрим теперь критерий Гурвица. Этот критерий охватывает ряд различных подходов к принятию решений — от наиболее оптимистичного до наиболее пессимистичного (консервативного). Пусть 0 <= а <= 1 и величины

v(аi, sj) представляют доходы. Тогда решению, выбранному по критерию Гурвица, соответствует

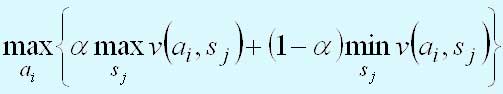
    Параметр а - показатель оптимизма.

Если a = 0, критерий Гурвица становится консервативным, так как его применение эквивалентно применению обычного минимаксного критерия.

Если а = 1, критерий Гурвица становится слишком оптимистичным, ибо рассчитывает на наилучшие из наилучших условий.

    Можно конкретизировать степень оптимизма (или пессимизма) надлежащим выбором величины a интервала [0,1]. При отсутствии ярко выраженной склонности к оптимизму или пессимизму выбор а = 0,5 представляется наиболее разумным.

    Если величины v(аi, sj) представляют потери, то критерий принимает следующий вид:

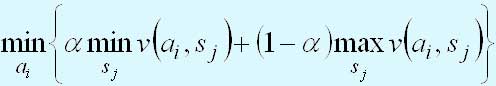
     На следующем шаге мы рассмотрим применение критериев принятия решений в условиях неопределенности.