| Главная » Статьи » Математика » Математика |
Критерии согласия: критерий χ² ПирсонаКритерий χ² (K.Pearson, 1900) основывается на группированных данных. Область значений предполагаемого распределения делят на некоторое число интервалов. После чего строят функцию отклонения ρ по разностям теоретических вероятностей попадания в интервалы группировки и эмпирических частот. Имеется выборка χ =( χ1,...,χn) из распределения F . Проверяется простая гипотеза против сложной альтернативы H1=(F = F1). Пусть,A1,..., Ak , , — интервалы группировки в области значений случайной величины с распределением . Обозначим для j = l,...,k через vj число элементов выборки, попавших в интервал Aj
и через ρ > 0 — теоретическую вероятность PH (χi ε Aj) попадания в интервал Aj случайной величины с распределением Пусть
Замечание 18. Свойство K1(б) выполнено далеко не для всех альтернатив. Если распределение выборки F2 ≠ F1 имеет такие же, как у F1 , вероятности ρj попадания в каждый из интервалов Aj , то по данной функции эти распределения различить невозможно. Поэтому на самом деле критерий, который мыпостроим по функции ρ из(23),решает совсем иную задачу. А именно, пусть задан набор вероятностей ρ1,... ρk такой, что ρ1+...+ρk = 1. Критерий χ² предназначен для проверки сложной гипотезы
против сложной альтернативы
Покажем, что ρ⒳удовлетворяет условию K1(a). Теорема Пирсона. Если верна гипотеза H’1,
где, напомним, Hk-1 есть χ² - распределение с k-1 степенью свободы. Стоит остановиться и задать себе вопрос. Величина ρ есть сумма k слагаемых. Слагаемые, если вы не забыли ЦПТ или теорему Муавра — Лапласа, имеют распределения, близкие к квадратам каких-то нормальных. Куда потерялась одна степень свободы? Причина кроется, конечно, в зависимости слагаемых: vk = n - v1-...-vk-1. Докажем теорему Пирсона при k = 2 . В этом случае v2 = n - v1, ρ 2 = 1, . Посмотрим на ρ и
Но величина v1 есть сумма n независимых случайных величин
где ξ имеет стандартное нормальное распределение. Поэтому
Величина ξ² имеет χ² -распределение H1 с одной степенью свободы. Q.D.E. Функция ρ⒳удовлетворяет условиюK1(б) Действительно, Упражнение. Вспомнить закон больших чисел и доказать, что если H’1 неверна, то найдется jε{1,...,k}. такое, что 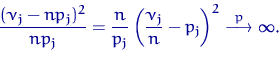 Осталось построить критерий в соответствии с K2.
Замечание 19. На самом деле критерий χ² применяют и для решения первоначальной Замечание 20.
Сходимость по распределению ρ⒳→ Hk-1 обеспечивается ЦПТ, поэтому разница допредельной и предельной вероятностей
где b — некоторая постоянная. Маленькие значения nρj в знаменателе | |||
| Просмотров: 1621 | | |||
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
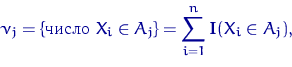
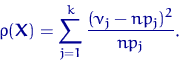

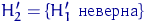 , т.е.
, т.е. 
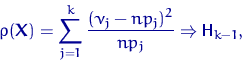
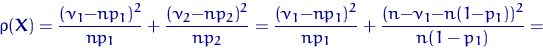
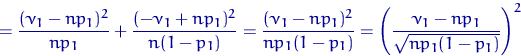 .
.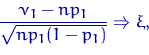
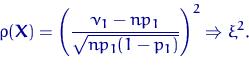
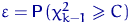 и
и 
