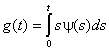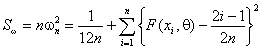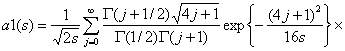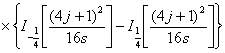| Главная » Статьи » Математика » Математика |
Критерий w²Крамера-Мизеса-Смирнова при простой гипотезеПорядок проверки простой гипотезы о согласииПростая проверяемая гипотеза имеет вид H0: F(x)=F(x,q), где F(x,q) – функция распределения вероятностей, с которой проверяется согласие наблюдаемой выборки, а q – известное значение параметра (скалярного или векторного). В случае простых гипотез предельные распределения статистик критерия согласия w 2не зависят от вида наблюдаемого закона распределения F(x,q) и, в частности, от его параметров. Говорят, что эти критерии являются "свободными от распределения”. Это достоинство предопределяет широкое использование данных критериев в приложениях.При проверке согласия опытного распределения с теоретическим распределением случайной величины X:1. Формулируют проверяемую гипотезу, выбирая теоретическое распределение случайной величины, согласие которого с опытным распределением этой величины следует проверить.2. Из совокупности отбирают случайную выборку объема n. Полученные результаты наблюдений располагают в порядке их возрастания, так что в распоряжении имеют упорядоченную выборку значенийx1 ≤ x2 ≤ … ≤ xn.3. В соответствии с выбранным критерием проверки вычисляют значение статистики S* критерия w² Мизеса.4. В соответствии с выбранным критерием проверки вычисляют значение | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Рост, см |
F(x;Θ) |
S* |
|
114 |
0,09375 |
1,596169 |
|
120 |
0,098684 |
|
|
125 |
0,102796 |
|
|
133 |
0,109375 |
|
|
139 |
0,114309 |
|
|
139 |
0,114309 |
|
|
145 |
0,119243 |
|
|
150 |
0,123355 |
|
|
151 |
0,124178 |
2. a1(S*)≈ 0,999 (из таблицы 1)
3. На уровне значимости α = 0,05 в таблице 2 находим a1(S)=0,4614.
4. Подтверждение гипотезы находим по формуле: P{S>S*}=1-a1(S*)>a
P{S<1,59}=1-0,999>a => 0,01<0,5.
Гипотезу Но опровергаем, выборка не находится в согласии с теоретическим распределением.
Пример 2.
Гипотеза Н0: Количество рыбы в сезон на Аляске, за последние 5 лет, теоретически согласовано.
1. Имеются данные о количестве рыбы (в млн кг), обрабатываемой в рыбный сезон на заводе «Seward Fisheries» на Аляске:
1,5; 0,8; 1; 0,6; 1,2.
|
Вес, млн кг |
F(x;Θ) |
Сумма |
S* |
|
0,6 |
0,117647 |
0,000311 |
0,71288 |
|
0,8 |
0,156863 |
0,020488 |
|
|
1 |
0,196078 |
0,092368 |
|
|
1,2 |
0,235294 |
0,215952 |
|
|
1,5 |
0,294118 |
0,367093 |
2. a1(S*)= 0, 99036 (из таблицы 1)
3. На уровне значимости α = 0,01 a1(S)= 0,7434.
4. Подтверждение гипотезы находим по формуле: P{S>S*}=1-a1(S*)>a
P{S<0,71288}=1-0, 99036 <a => 0,00964<0,01.
Гипотезу Но опровергаем, количество рыбы на Аляске теоретически не согласовано.
Пример 3.
Гипотеза Н0: Средний балл студента Иванова И.И. за последние 5 сессий согласован с теоретическим распределением.
1. Средние баллы за каждую из 5 последних сессий такие:
4; 4,2; 4; 4,3; 4.
|
Оценка |
F(x;Θ) |
Сумма |
S* |
|
4 |
0,195122 |
0,012497 |
0,594398 |
|
4,2 |
0,204878 |
0,002036 |
|
|
4 |
0,195122 |
0,049082 |
|
|
4,3 |
0,209756 |
0,13956 |
|
|
4 |
0,195122 |
0,30789 |
2. a1(S*)= 0, 98314 (из таблицы 1)
3. На уровне значимости α =0,1, пользуясь таблицей 2, находим a1(S)= 0,3473.
4. Подтверждение гипотезы находим по формуле: P{S>S*}=1-a1(S*)>a
P{S<0,594398}=1-0, 98314 <a => 0,01686<0,1.
Гипотезу Но, оценки студента теоретически не согласованы.
Таблица 1
|
Функция распределения статистики w 2 Мизеса a1(S) при проверке простой гипотезы |
||||||||||
|
S |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,0 |
0,00000 |
00001 |
00300 |
02568 |
06685 |
12372 |
18602 |
24844 |
30815 |
36386 |
|
0,1 |
0,41513 |
46196 |
50457 |
54329 |
57846 |
61042 |
63951 |
66600 |
69019 |
71229 |
|
0,2 |
0,73253 |
75109 |
76814 |
78383 |
79829 |
81163 |
82396 |
83536 |
84593 |
85573 |
|
0,3 |
0,86483 |
87329 |
88115 |
88848 |
89531 |
90167 |
90762 |
91317 |
91836 |
92321 |
|
0,4 |
0,92775 |
93201 |
93599 |
93972 |
94323 |
94651 |
94960 |
95249 |
95521 |
95777 |
|
0,5 |
0,96017 |
96242 |
96455 |
96655 |
96843 |
97020 |
97186 |
97343 |
97491 |
97630 |
|
0,6 |
0,97762 |
97886 |
98002 |
98112 |
98216 |
98314 |
98406 |
98493 |
98575 |
98653 |
|
0,7 |
0,98726 |
98795 |
98861 |
98922 |
98981 |
99036 |
99088 |
99137 |
99183 |
99227 |
|
0,8 |
0,99268 |
99308 |
99345 |
99380 |
99413 |
99444 |
99474 |
99502 |
99528 |
99553 |
|
0,9 |
0,99577 |
99599 |
99621 |
99641 |
99660 |
99678 |
99695 |
99711 |
99726 |
99740 |
|
1,0 |
0,99754 |
99764 |
99776 |
99787 |
99799 |
99812 |
99820 |
99828 |
99837 |
99847 |
|
1,1 |
0,99856 |
99862 |
99869 |
99876 |
99883 |
99890 |
99895 |
99900 |
99905 |
99910 |
|
1,2 |
0,99916 |
99919 |
99923 |
99927 |
99931 |
99935 |
99938 |
99941 |
99944 |
99947 |
|
1,3 |
0,99950 |
99953 |
99955 |
99957 |
99959 |
99962 |
99964 |
99965 |
99967 |
99969 |
|
1,4 |
0,99971 |
99972 |
99973 |
99975 |
99976 |
99978 |
9997 | |||
Таблица 2
|
Процентные точки распределения статистики w 2 Мизеса при проверке простой гипотезы |
|||||
|
Функция распределения |
Верхние процентные точки |
||||
|
0,15 |
0,1 |
0,05 |
0,025 |
0,01 |
|
|
a1(S) |
0,2841 |
0,3473 |
0,4614 |
0,5806 |
0,7434 |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
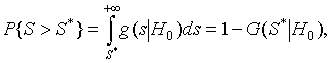
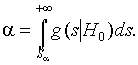
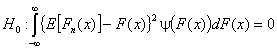
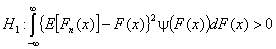
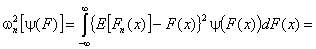
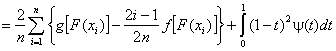 ,
, 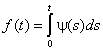 ,
,