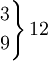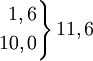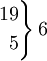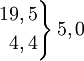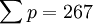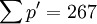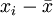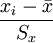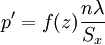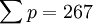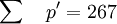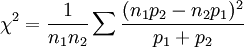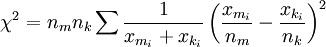| Главная » Статьи » Математика » Математика |
Словарь-справочник по психодиагностикеКритерий χ² (критерий согласия Пирсона) — характеристика распределения, используемая для проверки статистических гипотез. Под статистическим критерием подразумевается правило, обеспечивающее с определенной вероятностью принятие истинной или отклонение ложной гипотезы. В качестве критериев в математической статистике применяют определенные случайные величины, являющиеся функциями изучаемых случайных величин и чисел степеней свободы. Одним из наиболее часто применяемых является К. χ² представляющий собой сумму квадратов отклонений эмпирических частот (р) от теоретических или ожидаемых (P’), отнесенную к теоретическим частотам: При полном совпадении эмпирических и ожидаемых частот S(p - p’) = 0 . При несовпадении производится сравнение эмпирической величины χ² с его критическим значением, определенным по таблицам . Нулевая гипотеза, которая предполагает, что расхождение между эмпирическими частотами и математическим ожиданием носит случайный характер и между вычисленными и эмпирическими частотами разницы нет, опровергается, если < math > χ² ≥ χ2kp</math> для принятого уровня значимости (α) и числа степеней свободы (df). В качестве примера проанализируем с помощью К. χ² распределение частот выбора ответа на закрытый пункт теста. Предлагаемые варианты неправильных ответов должны быть примерно равновероятны. При обследовании 100 человек, отвечающих на проверяемый пункт неверно, результаты распределились следующим образом (табл. 1). Таблица 1
В качестве другого примера рассмотрим проверку нормальности распределения тестовых оценок (см. Оценка типа распределения). Исходные данные приведены в табл. 2, 3. Число степеней свободы определяется в данном случае исходя из свойств нормального распределения df = k − 3 (ограничения свободы вариации Как видно из данного примера, для проверки гипотезы о законе распределения необходимо сопоставить эмпирические и расчетные теоретические частоты. Последние рассчитываются на основании эмпирических данных по формулам, описывающим тот или иной закон распределения вероятностей. Так, для проверки нормальности распределения теоретические частоты рассчитываются по формуле: где P’ — теоретически вычисленные или ожидаемые частоты эмпирического ряда, f(z) — значение функции нормированного отклонения, n — общее число наблюдений, λ — величина классового интервала или промежуток между соседними классами эмпирического ряда, Sx — среднее квадратичное отклонение эмпирического ряда. Для приведенного выше примера расчет сводится к нормированию эмпирического ряда, т. е. отнесению отклонений xi от средней x к величине Sx. Затем по табл. 1 (Основных статистических таблиц) определяются значения ординаты ноомальной кривой f(z) для каждого Таблица 2
Таблица 3
К. χ2 можно использовать для сравнения эмпирических рядов с частотами, распределенными по одним и тем же классам. В этом случае применяется формула: где n1,n2 — объемы сравниваемых выборок, p1,p2 — частоты первого и второго рядов. Нулевая гипотеза сводится к тому, что сравниваемые выборки взяты из одной и той же совокупности генеральной и, следовательно, несовпадение между частотами p1,p2 носит случайный характер. К. n1,n2 обычно используется для проверки гипотез о соответствии (согласии) эмпирического распределения теоретическому (см. приведенные выше примеры), при проверке гипотез о статистической независимости признаков (при x² > x²kp предложение об отсутствии связи между признаками отвергается). Теснота связи может быть рассчитана с помощью коэффициента сопряженности Пирсона (см. Корреляция качественных признаков), при подтверждении гипотезы об однородности распределения признаков в разных совокупностях (в этом случае нулевая гипотеза формулируется как предположение о сходстве распределения признака в двух генеральных совокупностях, из которых взяты независимые выборки объемами nm,nk): Преимуществами К. χ2 являются применимость его для различных распределений дискретных и непрерывных признаков, необязательность предварительных сведений о законе распределения изучаемой переменной. При использовании К. χ2 следует учитывать такие ограничения:
Если это требование не выполняется, необходимо увеличить объем выборки или объединить интервалы группировки, суммируя их частоты (см. выше пример сравнения эмпирического и нормального распределения). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 2623 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |

 )
)
 )
)
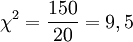
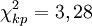 . Полученное значение
. Полученное значение 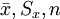 ). В результате объединения частот в крайних классах (см. ниже) число классов сократилось с 9 до 7, тогда
). В результате объединения частот в крайних классах (см. ниже) число классов сократилось с 9 до 7, тогда 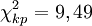
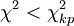 , Xследовательно, распределение тестовых оценок идет по нормальному
закону, расхождения между эмпирическим и нормальным распределением
случайны и несущественны.
, Xследовательно, распределение тестовых оценок идет по нормальному
закону, расхождения между эмпирическим и нормальным распределением
случайны и несущественны.
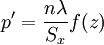
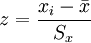 . Значения
. Значения 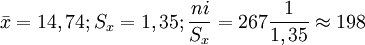 . Пример расчета приведен в таблице 3.
. Пример расчета приведен в таблице 3.
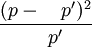
 )
)