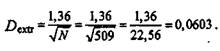| Главная » Статьи » Математика » Математика |
Метод монте-карло и проверка статистических гипотезСтатистические испытания по методу Монте-Карло представляют собой простейшее имитационное моделирование при полном отсутствии каких-либо правил поведения. Получение выборок по методу Монте-Карло - основной принцип компьютерного моделирования систем, содержащих стохастические или вероятностные элементы. Зарождение метода связано с работой фон Неймана и Улана в конце 1940-х гг., когда они ввелндая^еш^швание. .Мойте-Карло и применили его к решению некоторых задач экранирования ядерных излучений. Этот математический метод был известен и ранее, но свое второе рождение нашел в Лос-Аламосе в закрытых работах по ядерной технике, которые велись под кодовым обозначением Монте-Карло. Применение метода оказалось настолько успешным, что он получил распространение и в других областях, в частности в экономике. Поэтому многим специалистам термин метод Монте-Карло иногда представляется синонимом термина имитационное моделирование, что в общем случае неверно. Имитационное моделирование - это более широкое понятие, и метод Монте-Карло является важным, но далеко не единственным методическим компонентом имитационного моделирования. Согласно методу Монте-Карло проектировщик может моделировать работу тысячи сложных систем, управляющих тысячами разновидностей подобных процессов, и исследовать поведение всей группы, обрабатывая статистические данные. Другой способ применения этого метода заключается в том, чтобы моделировать поведение системы управления на очень большом промежутке модельного времени (несколько лет), причем астрономическое время выполнения моделирующей программы на компьютере может составить доли секунды. Рассмотрим метод Монте-Карло подробнее. В различных задачах, встречающихся при создании сложных систем, могут использоваться величины, значения которых определяются случайным образом. Примерами таких величин являются: случайные моменты времени, в которые поступают заказы на фирму; загрузка производственных участков или служб объекта экономики; внешние воздействия (требования или изменения законов, платежи по штрафам и др.); оплата банковских кредитов; поступление средств от заказчиков; ошибки измерений. В качестве соответствующих им переменных могут использоваться число, совокупность чисел, вектор или функция. Одной из разновидностей метода Монте-Карло при численном решении задач,-включающих случайные переменные, является метод статистических испытаний, который заключается в моделировании случайных событий. Метод Монте-Карло основан на статистических испытаниях и по природе своей является экстремальным, может применяться для решения полностью детерминированных задач, таких, как обращение матриц, решение дифференциальных уравнений в частных производных, отыскание экстремумов и численное интегрирование. При вычислениях методом Монте-Карло статистические результаты получаются путем повторяющихся испытаний. Вероятность того, что эти результаты отличаются от истинных не более чем на заданную величину, есть функция количества испытаний. В основе вычислений по методу Монте-Карло лежит случайный выбор чисел из заданного вероятностного распределения. При практических вычислениях эти числа берут из таблиц или получают путем некоторых операций, результатами которых являются псевдослучайные числа с теми же свойствами, что и числа, получаемые путем случайной выборки. Имеется большое число вычислительных алгоритмов, которые позволяют получить длинные последовательности псевдослучайных чисел. Один из наиболее простых и эффективных вычислительных методов получения последовательности равномерно распределенных случайных чисел г, с помощью, например, калькулятора или любого другого устройства, работающего в десятичной системе счисления, включает только одну операцию умножения.
Применение метода Монте-Карло может дать существенный эффект при моделировании развития процессов, натурное наблюдение которых нежелательно или невозможно, а другие математические методы применительно к этим процессам либо не разработаны, либо неприемлемы из-за многочисленных оговорок и допущений, которые могут привести к серьезным погрешностям или неправильным выводам. В связи с этим необходимо не только наблюдать развитие процесса в нежелательных направлениях, но и оценивать гипотезы о параметрах нежелательных ситуаций, к которым приведет такое развитие, в том числе и параметрах рисков. Существуют различные методы проверки статистических гипотез. Наиболее широко используются на практике критерии: согласия %2 (хи-квадрат); Крамера-фон Мизеса; Колмогорова-Смирнова. Критерий %2 предпочтителен, если объемы выборок N, в отношении которых проводится анализ, велики. Это мощное средство, если N>0 значений. Однако при анализе экономических ситуаций иногда бывает довольно трудно (или невозможно) найти 100 одинаковых процессов, развивающихся с различными исходными данными. Сложность заключается не только в том, что не бывает одинаковых объектов экономики: даже если такие объекты имеются, то к исходным данным относятся не только исходные вероятностные данные и особенности структуры объекта, но и сценарий развития процессов в этом объекте и в тех объектах внешней среды, с которыми он взаимодействует (процессы рынка, указы правительства, принятие новых законов, требования налоговых органов, платежи в бюджеты различных уровней). При относительно малых объемах выборок этот критерии вообще неприменим. Критерий Крамера-фон Мизеса дает хорошие результаты при малых объемах выборок (при N < 10). Однако следует отметить два обстоятельства: при N< 10, каким бы методом ни пользоваться, вопрос о доверительной вероятности при проверке статистической гипотезы решается плохо (эта вероятность мала при значительных размерах доверительных интервалов); метод Монте-Карло используется как раз для того, чтобы недостающие данные собрать с помощью специального вычислительного статистического инструментария и компьютера. Поэтому будем полагать, что реальные объемы выборок, которые можно получить, находятся в пределах 10 ЈN< 100. Как указывают многие исследователи, для указанных пределов хорошие результаты дает критерий Колмогорова-Смирнова. Он применяется в тех случаях, когда проверяемое распределение непрерывно и известны среднее значение и дисперсия проверяемой совокупности. Рассмотрим подробнее методику использования этого критерия на конкретном примере. Пример 1.1. Предположим, что нужно проверить данные, полученные (или наблюдаемые) при использовании метода Монте-Карло и приведенные в табл. 1.1, на их соответствие распределению Пуассона . Эти данные имеют следующий смысл. На отрезке времени наблюдаем случайные события, число которых равно х. Если это распределение Пуассона, то вероятность Р{х = п} того, что х = п, где п - заданное число, равна
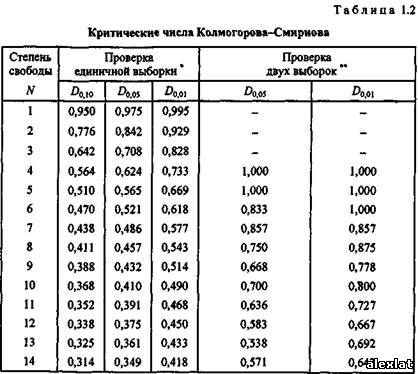
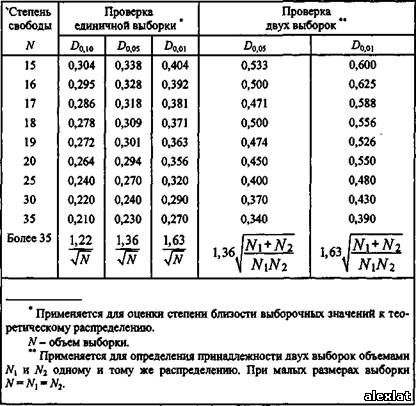
содержит наблюдаемую частоту появления п событий, а столбец 2 -наблюдаемую вероятность появления п событий. В столбце 3 представлены рассчитанные по формуле значения вероятности появления п событий. Прежде всего нужно получить два интегральных распределения (фактически приближения функций распределения). Сначала сделаем это для наблюдаемых данных: с помощью столбца 2 получим столбец 4. Затем - для теоретических данных: с помощью столбца 3 получим столбец 5. После этих вычислений найдем абсолютные разности для всех групп значений случайной величины и с помощью столбцов 4 и 5 получим столбец 6. В последнем столбце наибольшая абсолютная разность 0,048 получается в группе, соответствующей нулевому числу событий. Далее необходимо найти так называемое критическое значение Dexti для проверки принятой гипотезы. Таблица критических чисел многократно переиздавалась. Критические числа в виде, удобном для выполняемой проверки, приведены в табл. 1.2. Абсолютную разность 0,048 необходимо сравнить с критическим значением, найденным по табл. 1.2.
При л=509 и значении индекса критического числа Da a = 0,05 получается кштическое значение
Поскольку наибольшая разность 0,048 < /)& то не отказываемся от гипотезы о том, что экспериментальное распределение -пуассйновское. Проверка статистических гипотез о соответствии событий явлению и явлений поведению дает математический инструмент для оценки рискованного поведения исследуемого процесса. | |
| Просмотров: 1952 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
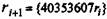 mod 1, где mod 1 означает операцию извлечения
mod 1, где mod 1 означает операцию извлечения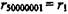 Последовательность rt получается равномерно распределенной на интервале
(0, 1). Ниже будут рассмотрены более точные способы получения таких
чисел со значительно большими периодами, а также пояснения, как в
реальных моделях такие числа становятся практически случайными.
Последовательность rt получается равномерно распределенной на интервале
(0, 1). Ниже будут рассмотрены более точные способы получения таких
чисел со значительно большими периодами, а также пояснения, как в
реальных моделях такие числа становятся практически случайными.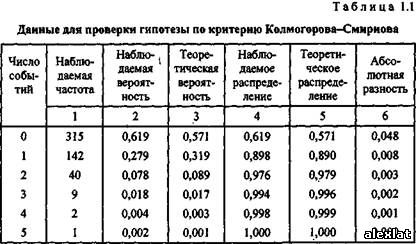
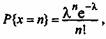
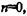 ... , 5, столбец 1
... , 5, столбец 1