| Главная » Статьи » Математика » Математика |
Полимино
Полимино. (Polyominoes) 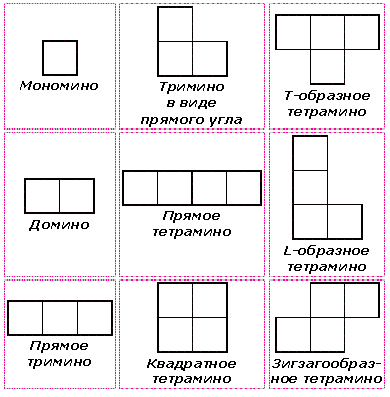 Рис. 64. Термин «полимино» ввел в употребление известный математик Соломон В. Голомб. В своей статье «Шахматные доски и полимино», написанной им еще в бытность его аспирантом Гарварда, Голомб определил полимино как «односвязную» фигуру, составленную из квадратов. Односвязность фигуры означает, что каждый входящий в нее квадрат имеет по крайней мере одну сторону, общую с другим входящим в нее же квадратом. Шахматист, добавляет Голомб, сказал бы, что квадраты составлены «ходом ладьи», потому что ладья могла бы обойти все квадраты полимино за конечное число ходов. На рис. 64 показаны мономино и все возможные фигуры полимино из двух, трех и четырех квадратов. 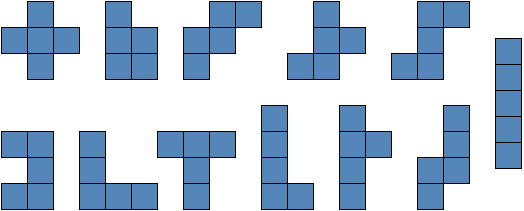 Рис. 65. Существует только один тип домино, два типа тримино и пять типов тетрамино. У пентамино число различных фигур возрастает сразу до двенадцати. Все они показаны на рис. 65. Асимметричные фигуры, переходящие друг в друга при переворачивании, считаются одной и той же фигурой. Во всех развлечениях с полимино, о которых пойдет речь в этой главе, наряду с любой асимметричной фигурой можно использовать и ее зеркальное отражение. Число различных полимино данного порядка, разумеется, зависит от того, из скольких квадратов составлены фигуры (то есть от порядка), но пока еще никому не удалось найти формулу, выражающую эту связь. Чтобы найти число различных «костей» n-мино высшего порядка, приходится пускаться в утомительные вычисления, отнимающие уйму времени.  Рис. 66. Существует 35 различных разновидностей гексамино и 108 разновидностей гептамино. В число последних включено и одно спорное гептамино, изображенное на рис. 66. В большинстве развлечений с полимино такие фигуры с внутренними «дырками» (в случае октамино их, например, шесть) лучше всего исключать из рассмотрения. 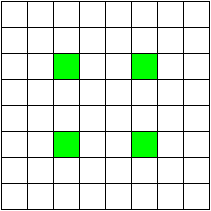 Рис. 67. В главе 3 задача о полимино (задача 3) рассматривалась в связи с расположением домино на шахматной доске с вырезанными углами. В статье Голомба обсуждается много не менее интересных аналогичных задач о полимино высших порядков. Очевидно, что покрыть шахматную доску размером 8x8 клеток одними лишь тримино невозможно (хотя бы потому, что число 64 не делится на 3). Можно ли покрыть ту же доску двадцать одним прямым тримино и одним мономино? С помощью хитроумной раскраски квадратов, из которых состоят кости тримино, в три различных цвета Голомб показал, что это возможно лишь тогда, когда мономино закрывает один из заштрихованных квадратов на рис. 67. С другой стороны, методом полной математической индукции можно доказать, что двадцать одним тримино и одним мономино можно полностью покрыть шахматную доску независимо от того, где находится мономино. Оказывается, доску можно покрыть и шестнадцатью одинаковыми тетрамино любого типа, кроме зигзагообразного. Зигзагообразные тетрамино нельзя уложить даже так, чтобы закрыть хотя бы полоску у края доски. Если доску раскрасить разноцветными полосками, то можно доказать, что 15 L-образных тетрамино и одно квадратное тетрамино не могут образовывать покрытия. Раскрасив доску полосами в виде зигзагов, мы докажем, что квадратное тетрамино плюс любая комбинация прямых и зигзагообразных тетрамино также не могут покрывать целиком всю доску. При взгляде на пентамино, изображенные на рис. 65, невольно возникает вопрос: можно ли из этих 12 фигур и одного квадратного тетрамино сложить обычную шахматную доску размером 8x8 клеток? Впервые решение этой задачи появилось в 1907 году. Оно принадлежало Генри Дьюдени**. В решении Дьюдени квадратное тетрамино примыкает к боковой стороне доски. Лет через двадцать читатели английского журнала «Небывалые шахматы» (под небывалыми, или фантастическими, шахматами здесь подразумеваются игры на необычных досках с необычными фигурами и по необычным правилам) начали исследовать разные пентамино и гексамино. Самые интересные результаты были опубликованы в декабрьском номере того же журнала за 1954 год. Многое из того, о чем здесь будет рассказано, взято из этого номера и из неопубликованной статьи Голомба, посвященной аналогичным теоремам, которые он доказал независимо от других. 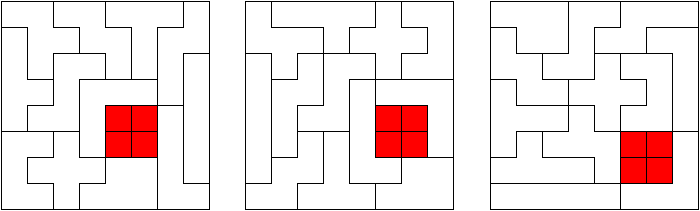 Рис. 68. Доказательство Т.Р. Доусона. Т. Р. Доусон, основатель журнала «Небывалые шахматы», первым придумал удивительно простой способ доказательства того, что задача Дьюдени имеет решение при любом положении квадрата. Три варианта его решения представлены на рис. 68. Квадратное тетрамино в комбинации с L-образным пентамино образует квадрат 3x3. При вращении большого квадрата квадратичное пентамино на каждом рисунке оказывается в четырех различных положениях. Шахматную доску можно вращать как целое и отражать в зеркале, поэтому легко видеть, что квадратное тетрамино может находиться в любом месте доски. Никто не знает, сколько всего существует решений этой задачи, но похоже, что их больше 10 000. В 1958 году Дана С. Скотт (аспирантка-математик из Принстона) с помощью компьютера нашла все возможные решения с квадратом в центре доски. За три с половиной часа компьютер выдал полный список из 65 различных решений (решения, получаемые одно из другого при поворотах и отражениях доски, не считаются различными и входят в этот список как одно решение). 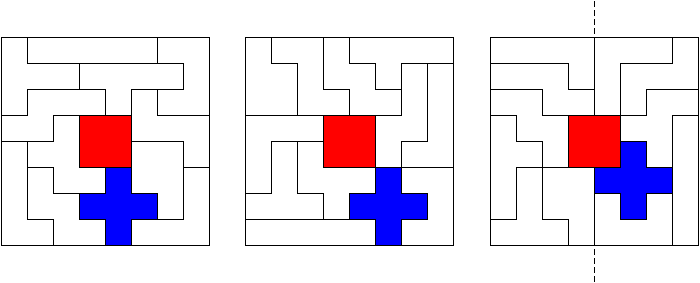 Рис. 69. При составлении программы было удобно разбить все решения на три класса в зависимости от расположения креста относительно центрального квадрата. На рис. 69 показаны решения всех трех классов. Компьютер нашел 20 решений первого, 19 второго и 26 третьего классов. Исследуя все 65 решений, мы обнаруживаем несколько интересных фактов. Не существует решения, в котором прямое тетрамино не прилегало бы по всей своей длине к стороне доски. Для решений, в которых квадрат расположен не в центре, это утверждение неверно. В семи решениях (принадлежащих к первому и третьему классам) нет «перекрестков», то есть точек, где бы соприкасались углы четырех фигур. Отдельные знатоки считают, что «перекрестки» портят красоту рисунка. У третьего решения (рис. 69) есть интересное свойство: фигуру можно перегнуть пополам вдоль прямой линии. Существует 12 таких решений, все они относятся к третьему классу, и у каждого есть «перекрестки». 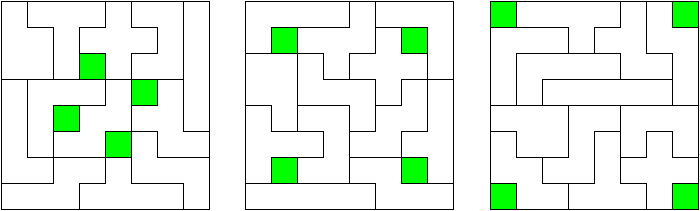 Рис. 70. Если не использовать квадратичное тетрамино и оставить незакрытыми четыре клетки в различных местах шахматной доски, то остальную часть ее можно будет собрать многими способами. Такая «неполная» доска выглядит довольно изящно (три варианта сборки показаны на рис. 70). 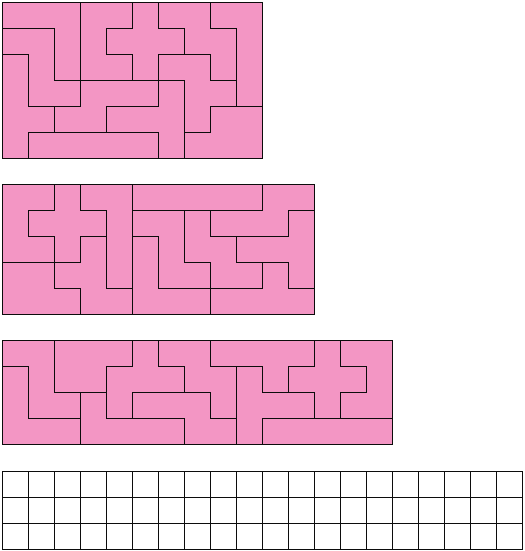 Рис. 71. Прямоугольники, составленные из пентамино. Из двенадцати пентамино можно сложить прямоугольники 6 х 10; 5 х 12; 4 х 15 и 3 х 20 (рис. 71). Прямоугольник 3 х 20, со всех точек зрения более сложный, мы предлагаем интересующемуся читателю собрать самостоятельно. Существует только два различных решения этой задачи, если не считать вращений и отражений. 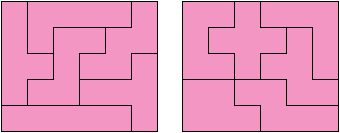 Рис. 72. Обратите внимание, что на рис. 71 прямоугольник 5 х 12 собран из двух прямоугольников 5 х 7 и 5 х 5. Два прямоугольника 5 x 6, изображенные на рис. 72, можно сложить так, что получится прямоугольник либо 5 х 12, либо 6 х 10. Профессор Р. Робинсон и Дж. Таккер независимо друг от друга придумали задачу, которая получила название задачи об утроении. Выбрав одно из пентамино, нужно с помощью девяти остальных фигур построить большую фигуру, подобную выбранной. Фигура должна быть в три раза выше и шире, чем первоначальная. Задача об утроении допускает много изящных решений, три из них показаны на рис. 73. Задача об утроении решается для любого из двенадцати пентамино. 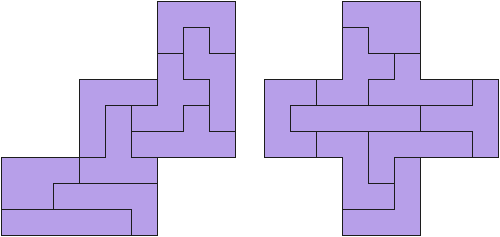 Рис. 73. Схемы утроения. 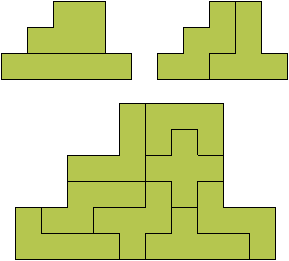 Рис. 74. Схемы «двойного удвоения». 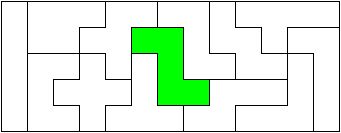 Рис. 75. Не менее интересны и другие задачи на составление различных фигур из «костей» пентамино, например «задача о двойном удвоении». Сначала вы складываете два пентамино. Потом строите эту фигуру из двух других пентамино, а из восьми оставшихся пентамино складываете подобную фигуру, но вдвое больших размеров. Типичное решение такой задачи показано на рис. 74. Другая задача состоит в том, чтобы из всех 12 фигур пентамино сложить прямоугольник 5 х 13, имеющий в центре отверстие в форме одной из этих фигур. Задача решается всегда независимо от того, с какой из 12 фигур пентамино совпадает форма отверстия. Одно из решений приведено на рис. 75. 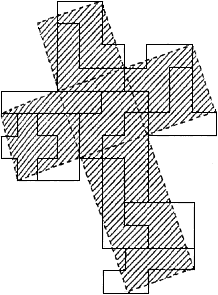 Рис. 76. Развертка куба, сложенная из пентамино. На рис. 76 показана еще одна интересная задача. Из двенадцати пентамино требуется сложить развертку куба с ребром, равным √10. Куб получается, если рисунок согнуть по пунктирным линиям. Какое минимальное число пентамино надо положить на шахматную доску, чтобы ни для одного из оставшихся пентамино места больше не было? Этот любопытный вопрос придумал Голомб; сам он считает, что это число равно пяти. 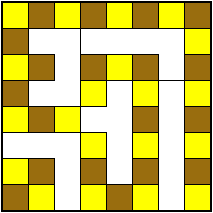 Рис. 77. Игра на шахматной доске фигурами пентамино. На рис. 77 изображена одна из таких конфигураций. Эта задача натолкнула Голомба на мысль играть на шахматной доске картонными пентамино, вырезанными точно по размерам квадратов доски. (Мы рекомендуем читателю изготовить такой набор пентамино, ибо он годен не только для игры, но и для того, чтобы решать и придумывать задачи.) Двое или более игроков по очереди выбирают любое пентамино и закрывают им любые клетки доски. У фигур нет «верхней» и «нижней» стороны. Как и во всех других задачах этой главы, пентамино могут быть асимметричными. Проигрывает тот, кто не сможет поставить свое пентамино. Голомб пишет: «Игра продолжается не менее пяти и не более двенадцати ходов, никогда не заканчивается вничью, в начале партии отличается большим разнообразием, чем шахматы, и наверняка увлечет людей самого различного возраста. Давать советы относительно стратегии игры трудно, но два важных принципа все же можно указать: 1. Старайтесь играть так, чтобы всегда оставалось место для четного числа «костей» (если вы играете вдвоем). 2. Если вы затрудняетесь проанализировать создавшуюся позицию, постарайтесь по возможности усложнить ее, чтобы противник оказался в еще более затруднительном положении, чем вы». Поскольку 35 костей гексамино покрывают площадь в 210 квадратиков, невольно возникает мысль: а нельзя ли сложить из них прямоугольники размером 3 х 70, 5 х 42, 6 х 35, 7 х 30, 10 х 21 или 14 х 15? Я всерьез подумывал о том, чтобы назначить премию в 1000 долларов тому из читателей, кто сумеет построить один из этих шести прямоугольников, но мысль о тех долгих часах, которые ему придется затратить понапрасну, чтобы отыскать решение, вынудила меня отказаться от моего намерения. Дело в том, что все подобные попытки, как доказал Голомб, заранее обречены на провал. Его доказательство может служить прекрасным примером использования методов комбинаторной геометрии — мало известной отрасли математики, выводы которой широко используются в технике при отыскании оптимальных способов подгонки стандартных деталей. Для нас особый интерес представляют два примера: а) раскраска частей интересующей нас фигуры в различные цвета для большей наглядности; б) принцип «проверки на четность», основанный на использовании комбинаторных свойств четных и нечетных чисел. Прежде всего раскрасим наши прямоугольники подобно шахматной доске в черные и белые квадраты. И тех и других должно быть нечетное число: 105 черных квадратов и 105 белых. Перебрав 35 фигур гексамино, мы обнаружим, что 24 из них всегда покрывают три черных и три белых квадрата, то есть нечетное число квадратов каждого цвета. Число таких «нечетных гексамино» четно, а поскольку произведение четного числа на нечетное четно, мы можем утверждать, что все вместе 24 «четных» гексамино покроют четное число квадратов каждого цвета. 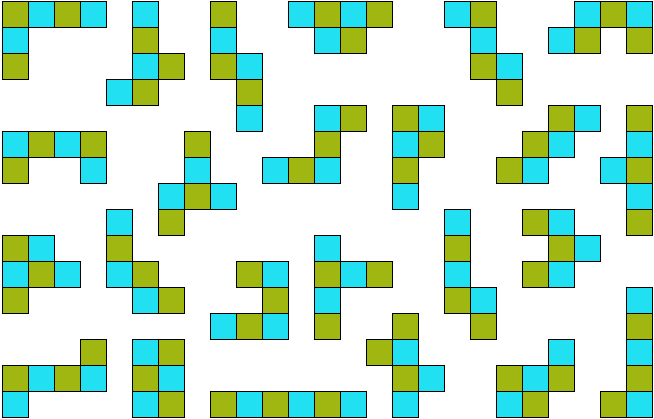 Рис. 78. Двадцать четыре «нечетных» гексамино. 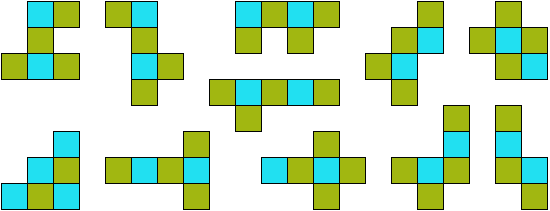 Рис. 79. Двадцать четыре «четных» гексамино. Остающиеся 11 гексамино имеют такую форму, что каждым из них можно накрыть четыре квадрата одного цвета и два другого, то есть четное число квадратов того и другого цвета. Число таких «четных гексамино» нечетно, но опять же, поскольку произведение четного числа на нечетное есть число четное, мы можем с уверенностью утверждать, что эти 11 фигур накрывают четное число квадратов каждого цвета. (На рис. 78 и 79 разбиты на группы 35 гексамино четных и нечетных фигур.) Наконец, поскольку сумма четных чисел четна, мы заключаем, что с помощью 35 гексамино можно накрыть четное число белых квадратов и четное число черных. К сожалению, каждый прямоугольник состоит из 105 квадратов каждого цвета. Это число нечетно, поэтому прямоугольника, который можно было покрыть 35 фигурами гексамино, не существует. «Рассмотренные задачи, — резюмирует Голомб, — заставляют сделать вывод, который относится ко всем правдоподобным рассуждениям вообще. Взяв те или иные начальные данные, мы долго и упорно пытаемся подогнать их под некоторую схему. Если это нам удается, мы считаем, что только такая схема и «соответствует фактам». В действительности же те данные, которыми мы располагаем, отражают лишь отдельные стороны прекрасного и всеобъемлющего целого. Такого рода рассуждения неоднократно встречаются в религии, политике и даже в науке. Пентамино служит примером того, как одни и те же данные с одинаковым успехом удовлетворяют многим различным схемам. Схема, на которой мы в конце концов останавливаем свой выбор, определяется не столько имеющимися в нашем распоряжении данными, сколько тем, к чему мы стремимся. Вполне возможно, что при некоторых данных (как это было в задаче о прямоугольниках, составленных из гексамино) схемы, которую мы так стремимся отыскать, вообще не существует». * * * 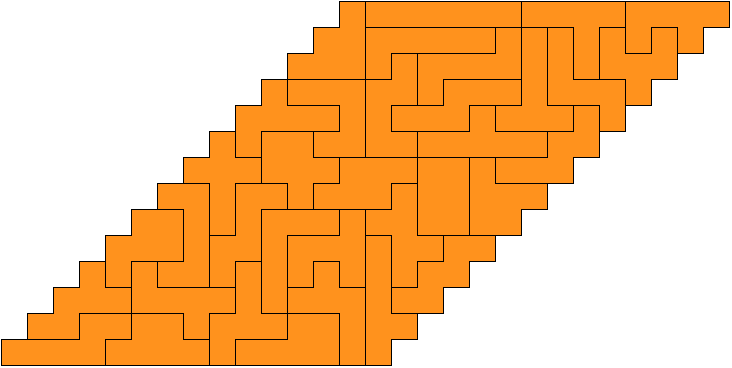 Рис. 80. Фигура I для складывания из гексамино.  Рис. 81. Фигура II для складывания из гексамино. Читателям, которые захотят попробовать свои силы в складывании фигур из гексамино, можно предложить еще два примера (рис. 80 и 81), заимствованных из журнала «Небывалые шахматы». Каждая из фигур составлена из полного набора (35 костей) гексамино. Построить же фигуры из полного набора гексамино можно лишь в том случае, если разность между числом квадратов одного и другого цвета равна 2, 6, 10, 14, 18 и 22.
| |
| Просмотров: 7483 | Комментарии: 1 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта