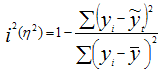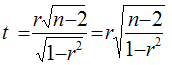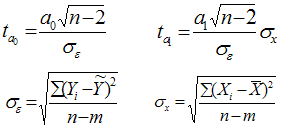| Главная » Статьи » Математика » Математика |
| Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. При анализе адекватности уравнения регрессии (модели) исследуемому процессу, возможны следующие варианты: 1. Построенная модель на основе F-критерия Фишера в целом адекватна и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений и осуществления прогнозов. 2. Модель по F-критерию Фишера адекватна, но часть коэффициентов не значима. Модель пригодна для принятия некоторых решений, но не для прогнозов. 3. Модель по F-критерию адекватна, но все коэффициенты регрессии не значимы. Модель полностью считается неадекватной. На ее основе не принимаются решения и не осуществляются прогнозы. Корреляционный и регрессионный анализ, как правило, проводится для ограниченной по объёму совокупности. Поэтому показатели регрессии и корреляции – параметры уравнения регрессии, коэффициент корреляции и коэффициент детерминации могут быть искажены действием случайных факторов. Чтобы проверить, на сколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Чтобы иметь общее суждение о качестве модели, из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации. Проверка адекватности уравнения регрессии (модели) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 10-12% (рекомендовано).
Оценка значимости уравнения регрессии в целом производится на основе F-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной (y) от среднего значения (yср.) раскладывается на две части – «объясненную» и «необъясненную»:
Схема дисперсионного анализа имеет следующий вид (n –число наблюдений, m–число параметров при переменной x):
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия Фишера. Фактическое значение F -критерия Фишера сравнивается стабличным значением Fтабл. (α, k1, k2) при заданном уровне значимости α и степенях свободы k1= m и k2=n-m-1. При этом, если фактическое значение F-критерия больше табличного Fфакт > Fтеор, то признается статистическая значимость уравнения в целом. Для парной линейной регрессии m=1 , поэтому:
Эта формула в общем виде может выглядеть так:
Отношение объясненной части дисперсии переменной (у) к общей дисперсии называют коэффициентом детерминации и используют для характеристики качества уравнения регрессии или соответствующей модели связи. Соотношение между объясненной и необъясненной частями общей дисперсии можно представить в альтернативном варианте:
Коэффициент детерминации R2 принимает значения в диапазоне от нуля до единицы 0≤ R2 ≤1. Коэффициент детерминации R2 показывает, какая часть дисперсии результативного признака (y) объяснена уравнением регрессии.Чем больше R2, тем большая часть дисперсии результативного признака (y) объясняется уравнением регрессии и тем лучше уравнение регрессии описывает исходные данные. При отсутствии зависимости между (у) и (x) коэффициент детерминации R2 будет близок к нулю. Таким образом, коэффициент детерминации R2 может применяться для оценки качества (точности) уравнения регрессии. Возникает вопрос, при каких значениях R2 уравнение регрессии следует считать статистически незначимым, что делает необоснованным его использование в анализе? Ответ на этот вопрос дает F - критерий Фишера Fфакт > Fтеор - делаем вывод о статистической значимости уравнения регрессии. Величина F - критерия связана с коэффициентом детерминации R2xy (r2xy), и ее можно рассчитать по следующей формуле:
Либо при оценке значимости индекса (аналог коэффициента) детерминации:
Использование коэффициента множественной детерминации R2 для оценки качества модели, обладает тем недостатком, что включение в модель нового фактора (даже несущественного) автоматически увеличивает величину R2. Поэтому, при большом количестве факторов, предпочтительнее использовать, так называемый, улучшенный, скорректированный коэффициент множественной детерминации R2, определяемый соотношением: где p – число факторов в уравнении регрессии, n – число наблюдений. Чем больше величина p, тем сильнее различия между множественным коэффициентом детерминации R2 и скорректированным R2. При использовании скорректированного R2, для оценки целесообразности включения фактора в уравнение регрессии, следует учитывать, что увеличение его величины (значения), при включении нового фактора, не обязательно свидетельствует о его значимости, так как значение увеличивается всегда, когда t-статистика больше единицы (|t|>1). При заданном объеме наблюдений и при прочих равных условиях, с увеличением числа независимых переменных (параметров), скорректированный коэффициент множественной детерминации убывает. При небольшом числе наблюдений, скорректированная величина коэффициента множественной детерминации R2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель. Низкое значение коэффициента множественной корреляции и коэффициента множественной детерминации R2 может быть обусловлено следующими причинами: в регрессионную модель не включены существенные факторы; неверно выбрана форма аналитической зависимости, не реально отражающая соотношения между переменными, включенными в модель. Для оценки значимости парного коэффициента корреляции (корень квадратный из коэффициента детерминации), при условии линейной формы связи между факторами, можно использовать t-критерий Стьюдента:
При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n<30) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия для параметров a0 а1:
n-число наблюдений, m-число параметров уравнения регрессии, σε-(остаточное) среднее квадратическое отклонение результативного признака от выровненных значений ŷ; σх-среднее квадратическое отклонение факторного признака от общей средней. Вычисленные, по вышеприведенным формулам, значения сравнивают с критическими t, которые определяют по таблице значений Стьюдента с учетом принятого уровня значимости α и числа степеней свободы вариации k (ν)=n-2. В социально-экономических исследованиях уровень значимости α обычно принимают равным 0,05. Параметр признаётся значимым (существенным) при условии, если tрасч. > tтабл. В этом случае, практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. | |
| Просмотров: 29771 | Комментарии: 1 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |

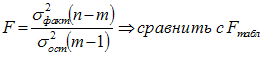
 где: i
где: i