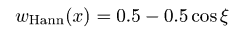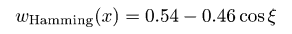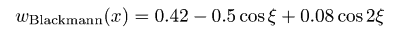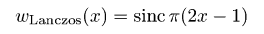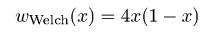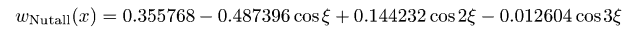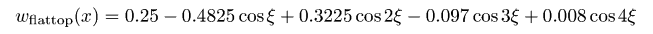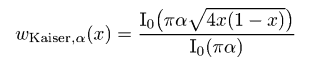$AlexLat$

Преобразование Фурье

Двумерное преобразование Фурье доступно через меню Обработка данных →

  Интегральные преобразования → 2D БПФ, где реализовано быстрое преобразование

 Фурье (БПФ, FFT). Преобразование Фурье раскладывает сигнал на его гармонические

 составляющие, и, таким образом, его можно использовать при изучении спектральных

 частот, присутствующих в данных СЗМ.

Модуль 2D FFT предоставляет несколько типов вывода:

и некоторые их комбинации для удобства.

Радиальные сечения двумерной ФСПМ могут быть с лёгкостью получены с помощью меню 

Обработка данных → Статистика → Сече

Преобразование Фурье

ние ФСПМ. Некоторые другие функции, расчитывающие спектральные плотности, описаны в разделе  Статистический анализ.Также возможно фильтровать изображения в частотных интервалах используя одномерную   или  двумерную фильтрацию БПФ.

Следует отметить, что преобразование Фурье считает данные бесконечно протяженными, и,

 следовательно. накладывает некоторые периодические граничные условия. Поскольку

 реальные данные не обладают этими свойствами, необходимо использовать некоторую 

оконную функцию для выравнивания данных на границах изображения. Если вы этого не

 сделаете, БПФ будет считать данные обработанными прямоугольной функцией окна, которая

 имеет действительно плохой Фурье-образ, что приводит к искажению Фурье-спектра.

Gwyddion предлагает на выбор несколько функций окна. Большинство из них образовано 

набором синусов и косинусов, которые корректно приглушают данные на краях. В следующей 

 таблице оконных формул независимая переменная x лежит в диапазоне [0, 1], что 

соответствует нормализации абсциссы; для простоты переменная ξ = 2πx используется в

 ряде формул. Доступные виды оконных функцию включают в себя:

Название	Формула
Нет	1
Прямоугольное	0.5 в граничных точках, 1 во всех остальных
Ханн
Хэмминг
Блэкмен
Ланцош
Велч
Наттолл
Плоская вершина
Кайзер α	where I0 is the modified Bessel function of zeroth order and α is a parameter

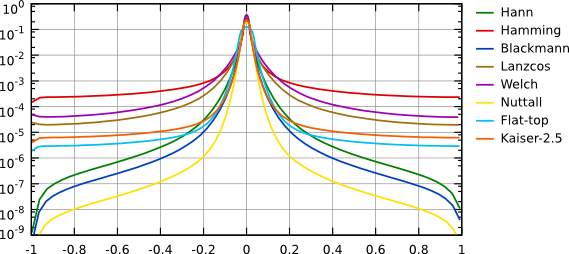Оконные функции: Ханна, Хэмминга, Блэкмена, Ланцоша, Велча, Наттола, с плоской вершиной, Кайзера 2,5.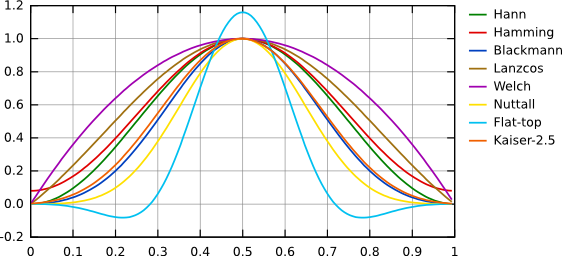

Огибающие частотного отклика оконных функций: Ханна, Хэмминга, Блэкмена, Ланцоша, Велча, Наттола, с плоской вершиной, Кайзера 2,5.

Преобразования Фурье данных с размерами, которые не раскладываются на малые простые числа могут быть очень медленными – и многие программы реализуют БПФ только для массивов, размер которых кратен степени двух.

В Gwyddion, тем не менее, преобразование Фурье может использоваться к полям данных и линиям произвольного размера, без использования передискретизации данных (по крайней мере начиная с версии 2.8). Преобразования Фурье рассчитываются либо с использованием знаменитой библиотеки FFTW  либо, если она недоступна, используя встроенные в Gwyddion функции, которые работают медленнее, но так же могут работать с данными произвольной длины.

Тем не менее, если размер данных не раскладывается на малые простые числа, преобразование работает заметно медленнее. Следовательно, желательно преобразовывать поля данных