Уравнение цен и его аналитическое решение. Только что описанная
ситуация представлена графически на рис.5. Пусть q -размер партии, ts
- интервал времени между запусками в производство партии, а R - полный спрос за
всё времени планирования T.
 Тогда R/q – число партий за время Т и
Если интервал ts начинается, когда на кладе имеется q изделий и заканчивается
при.
Тогда R/q – число партий за время Т и
Если интервал ts начинается, когда на кладе имеется q изделий и заканчивается
при.
 отсутствии заказов, тогда q/2 – средний запас в течение ts (равенство
q/2= qср следует рассматривать как приближенное. Точность его тем выше, чем
больше R) q/2* C1 ts затраты на хранения в интервале ts.
Общая стоимость создания запасов в интервале ts равна сумме стоимости запуска
в производство
отсутствии заказов, тогда q/2 – средний запас в течение ts (равенство
q/2= qср следует рассматривать как приближенное. Точность его тем выше, чем
больше R) q/2* C1 ts затраты на хранения в интервале ts.
Общая стоимость создания запасов в интервале ts равна сумме стоимости запуска
в производство 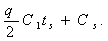 Для вычисления полной стоимости создания запасов за время Т следует эту
величину умножить на общее число партий за это время:
Для вычисления полной стоимости создания запасов за время Т следует эту
величину умножить на общее число партий за это время:
 Подставляя сюда выражение для ts, получаем
Подставляя сюда выражение для ts, получаем
 или
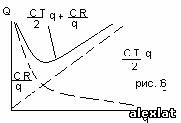
Члены в правой части уравнений (44) представляют стоимость хранения и полную
стоимость заказа в производстве всех партий. С увеличением размера партий
первый член возрастает, а второй убывает. Решение задачи управления запасами
и состоит в определении такого размера партии qo, при котором суммарная
стоимость была бы наименьшей (рис. 6)
или
Члены в правой части уравнений (44) представляют стоимость хранения и полную
стоимость заказа в производстве всех партий. С увеличением размера партий
первый член возрастает, а второй убывает. Решение задачи управления запасами
и состоит в определении такого размера партии qo, при котором суммарная
стоимость была бы наименьшей (рис. 6)
 Найденное оптимальное значение qo размер партии
Найденное оптимальное значение qo размер партии

 Для оптимальных tsо и Qo имеем
Пример I: Пусть предприниматель должен поставлять своему заказчику 24000
единиц продукции в год. Так как получаемая продукция используется
непосредственно на сборочной линии и заказчик не имеет для нее специальных
складов, поставщик должен единично отгружать дневную норму. В случаи нарушения
поставок поставщик рискует потерять заказ. Поэтому нехватка продукции
недопустима, т.е. штраф при нехватке можно бесконечным. Хранение единицы
продукции в месяц стоит 0,1 долл. Стоимость запуска в производство одной партии
продукции составляет 350 долл.
Требуется определить оптимальный размер партии q0, оптимальный период и tsо
вычислить минимум общих ожидаемых годовых затрат Qо. В данном случае Т = 12
месяцам, R = 24 000 единиц, Сs = 0,1 долл./партия Сs = 350 дол/партия.
Подстановка этих значений в уравнения (9), (10) и (11) дает нам.
Для оптимальных tsо и Qo имеем
Пример I: Пусть предприниматель должен поставлять своему заказчику 24000
единиц продукции в год. Так как получаемая продукция используется
непосредственно на сборочной линии и заказчик не имеет для нее специальных
складов, поставщик должен единично отгружать дневную норму. В случаи нарушения
поставок поставщик рискует потерять заказ. Поэтому нехватка продукции
недопустима, т.е. штраф при нехватке можно бесконечным. Хранение единицы
продукции в месяц стоит 0,1 долл. Стоимость запуска в производство одной партии
продукции составляет 350 долл.
Требуется определить оптимальный размер партии q0, оптимальный период и tsо
вычислить минимум общих ожидаемых годовых затрат Qо. В данном случае Т = 12
месяцам, R = 24 000 единиц, Сs = 0,1 долл./партия Сs = 350 дол/партия.
Подстановка этих значений в уравнения (9), (10) и (11) дает нам.
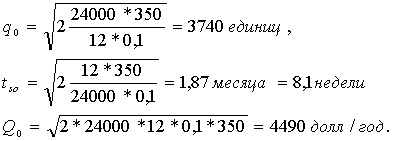 Модель II.
Рассмотрим теперь случай, который отличается от предыдущего только тем, что
превышение спроса над запасами уже допускается, т.е. штраф за нехватку
конечный.
Модель II.
Рассмотрим теперь случай, который отличается от предыдущего только тем, что
превышение спроса над запасами уже допускается, т.е. штраф за нехватку
конечный.
|  Тогда R/q – число партий за время Т и
Если интервал ts начинается, когда на кладе имеется q изделий и заканчивается
при.
Тогда R/q – число партий за время Т и
Если интервал ts начинается, когда на кладе имеется q изделий и заканчивается
при.
 отсутствии заказов, тогда q/2 – средний запас в течение ts (равенство
q/2= qср следует рассматривать как приближенное. Точность его тем выше, чем
больше R) q/2* C1 ts затраты на хранения в интервале ts.
Общая стоимость создания запасов в интервале ts равна сумме стоимости запуска
в производство
отсутствии заказов, тогда q/2 – средний запас в течение ts (равенство
q/2= qср следует рассматривать как приближенное. Точность его тем выше, чем
больше R) q/2* C1 ts затраты на хранения в интервале ts.
Общая стоимость создания запасов в интервале ts равна сумме стоимости запуска
в производство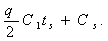 Для вычисления полной стоимости создания запасов за время Т следует эту
величину умножить на общее число партий за это время:
Для вычисления полной стоимости создания запасов за время Т следует эту
величину умножить на общее число партий за это время:
 Подставляя сюда выражение для ts, получаем
Подставляя сюда выражение для ts, получаем
 или
Члены в правой части уравнений (44) представляют стоимость хранения и полную
стоимость заказа в производстве всех партий. С увеличением размера партий
первый член возрастает, а второй убывает. Решение задачи управления запасами
и состоит в определении такого размера партии qo, при котором суммарная
стоимость была бы наименьшей (рис. 6)
или
Члены в правой части уравнений (44) представляют стоимость хранения и полную
стоимость заказа в производстве всех партий. С увеличением размера партий
первый член возрастает, а второй убывает. Решение задачи управления запасами
и состоит в определении такого размера партии qo, при котором суммарная
стоимость была бы наименьшей (рис. 6)
 Найденное оптимальное значение qo размер партии
Найденное оптимальное значение qo размер партии

 Для оптимальных tsо и Qo имеем
Пример I: Пусть предприниматель должен поставлять своему заказчику 24000
единиц продукции в год. Так как получаемая продукция используется
непосредственно на сборочной линии и заказчик не имеет для нее специальных
складов, поставщик должен единично отгружать дневную норму. В случаи нарушения
поставок поставщик рискует потерять заказ. Поэтому нехватка продукции
недопустима, т.е. штраф при нехватке можно бесконечным. Хранение единицы
продукции в месяц стоит 0,1 долл. Стоимость запуска в производство одной партии
продукции составляет 350 долл.
Требуется определить оптимальный размер партии q0, оптимальный период и tsо
вычислить минимум общих ожидаемых годовых затрат Qо. В данном случае Т = 12
месяцам, R = 24 000 единиц, Сs = 0,1 долл./партия Сs = 350 дол/партия.
Подстановка этих значений в уравнения (9), (10) и (11) дает нам.
Для оптимальных tsо и Qo имеем
Пример I: Пусть предприниматель должен поставлять своему заказчику 24000
единиц продукции в год. Так как получаемая продукция используется
непосредственно на сборочной линии и заказчик не имеет для нее специальных
складов, поставщик должен единично отгружать дневную норму. В случаи нарушения
поставок поставщик рискует потерять заказ. Поэтому нехватка продукции
недопустима, т.е. штраф при нехватке можно бесконечным. Хранение единицы
продукции в месяц стоит 0,1 долл. Стоимость запуска в производство одной партии
продукции составляет 350 долл.
Требуется определить оптимальный размер партии q0, оптимальный период и tsо
вычислить минимум общих ожидаемых годовых затрат Qо. В данном случае Т = 12
месяцам, R = 24 000 единиц, Сs = 0,1 долл./партия Сs = 350 дол/партия.
Подстановка этих значений в уравнения (9), (10) и (11) дает нам.
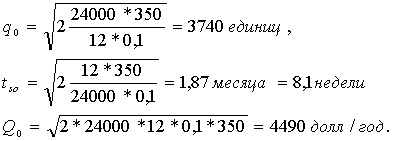 Модель II.
Рассмотрим теперь случай, который отличается от предыдущего только тем, что
превышение спроса над запасами уже допускается, т.е. штраф за нехватку
конечный.
Модель II.
Рассмотрим теперь случай, который отличается от предыдущего только тем, что
превышение спроса над запасами уже допускается, т.е. штраф за нехватку
конечный.