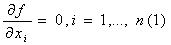Безусловный и условный экстремумы
Важное место в математиком аппарате экономики занимают оптимальные задачи –
задачи, которых ищется наилучшее в определенном смысле решение. В
экономической практике требуется использовать имеющиеся ресурс наиболее
выгодным образом. В экономической теории одним из отправных пунктов является
постулат о том, что каждый экономический субъект, имея определенную свободу
выбора своего поведения, отыскивает наилучший со своей точки зрения вариант.
И оптимизационные задачи служат средством описания поведения экономических
субъектов, инструментом исследования закономерностей этого поведения.
Многие задачи оптимизации формулируются следующим образом. Решение, которое
должен принять субъект, описывается набором чисел х1 ,х2 ,.,хn (или точкой
Х=(х1 ,х2 ,.,хn) n-мерного пространства). Достоинства того или иного решения
определяются значениями функция f(X) = f(х1, х2 ,.,хn) — целевой функции
. Наилучшее решение — это такая точка Х, в которой функция f(Х) принимает
наибольшее значение. Задача нахождения такой точки описывается следующим
образом:
f(X) ® max.
Если функция f(X) характеризует отрицательные стороны решения (ущерб, убытки
и т. п.), то ищется точка Х, в которой значение f(X) минимально:
f(X) ® min.
Минимум и максимум объединяются понятием экстремума. Для определенности мы
будем говорить только о задачах максимизации. Поиск минимума не требует
специального рассмотрения, поскольку заменой целевой функции f(X) на -f(Х)
всегда можно "превратить недостатки в достоинства” и свести минимизацию к
максимизации.
Из каких вариантов должен быть выбран наилучший? Иными словами, среди каких
точек пространства нужно искать оптимум. Ответ на этот вопрос связан с таким
элементом оптимизационной задачи, как множество допустимых решений. В
некоторых задачах допустимыми являются любые комбинации чисел х1, х2,.,хn то
есть множество допустимых решений - это все рассматриваемое пространство.
В других задачах следует принимать во внимание различные ограничения,
означающие, что не все точки пространства доступны при выборе. В
содержательных постановках задач это может быть связано, например, с
ограниченностью располагаемого количества ресурсов.
Ограничения могут быть представлены в форме равенств вида
g(X) = О
или неравенства
g(X) ³ О.
Если условия имеют несколько другую форму, скажем, g1(Х) = g2(X) или g(X)
£ A, то их можно привести к стандартному виду, перенеся в функции и
константы в одну из частей равенства или неравенства.
Экстремум, отыскиваемый во всем пространстве, без каких-либо ограничивающих
условий, носит название безусловного. Если целевая функция непрерывно
дифференцируема, то, необходимое условие безусловного экстремума функции
состоит в равенстве нулю всех ее частных производных:
Если же заданы ограничения, то экстремум ищется лишь среди точек, которые
удовлетворяют всем ограничениям задачи, так как только такие точки являются
допустимыми. В этом случае экстремум носит название условного.
Рассмотрим задачу поиска условного экстремума:
f(X) ® max
при условиях
(2)
g1(Х) = 0; g2(Х) = 0, ., gn(Х) = 0,
все ограничения которой представляют собой равенства.
Если при этом целевая функция и все ограничивающие функции непрерывно
дифференцируемы, то такую задачу мы будем называть задачей Лагранж
а.