| Главная » Файлы » Сканави_ Сборник задач по математике |
| В разделе материалов: 3867 Показано материалов: 2521-2540 |
Страницы: « 1 2 ... 125 126 127 128 129 ... 193 194 » |
|
Решить уравнения x³ - 7x² + 12x - 10 = 0 и x ³- 10x² -2x + 20 = 0,если известно,что один из корней первого уравнения в 2 раза меньше одного из корней второго уравнения |
|
Найти все три корни уравнения ax³ + bx² + cx +d = 0 ,если его коэффициенты удовлетворяют условию ad = bc |
|
Показать, что условие kb² - (k + 1)²ac = 0 (k ≠ 0) является необходимым и достаточным для того ,чтобы отношение корней уравнения ax² + bx +c = 0 было равно k |
|
Решить уравнение ax³ + bx² + cx + d = 0 ,если его коэффициенты a,b,c и d в указанном порядке составляют геометрическую прогрессию с заданным знаменателем q |
|
Доказать,что если корни уравнения x³ + ax² + bx + c = 0 составляют геометрическую прогрессию,то один из них равен - ∛c |
|
Решить уравнение 64x³ - 24x² -6x + 1 = 0,если известно,что его корни образуют геометрическую прогрессию |
|
1. Пусть числа x1,x2 и x3 служат корнями многочлена ax³ + bx² + cx +d . В таком случае имеет место тождеству ax ³+ bx³ + cx +d = a(x -x1)(x - x2)(x- x3) 1. Воспользоваться этим тождеством для получения формул,связывающих корни и коэффициенты данного многочлена 2.С помощью формул,полученных в п1 найти корни x1,x2 и x3 уравнения 8x³ - 20x² - 10x +33 = 0 ,составив и решив новое кубическое уравнение с корнями x1+x2,.x2+x3 и x3+ x1. |
|
Решить уравнение 2ax³ -(2a² +a +2)x² +(a² + 3a +1)x -a = 0,если известно, что произведение двух его корней равно 1 |
|
Составить уравнение с целыми коэффициентами возможно более низкой степени,один из корней которого было бы число √2 +√3. |
|
Показать,что корни уравнения x + x¯¹ = 2cos 40° являются также корнями уравнения x⁴+ x¯⁴ = 2cos160° |
|
Решить уравнение x⁴ - 4x + 3x³ + 8x² - 10 = 0 ,если известно,что два его корня отличаются друг от друга только знаком. |
|
Решить уравнение 2x⁵ - x⁴ - 2x³ + x² - 4x + 2 = 0 ,если известно,что оно имеет три корня,из которых два являются противоположными числами(противоположными называются два числа,сумма которых равна нулю) |
|
Показать,что уравнение 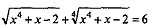 имеет единственный положительный корень,и найти этот корень имеет единственный положительный корень,и найти этот корень |
|
1/log65 1/log87 √25 + 49 |
|
1/log53 log936 4/log79 81 + 27 +3 |
|
- log2log2√∜2 |
|
- log3log3∛∛3 |
|
(27 1/log23 +5 log2549) (811/log4-8 9log49)/3+5 ∙ 5 1/log1625 |
|
36log65+101-lg2-3log9+36 |
|
(81 1/4-1/2log94+25log1258 )•49log72 |
Категории раздела
| Алгебра [52] |
| Тождество [503] |
| Прогрессии [53] |
| Координаты и Вектороы [35] |
| Алгебраические уравнения [250] |
| Логарифмы [348] |
| Тригонометрические уравнения [499] |
| Неравенства [305] |
| Задачи по планиметрии [433] |
| Задачи стереометрии [234] |
| Задачи по Геометрии с применением Тригонометрии [450] |
| Применение уравнений к решению задач [453] |
| Математический Анализ [60] |
| Комбинаторика,Бином Ньютона и Комплексные числа [80] |
| Элементарная математика [112] |
Друзья сайта