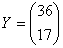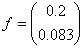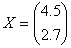| Главная » Статьи » Математика » Алгоритмы |
Построение математической моделиУчитывая характер помехи можно составить следующую имитационную модель системы для формирования реализации вектора и состояния системы на интервале определения: ,
Здесь матрицы коэффициентов модели. t Є [0,T], T = 20 U(t)=15-0 .1t, Здесь [0, T] – интервал определения системы. Уравнение выхода системы: Здесь (параметров) системы. Значение параметров системы: , . Здесь А, В – матрицы коэффициентов (параметров) системы. Характер помехи и ее статистические параметры: Помеха имеет нормальное распределение с математическим ожиданием, равным Алгоритм реализации решения задачи построениядинамической моделиИдея построения требуемой динамической системы состоит в следующем: для заданного значения параметра t с его интервала определения градиентным методом первого порядка находим соответствующее значение параметра x, который изменяется динамически. Поэтому необходимо в каждый момент ti найти оптимальное соответствующее значение фактора х и функции отклика у, которые наиболее близко описывали бы исходную систему. Помеха имеет нормальное распределение, поэтому включаем ее в функцию отклика таким образом, как показано в выше предложенных формулах. Для поиска решения необходимо рассчитать оптимальный шаг ∆t. Это делается по выше указанной формуле ( 6 ) – поиск шага варьирования. Именно так и реализуем в программном решении данной задачи Для поиска оптимального решения используем матрицы коэффициентов модели значение функции отклика. Все выше сказанное реализовано в предлагаемой программе, в которой реализовано решение задачи построения динамической модели в соответствии с заданным типом модели методом идентификации и точностью решения задачи. Программа отлажена на упрощенных тестовых примерах с использованием информации, полученной от имитационной тестовой модели. Проведен анализ полученных результатов, что также отражено в предложенной программе. Апробирование машинной программыКак было отмечено ранее, в данной программе кроме ручного ввода исходных значений факторов X (т. е. задание так называемой «нулевой точки») существует задание количества факторов и количества опытов, как по умолчанию, так и непосредственно пользователем. Программа исследований программного эксперимента: Решает задачу оптимизации поверхности отклика. В начале работы требуется задать значения функции отклика Y, для которых и будет найдены соответствующие значения факторов X , при которых функция отклика принимает максимальное значение.
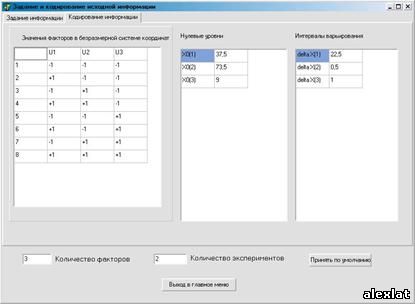
1.Задаем количество факторов и экспериментов Получаем значения факторов в натуральном масштабе, заполняем матрицу планирования. 2.Производим кодирование в безразмерной системе координат, для каждого фактора определяются нулевые уровни и интервалы варьирования. Они будут использованы для определения градиента в данной точке.
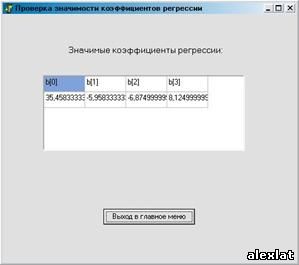
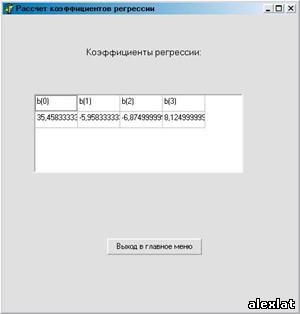
3.Получаем значения коэффициентов регрессии. 4.Считаем выборочные дисперсии, и если они однородны, выводим значение дисперсии воспроизводимости 5.Проверяем на значимость коэффициенты регрессии. В данном случае все коэффициенты значимы. 6. Получаем информацию о том, описывает ли уравнение эксперимент адекватно. 7. Делаем шаг в сторону, противоположную градиенту и находим новую точку (набор факторов). 8. Для нового набора переходим к шагу 2. Выполняем указанные действия до тех пор, пока не приблизимся к точке экстремума, на что указывает убыль последующих значений функции отклика. Результаты работы программыМатрица значений функции отклика системы: . Матрица помех: . Найденные значения факторов, про которых функция отклика принимает максимальное значение:
| |
| Просмотров: 2814 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
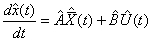
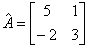
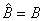
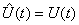
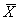 - вектор состояния системы;
- вектор состояния системы; 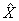 - вектор состояния модели;
- вектор состояния модели; 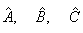 -
-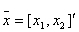 .
.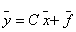 ,
, 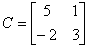 , .
, .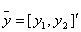
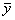 - вектор наблюдения;
- вектор наблюдения; 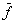 - вектор помехи; C – матрица коэффициентов
- вектор помехи; C – матрица коэффициентов 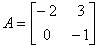
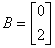
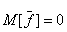 .
.