Фрактальный анализ

Фрактальный анализ

В практике встречаются объекты. которые демонстрируют случайные свойства. Часто предполагается, что в определённом диапазоне масштабов эти объекты демонстрируют свойства аффинного самоподобия. Афинное самоподобие является обобщением самоподобия, которое является основным свойством большинства детерминированных фракталов. Часть афинно-самоподобного объекта подобна целому объекту после анизотропного масштабирования. Многие случайно шероховатые поверхности считаются принадлежащими к классу случайных объектов, которые проявляют свойства аффинного самоподобия и они рассматриваются как афинно-самоподобные статистические фракталы. Разумеется, эти поверхности можно исследовать используя атомно-силовую микроскопию (АСМ). Результаты фрактального анализа аффинно-самоподобных случайных поверхностей с использованием АСМ нередко используются для классификации подобных поверхностей, полученных в результате различных технологических процессов [1.2.3.4.].

В Gwyddion доступны различные виды фрактального анализа в меню Обработка данных → Статистика → Фрактальная размерность.

Метод подсчёта кубов [1.2.]: напрямую выводится из определения фрактальной размерности подсчётом коробок. Алгоритм основан на следующих шагах: кубическая решетка с постоянной решетки l накладывается на растянутую по z поверхность. Вначале l устанавливается на X/2 (где X - половина стороны поверхности), в результате получается решетка из 2×2×2 = 8 кубов. Тогда N(l) - число кубов, которые содержат хотя бы один пиксель изображения. Постоянная решетки l затем последовательно на каждом шаге уменьшается вдвое и процесс повторяется пока l не станет равным расстоянию между двумя соседними пикселями. Наклон графика log(N(l)) от log(1/l) даёт непосредственно фрактальную размерность D_f
Метод триангуляции 1]: весьма похож на алгоритм подсчёта кубов и тоже основан непосредственно на определении фрактальной размерности, основанном на подсчёте коробок. Метод работает следующим образом: сетка с размером ячейки в одну единицу измерения l помещается на поверхность. Это определяет положения вершин набора треугольников. Когда, например, l = X/4, поверхность покрыта 32 треугольниками различной площади наклонёнными под разными углами по отношению к плоскости xy. Площади всех треугольников рассчитываются и суммируются чтобы получить приближенную площадь поверхности S(l), соответствующую l. размер сетки затем уменьшается последовательно в два раза на каждом шаге, как и раньше, процесс продолжается до тех пор. пока l не станет равным расстоянию между двумя соседними точками. Наклон графика S(l) от log(1/l) при этом соответствует D_f − 2.
Вариационный метод [3.4]: основан на зависимости от масштаба фракционного броуновского движения. На практике, в вариационном методе делят полную поверхность на равносторонние квадратные коробки, и вариация (степень среднеквадратичного значения высоты) рассчитывается для заданного размера коробок. Фрактальная размерность рассчитывается из наклона β аппроксимированной методом наименьших квадратов линии на графике в двойном логарифмическом масштабе вариации как D_f = 3 − β/2.
Метод спектра мощности [3.4.5.]: основан на зависимости спектра мощности фракционного броуновского движения. В методе спектра мощности к каждому профилю высоты вдоль линии, из которых состоит изображение применяется преобразование Фурье, рассчитывается спектр мощности и все эти спектры усредняются. Фрактальная размерность определяется из наклона β аппроксимирующей линии, проведённой по методу наименьших квадратов на построенном в двойном логарифмическом масштабе графике спектра мощности, как D_f = 7/2 − β/2.

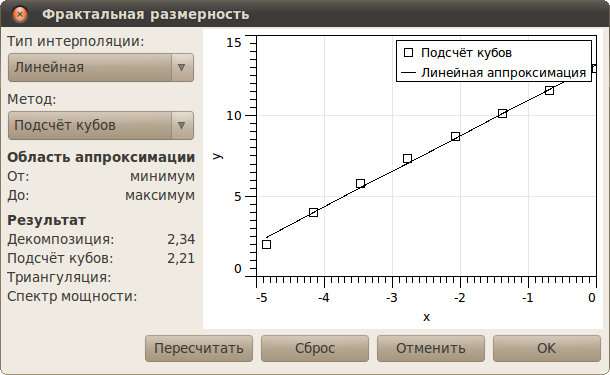
Оси на графиках фрактальной размерности уже приведены к логарифмическому масштабу, следовательно линейные зависимости, упомянутые выше, здесь соответствуют прямым. Единицы измерения осей следует считать произвольными.

Следует отметить, что результаты различных методов различаются. Это явление вызвано систематическими ошибками различных методов фрактального анализа.

Диалоговое окно фрактальной размерности.

Более того, на результат фрактального анализа сильно влияет свёртка с зондом. Мы рекомендуем проверять карту достоверности до начала фрактального анализа. В случае, если поверхность сильно искажена изображением зонда, результаты фрактального анализа могут быть весьма недостоверными.

Следует отметить, что алгоритмы, используемые во фрактальном анализе также используются в модуле фрактальной коррекции и опции инструмента удаления пятен «фрактальная коррекция».