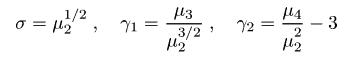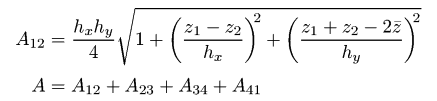Статистический анализ
При
анализе случайно шероховатых поверхностей нередко требуется
статистический подход для определения некоторого набора типичных
величин. В Gwyddion есть несколько различных путей как это можно
сделать. В этом разделе мы опишем различные статистические инструменты и
модули, представленные в Gwyddion, а также представим основные формулы,
которые использовались для разработки лежащих в их основе алгоритмов.
Данные сканирующей зондовой микроскопии обычно представляются как двумерное поле данных размера N×M где N и M – число строк и столбцов поля данных, соответственно. Настоящая площадь этого поля обозначается как Lx×Ly, где Lx и Ly – размеры вдоль соответствующих осей. Интервал дискретизации (расстояние между двумя соседними точками в скане) обозначается Δ. Мы предполагаем, что интервал дискретизации одинаков как в x, так и в y-направлении и что высота поверхности в заданной точке (x, y) может быть описана случайной функцией ξ(x, y) с заданными статистическими свойствами.
Следует заметить, что данные АСМ обычно собираются как линейные сканы вдоль оси x, которые объединяются вместе, чтобы сформировать двумерное изображение. Следовательно, скорость сканирования в направлении x значительно больше, чем скорость сканирования вдоль оси y. В результате, статистические свойства данных АСМ обычно собираются вдоль профилей, параллельных оси x, поскольку на них меньше влияет низкочастотный шум и термический дрейф образца.
Инструмент измерения статистических величин  Статистические
величины включают в себя основные свойства распределения значений
высоты, включая его дисперсию, коэффициент асимметрии и эксцесс.
Следующие величины доступны в меню инструмента Статистические величины программы Gwyddion: - Среднее значение, минимум, максимум, срединное значение.
- Среднеквадратичное значение неровностей высоты: это значение вычисляется из дисперсии данных.
- Ra
значение неровностей высоты: эта величина аналогична
среднеквадратичному значению с единственной разницей в экспоненте
(степени) в сумме отклонений данных. Поскольку для среднеквадратичного
эта экспонента равна q = 2, значение Ra рассчитывается с экспонентой q = 1 и модулем значений данных (нулевым средним).
- Коэффициент асимметрии распределения высот: вычисляется из третьего центрального момента значений данных.
- Эксцесс распределения высот: вычисляется из четвёртого центрального момента значений данных.
- Площадь проекции и площадь поверхности: подсчитывается простой триангуляцией.
- Средний уклон граней в области: вычисляется усреднением нормализованных векторов направления граней.
ПодсказкаПо умолчанию инструмент «Статистические величины» показывает значения для всего изображения. Если вам нужно исследовать определённую область внутри изображения, просто щёлкните мышью и обведите её прямоугольником. Окно инструмента обновится с новыми значениями основанными на новой области. Если вы снова хотите просмотреть статистику для всего изображения, щёлкните один раз на окне данных и инструмент сбросится в исходное состояние..Точнее, среднеквадратичное отклонение (σ), коэффициент асимметрии (γ1), и эксцесс (γ2) вычисляются из центральных моментов i-того порядка μi в соответствии со следующими формулами: 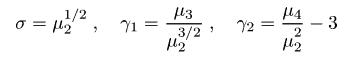
Площадь поверхности оценивается следующим методом. Пусть zi для i = 1, 2, 3, 4 обозначает значения в четырёх соседних точках (центрах пикселей), а hx и hy
- размеры пикселей вдоль соответствующих осей. Если дополнительная
точка помещается в центр прямоугольника который соответствует общему
углу четырёх пикселей (используя среднее значение четырёх пикселей),
образуются четыре треугольника и площадь поверхности может быть
приближенно оценена суммированием их площадей. Это приводит к следующим
формулам для площади одного треугольника (верхняя) и площади поверхности
для одного пикселя (нижняя): 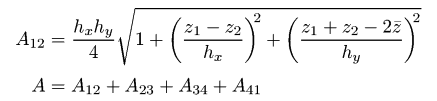
Метод
теперь хорошо определён для внутренних точек области. Каждое значение
участвует в восьми треугольниках, по два с каждым из четырёх соседних
значений. Половина из этих треугольников лежит внутри одного пикселя,
другая половина в другом пикселе. Подсчётом площади, лежащей внутри
каждого пикселя, общая площадь определяется также для зерён и областей
под маской. Осталось определить её для граничных пикселей всего поля
данных. Мы это делаем виртуально расширяя поле данных копией граничного
ряда пикселей с каждой стороны для нужд расчёта площади поверхности,
следовательно делая все интересующие нас пиксели внутренними. 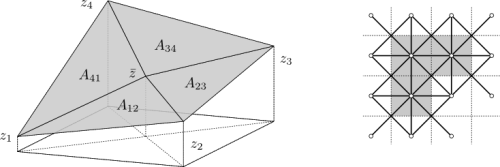
Инструмент статистических функций  Одномерные статистические функции доступны при использовании инструмента Статистические функции. В окне инструмента можно выбрать, какую функцию нужно рассчитать используя выпадающий список слева, озаглавленный Тип вывода.
Предпросмотр графика будет обновляться автоматически. Можно выбрать
направление, в котором будут рассчитываться функции (горизонтальное или
вертикальное), но, как уже говорилось выше, мы рекомендуем использовать
направление быстрой оси сканирования. Также можно выбрать, какой из
методов интерполяции использовать. После того, как выбор закончен, можно нажать кнопку Применить чтобы закрыть окно инструмента и вывести новое окно графика, которое содержит данные статистики. ПодсказкаПодобно инструменту Статистические величины, этот инструмент оценивает по умолчанию всё изображение, но при желании можно выбрать область, на которой будет проводиться анализ |