| Главная » Статьи » Математика » Численные методы оптимизации |
| Формирование оптимального решения двойственной
задачи на основе теоремы о двойственности
Оказывается, что для задач (7.2) - (7.4) и (7.5), (7.6), называемых двойственной парой, справедлива следующая теорема. Теорема (первая теорема о двойственности). Если одна из задач двойственной пары (7.2) - (7.4) и (7.5), (7.6) имеет решение, то
другая задача также разрешима. При этом для любых оптимальных планов
Если линейная форма одной из задач не ограничена (для F(X) – сверху, для f(Y) - снизу), то другая задача не имеет ни одного плана. Оптимальное решение двойственной задачи может быть найдено на основе следующего следствия из этой теоремы. Следствие. Если вектор вектор Стоит отметить, что в ходе решения исходной задачи вторым алгоритмом, при каждом шаге вычисляется вектор
соответствующей основной таблице, находится решение задачи (7.5), (7.6). Пусть двойственная задача имеет вид (7.8), (7.9). Так как исходная задача (2.12), (2.13) имеет решение, то на основании рассмотренной теоремы о двойственности двойственная задача также разрешима. Оптимальным опорным планом исходной является (см. п.4, п.6). При этом ; ; . Вычислим . На основании следствия из теоремы о двойственности можно заключить, что
при котором таблицы (см. табл. 6.3, шаг 5), можно убедиться в том, что оптимальный план двойственной задачи, сформированный на основе теоремы о двойственности, совпадает с оптимальным планом, найденном при решении исходной задачи вторым алгоритмом симплекс-метода. Это говорит о том, что оптимальный план задачи (7.8) - (7.9) найден верно. | |
| Просмотров: 1279 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
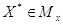 и
и 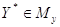 (здесь Мх, Му
– множества планов соответственно прямой и двойственной задач) задач (7.2) - (7.4)
и (7.5), (7.6) имеет место равенство
(здесь Мх, Му
– множества планов соответственно прямой и двойственной задач) задач (7.2) - (7.4)
и (7.5), (7.6) имеет место равенство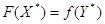
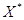 является
оптимальным опорным планом задачи (7.2) - (7.4), то
является
оптимальным опорным планом задачи (7.2) - (7.4), то 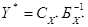 (8.1), является оптимальным
опорным планом задачи (7.5), (7.6).
(8.1), является оптимальным
опорным планом задачи (7.5), (7.6).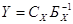 . И если Х – оптимальный
опорный план задачи (7.2) - (7.4), то в (m+1)-й строке,
. И если Х – оптимальный
опорный план задачи (7.2) - (7.4), то в (m+1)-й строке, 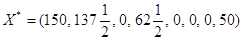
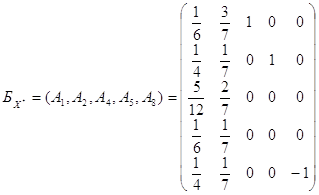
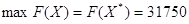
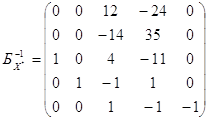
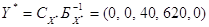 является
оптимальным планом двойственной задачи,
является
оптимальным планом двойственной задачи, 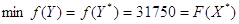 .
Анализируя (m+1)-ю строку основной
.
Анализируя (m+1)-ю строку основной