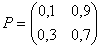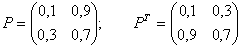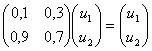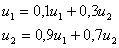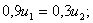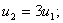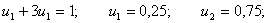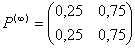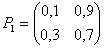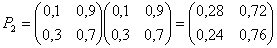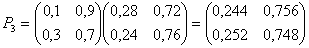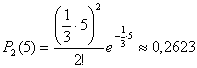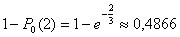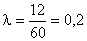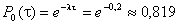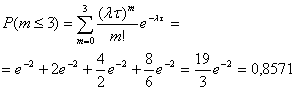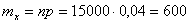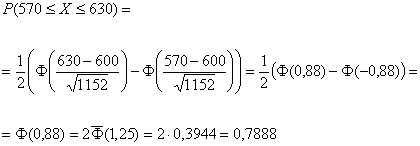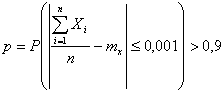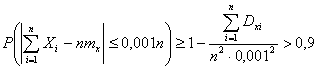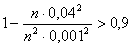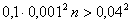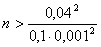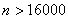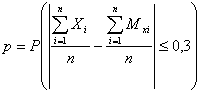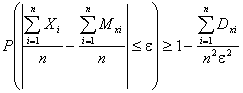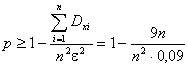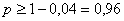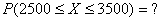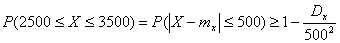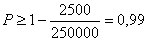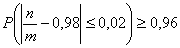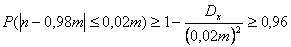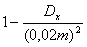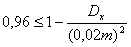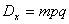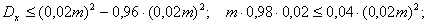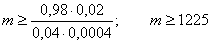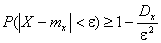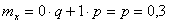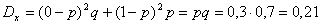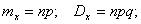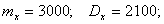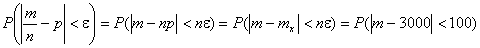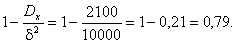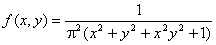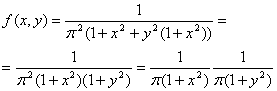$AlexLat$

Предельные вероятности 000302

Задана матрица переходов Р. Найти предельные вероятности



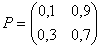
Решение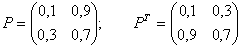

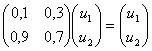
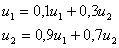
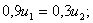
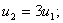
C учетом того, что u₁ + u₂ = 1,  получаем:


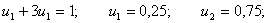
Получаем: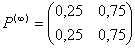 

Матрица переходов 000301

Задана матрица переходов Р1. Найти матрицу Р3.

 

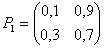
Решение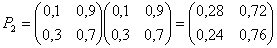

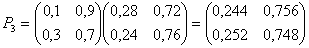
Цепи Маркова 000300

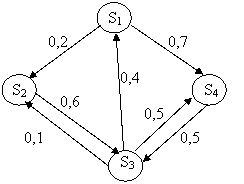
По заданной матрице перехода построить граф состояний.

 

Решение

Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.

Теория массового обслуживания 000299

В ресторан прибывает в среднем 20 посетителей в час. Считая поток посетителей простейшим, и зная, что ресторан открывается в 11.00, определите:
а)  вероятность того, что в 11.12 в ресторан придет 20 посетителей при условии, что в 11.07 их было 18
б) вероятность того, что между 11.28 и 11.30 в ресторане окажется новый посетитель, если известно, что предшествующий посетитель прибыл в 11.25.

Решение

Для ответ на первый вопрос фактически надо найти вероятность того, что в промежуток от 11.07 до 11.12 (τ = 5 минут) придет ровно 2 посетителя. При этом мы знаем интенсивность потока посетителей - λ = 20/60 = 1/3 посетителей в минуту. Конечно, данная величина носит условный характер, т.к. посетители не могут приходить по частям.
Искомая вероятность равна: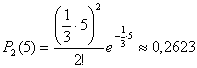

Теперь перейдем ко второму вопросу. Нам не сказано, сколько именно новых посетителей будет в промежутке от 11.28 до 11.30, главное чтобы был хоть один. Эта вероятность равна


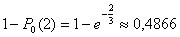
Здесь Р₀ (2) – вероятность того, что в этом промежутке не будет ни одного посетителя

Системы массового обслуживания 000298

В бюро обслуживания в среднем поступает 12 заявок в час. Считая поток заказов простейшим, определить вероятность того, что:
а) за 1 минуту не поступит ни одного заказа,
б) за 10 минут поступит не более трех заказов.
Решение

Сначала найдем плотность (интенсивность) потока, выразив ее в количестве заявок в минуту. Очевидно, эта  величина равна 



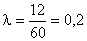
Далее находим вероятность того, что за время  τ = 1 мин не поступит ни одной заявки по формуле:



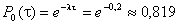
Вероятность того, что за 10 минут поступит не более трех заказов будет складываться из вероятностей того, что не поступит ни одного заказа, поступит один, два или ровно три заказа.

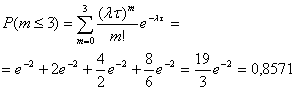Теорема Муавра-Лапласа 000297

Проверкой установлено, что 96% изделий служат не меньше гарантируемого срока. Наугад выбирают 15000 изделий. Найти вероятность того, что со сроком службы менее гарантируемого будет от 570 до 630 изделий.

Решение

Вероятность того, что срок службы изделия будет менее гарантированного равна:

1 – 0,96 = 0,04

Математическое ожидание числа таких изделий равно
 


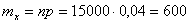
По теореме Муавра - Лапласа получаем:

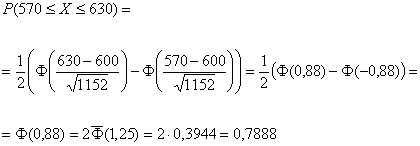
Определить детали 000294

Выборочным путем требуется определить среднюю длину изготавливаемых деталей. Сколько нужно исследовать деталей, чтобы с вероятностью, большей чем 0,9, можно было утверждать, что средняя длина отобранных изделий будет отличаться от  математического ожидания этого среднего (средняя длина деталей всей партии) не более, чем на 0,001 см.? Установлено, что среднее квадратическое отклонение длины детали не превышает 0,04 см.

Решение

По условию если среднее квадратическое отклонение не превышает 0,04, то дисперсия, очевидно, не превышает (0,04)². Также по условию задано, что



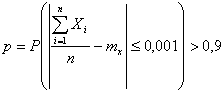
Если преобразовать соотношение, стоящее в скобках и после этого применить неравенство Чебышева, получаем:







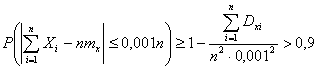
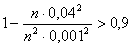
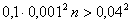
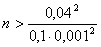
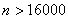
Т.е. для достижения требуемой вероятности необходимо отобрать более 16000 деталей.

Случайные величины 000293

Среднее квадратическое отклонение каждой из 2500 независимых случайных величин не превосходит 3. Оценить вероятность того, что абсолютная величина отклонения среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превосходит 0,3.


Решение

Требуется найти вероятность



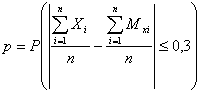
Неравенство Чебышева в случае суммы случайных величин имеет вид:




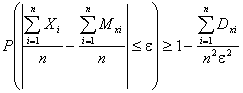
Если среднее квадратическое отклонение не превосходит 3, то, очевидно, дисперсия не превосходит 9. Величина ε по условию задачи равна 0,3.
Тогда


 
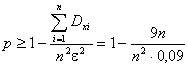
Отсюда получаем

при  n=2500:

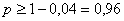Вероятность случайной величины 000292

Суточная потребность электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 3000 кВт/час, а дисперсия составляет 2500. Оценить вероятность того, что в ближайшие сутки расход электроэнергии в этом населенном пункте будет от 2500 до 3500 кВт/час.


Решение

Требуется найти вероятность попадания случайной величины в заданный интервал:



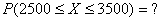
Крайние значения интервала отклоняются от математического ожидания на одну и ту же величину, а именно – на 500. Тогда можно записать с учетом неравенства Чебышева:



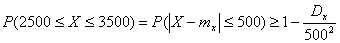
Отсюда получаем:



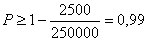
Т.е. искомая вероятность будет не меньше, чем 0,99. 

Величина отклонения 000255

Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,96, можно было ожидать, что абсолютная величина отклонения относительной частоты годных деталей от вероятности детали быть  годной, равной 0,98, не превысит 0,02.

Решение

Условие задачи фактически означает, что выполняется неравенство:



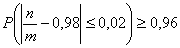
Здесь n- число годных деталей, m- число проверенных деталей. Для применения неравенства Чебышева преобразуем полученное выражение:



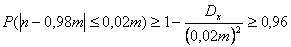
После домножения выражения, стоящего в скобках, на m получаем вероятность отклонения по модулю количества годных деталей от своего математического ожидания, следовательно, можно применить неравенство Чебышева, т.е. эта вероятность должна быть не меньше, чем величина

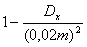
а по условию задачи еще и не меньше, чем 0,96.
Таким образом, получаем неравенство

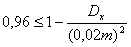
Дисперсия может быть найдена по формуле

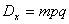
Итого, получаем: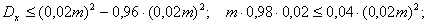 

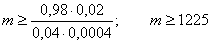
Т.е. для выполнения требуемых условий необходимо не менее 1225 деталей.  

Неравенство Чебышева 000254

Вероятность наступления события А в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что в 10000 испытаниях отклонение относительной частоты появления события А от его вероятности не превзойдет по абсолютной величине 0,01.

Решение

В соответствии с неравенством Чебышева  вероятность того, что отклонение случайной величины от ее математического ожидания будет меньше некоторого числа ε, ограничена в соответствии с неравенством 



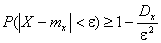
Надо определить математическое ожидание и дисперсию числа появления события А при одном опыте. Для события А случайная величина может принимать одно из двух значений: 1- событие появилось, 0- событие не появилось. При этом вероятность значения 1 равна вероятности р=0,3, а вероятность значения 0- равна вероятности ненаступления события А
q=1 – p =0,7.

По определению математического ожидания имеем:

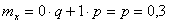
Дисперсия: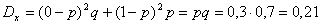 

В случае n независимых испытаний получаем 

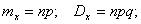
В нашем случае получаем:
 
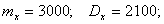
Вероятность отклонения относительной частоты появления события А в п испытаниях от вероятности на величину, не превышающую ε=0,01 равна:

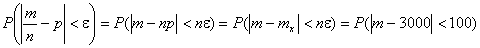
Выражение полученное в результате этих простых преобразований представляет собой не что иное, как вероятность отклонения  числа т появления события А от математического ожидания на величину не большую, чем σ=100.
В соответствии с неравенством Чебышева эта вероятность будет не меньше, чем величина

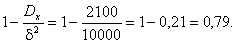
Независимые случайные величины 000253

Задана плотность распределения системы случайных величин Х и Y.



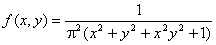
Выяснить являются ли независимыми случайные величины Х и Y.

Решение

Для решения этой задачи преобразуем плотность распределения:



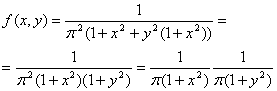
Таким образом, плотность распределения удалось представить в виде произведения двух функций, одна из которых зависит только от х, а другая – только от у. Т.е. случайные величины Х и Y независимы. Разумеется, они также будут и некоррелированы.