| Главная » Статьи » Математика » Теория вероятности |
Случайные величиныСлучайные величины (с.в.) – численное значение появляющееся в результате опыта, и принимающее произвольное значение из заранее определенного множества. Существует два типа случайных величин: дискретные и непрерывные. Дискретные случайные величины принимают в результате испытания одно из изолированного дискретного множества значений. Они хорошо подходят для описания результатов измерений, связанных с подсчетом и выражаемых целыми числами. Примеры дискретных случайных величин: оценка, полученная на экзамене, число попаданий в мишень в серии из 10 выстрелов и т. п. Вероятность принятия дискретной случайной величиной каждого из возможных ее значений больше нуля. Эта вероятность может быть записана как ,P((X = xi)) = Pi где i =... −1, 0, 1 ... Здесь X — обозначение случайной величины; xi— конкретные числовые значения, принимаемые дискретной случайной величиной; pi — вероятности этих значений. Индекс i может в общем случае пробегать значения от −∞ до ∞. Функция P((X = xi)), связывающая значения дискретной случайной величины с их вероятностями, называется ее распределением (законом распределения). Обычно закон распределения записывается в виде таблицы вида
Пример Пусть Х – число очков выпавшее на игральной кости при одном броске. Тогда, эта с.в. распределена по закону
Непрерывные случайные величины в результате испытания могут принимать любые значения из некоторого интервала. Примеры непрерывных случайных величин: спортивный результат в беге или прыжках, рост и масса тела человека, сила мышц и др. Поскольку число возможных значений непрерывной случайной величины бесконечно велико и чаще всего нет оснований предположить, что одни значения появляются существенно чаще других, то вероятность принятия непрерывной случайной величиной каждого отдельного значения оказывается равной нулю. По этой причине нельзя описать распределение непрерывной случайной величины в виде вероятностей ее отдельных значений, как в случае дискретных случайных величин. Здесь необходимы другие подходы, которые рассмотрены в разделах 4.6 и 4.7. Функция распределенияРассмотрим вероятность того, что случайная величина X окажется меньше или равной некоторому заданному числу х, т. е. F(x) = P((X≤ x)) . (4.11) Эта вероятность, рассматриваемая как функция переменной х, называется функцией распределения случайной величины X. Она используется для записи распределений как дискретных, так и непрерывных случайных величин. Функция распределения непрерывной случайной величины будет непрерывной функцией (рис. 4.8). Как было сказано ранее, вероятность принятия непрерывной случайной величиной какого-либо конкретного значения равна 0. Для непрерывной случайной величины обычно интересует вероятность попадания ее в заданный интервал (x1;x2), которая по известной функции распределения находится как P((x1 ≤ X,x2)) = F(x2)F(x1) (4.12) В этом выражении совершенно не обязательно записывать интервал таким образом. Можно было бы записать ,x1<X<x2,x1≤X≤x2 или x1<X ≤ x2 , при этом вероятность попадания случайной величины в интервал не изменится. Это связано с тем, что, как уже отмечалось, функция распределения случайной непрерывной величины не имеет скачков ни при каких значениях х. Свойства функции распределения совпадает со свойствами эмпирической функции распределения (см. 2.3.4) 1. F(x) неубывающая функция. 2. 3. График функция распределения представляет собой теоретический аналог полигона накопленных частот, рассмотренного в разделе 2.3.3.
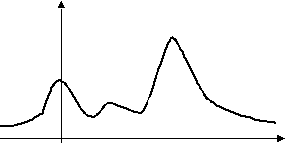
Рис. 4.8. Функция распределения непрерывной случайной величины Плотность распределения вероятностейДля непрерывных случайных величин вводится понятие плотность распределения вероятностей, или "плотность вероятностей”, играющее исключительно важную роль при их описании. Плотность вероятностей — это производная от функции распределения непрерывной случайной величины, т.е. Более подробно при рассмотрении конкретных непрерывных распределений об этой функции рассказано в разделе 4.9. Типичный вид графика плотности вероятностей показан на рис. 4.9. Вероятность попадания непрерывной случайной величины в интервал между значениями х1 и х2 пропорциональная площади под кривой плотности вероятностей, заключенной между точками х1 и х2. Эта вероятность математически записывается в виде интеграла от f(x) в пределах х1 и х2.
Свойства f(x) : 1.f(x) ≥ 0; 2. f(x) = 0 при x < xmin; 3. f(x) = 0 при x > xmin; 4. .
Рис. 4.9. Вид графика плотности распределения вероятностей Числовые характеристики случайных величинРаспределение случайной величины, заданное в виде функции распределения или плотности вероятностей, полностью ее характеризует. Однако такая исчерпывающая характеристика случайной величины сложна и далеко не всегда необходима. Для решения многих практических задач не нужно знать распределение случайной величины, а достаточно иметь лишь некоторые обобщающие числовые характеристики этого распределения. Математическое ожиданиеДля более наглядного определения математического ожидания (среднего значения) случайной величины рассмотрим подход к этому понятию на конкретном примере. Пусть имеется дискретная случайная величина X с
возможными значениями Таким образом, имеем n наблюдений за случайной величиной X,
т. е. выборку объема n. Определим выборочное
среднее арифметическое: Здесь индекс n при Теперь представим, что испытание, состоящее в регистрации количества правонарушений, повторяется неограниченное число раз. Здесь, абстрагируясь от физической реализуемости такого эксперимента, будем считать, что наблюдению доступна вся теоретически бесконечная генеральная совокупность значений случайной величины X. Согласно статистическому определению вероятности, данному в разделе 4.2.2, относительные частоты событий стремятся к их вероятностям при неограниченном повторении испытания. Поэтому в пределе при n→∞
Таким образом, выборочное среднее арифметическое случайной величины X стремится при неограниченном повторении испытания (при неограниченном увеличении объема выборки) к некоторому постоянному числу, так как в последней сумме xi и рi — постоянные числа. Это число носит название математического ожидания (среднего значения) случайной величины. Математическое ожидание обозначает как M(X) или mx. Математическое ожидание дискретной случайной величины равно сумме всех ее возможных значений, умноженных на вероятности этих значений:
(4.16) В этой записи Только что рассмотренный пример показывает, что математическое ожидание — абстрактное понятие. Оно является теоретическим аналогом выборочного среднего арифметического. Математическое ожидание равно среднему значению генеральной совокупности. Для непрерывных случайных величин математическое ожидание определяется с помощью плотности вероятностей по формуле:
(4.17) Свойства математического ожидания1. M(C)=C, 2. M(CX)=CM(X). 3. M(X+Y)= M(X)+M(Y), 4. M(X×Y)= M(X)M(Y), если X и Y – независимые C.B. Дисперсия и стандартное отклонениеТочно так же, как математическое ожидание, являющееся теоретическим аналогом среднего арифметического, можно ввести теоретические аналоги всех числовых характеристик выборки, рассмотренных в гл. 3. Для этого нужно в соответствующих формулах для выборочных характеристик заменить все средние арифметические на математические ожидания. Дисперсией случайной величины X называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания (сравните с определением п. 3.4.2). Дисперсия обозначается как D(Х), или σ². .
Для дискретных случайных величин
(4.18) т. е. дисперсия дискретной случайной величины равна сумме квадратов отклонений отдельных значений случайной величины от ее математического ожидания, умноженных на вероятности этих значений. Для непрерывных случайных величин Положительный корень квадратный из дисперсии называется средним квадратическим (стандартным) отклонением случайной величины. Эта величина обозначается, как σx σx=√D. (4.20) Дисперсия и стандартное отклонение характеризуют изменчивость (вариативность) случайной величины. Чем сильнее случайная величина отклоняется от своего математического ожидания, тем больше величины D(X) и σx . Последнюю (σx) использовать удобнее, так как его размерность совпадает с размерностью случайной величины (например, если Х - кол-во долларов, выигранное в лотерею, то σx - измеряется в $. Свойства дисперсии1. D(C)=0, 2. D(CX)= C2D(X). 3. D(X+Y)= D(X)+D(Y),если X и Y – независимые с.в. Обобщение 4.8.1 и 4.8.2. Пусть Пример Играем в следующую игру: один раз бросаем игральную кость и получаем столько $, сколько выпало очков. Цена игры: 4$. Выгодно ли играть? Пусть с.в. Х – количество очков, выпавшее при броске игральной кости. (см. пример 4.12) Вычислим С.В. Х2 имеет следующее распределение
Вычислив М(Х2)=91/6
находим D(X) = 91/6 – 441/36 = 105/36 = МоментыМатематическое ожидание и дисперсия представляют собой частные случаи общих числовых характеристик случайной величины, называемых моментами. Ниже кратко рассматриваются лишь так называемые центральные моменты случайной величины. S-ым центральным моментом случайной величины X называется математическое ожидание s-й степени отклонения случайной величины от ее математического ожидания: . В частности, при s = 2 второй центральный момент случайной величины есть дисперсия. На практике часто используются также третий и четвертый центральные моменты, позволяющие судить о симметричности и остроте вершины кривой распределения случайной величины. Если μ3 = 0, то распределение симметрично относительно математического ожидания, если μ3>0, то преобладают положительные отклонения от математического ожидания, если μ3<0 — отрицательные. Для удобства применяется так называемый коэффициент асимметрии, который является безразмерной величиной и определяется как Об остроте вершины кривой распределения судят по коэффициенту эксцесса: Если γ4 >0, то распределение имеет острый пик, если γ4<0 (минимальное значение γ4= –2), то распределение имеет плосковершинную форму по сравнению с рассмотренным ниже нормальным распределением, для которого γ4 = 0. | |||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 11584 | | |||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
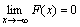
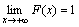
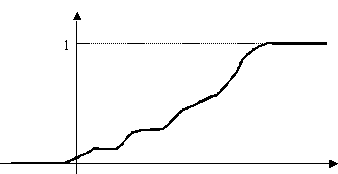
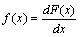 (4.14)
(4.14)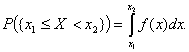 . (4.15)
. (4.15)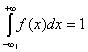
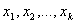 и вероятностями
этих значений
и вероятностями
этих значений 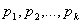 . В качестве
примера X рассмотрим случайную величину — количество
правонарушений за сутки. Каждое из значений
. В качестве
примера X рассмотрим случайную величину — количество
правонарушений за сутки. Каждое из значений 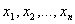 (отмечено 0;
1; ... нарушений) будет наблюдаться некоторое число раз. Обозначим эти числа
через
(отмечено 0;
1; ... нарушений) будет наблюдаться некоторое число раз. Обозначим эти числа
через 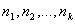 . Очевидно, что
сумма
. Очевидно, что
сумма 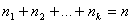 .
.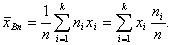
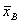 обозначает,
что среднее арифметическое вычислено по n наблюдениям.
обозначает,
что среднее арифметическое вычислено по n наблюдениям.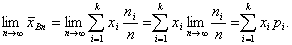
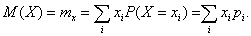
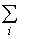 означает, что
суммирование производится по всем возможным i.
означает, что
суммирование производится по всем возможным i.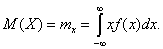
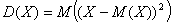
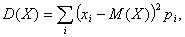
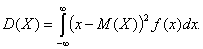
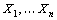 – с.в., а
– с.в., а 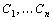 – константы.
Тогда
– константы.
Тогда 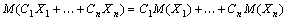 . В частности
. В частности 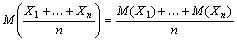 . Если более
того
. Если более
того 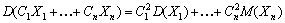
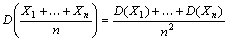
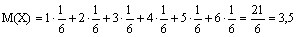 – именно столько очков
(а, значит, и $) ”в среднем” мы будем получать если играть достаточно долго.
Значит, игра невыгодна для нас. Мы ”в среднем” теряем 0.5$ в каждой
игре.
– именно столько очков
(а, значит, и $) ”в среднем” мы будем получать если играть достаточно долго.
Значит, игра невыгодна для нас. Мы ”в среднем” теряем 0.5$ в каждой
игре. 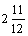 .
.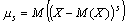
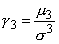 (4.21)
(4.21)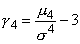 (4.22)
(4.22)