| Главная » Статьи » Математика » Геометрия |
Формулы треугольника
Стороны треугольника связаны следующими неравенствамиa ≤ b + cb ≤ a + c
c ≤ a + b
В случае выполнения равенства в одном из них треугольник называется вырожденным. Далее везде предполагается невырожденный случай. Треугольник можно однозначно (с точностью до сдвига и поворота) определить по следующим тройкам основных элементов: a, b, c — по трем сторонам;a, b, C
— по двум сторонам и углу между ними;a, B, C
— по стороне и двум прилежащим к ней углам.Сумма углов любого треугольника постоянна A + B + C = 180°
1. Прямоугольный треугольник. Определение тригонометрических функций.Рассмотрим прямоугольный треугольник, показанный на рисунке.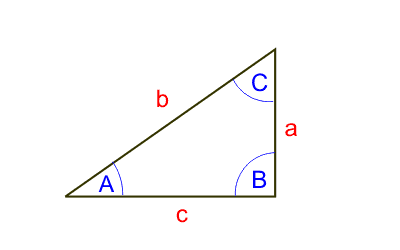 Функция синус: sin(A) = a/b.Функция косинус: cos(A) = c/b.Функция тангенс: tg(A) = a/c.Функция котангенс: ctg(A) = c/a.2. Прямоугольный треугольник. Тригонометрические формулы.a = b * sin(A)c = b * cos(A)
a = c * tg(A)
3. Прямоугольный треугольник. Теорема Пифагора.b2 = a2 + c2С помощью теоремы Пифагора можно построить прямой угол, если под рукой нет подходящих инструментов, например, угольника. С помощью двух линеек или двух кусков веревки отмеряем катеты длиной 3 и 4. Потом сдвигаем или раздвигаем их, пока длина гипотенузы не станет равной 5 (32 + 42 = 52). 4. Теорема синусовa/sin(A) = b/sin(B) = c/sin(C) = 2*R5. Теорема косинусовCos(A) = (b2+c2-a2)/(2*b*c)6. Формула расчета площади треугольника (1)S = b*c*sin(A)/27. Формула расчета площади треугольника (2). Формула ГеронаS = (p * (p-a) * (p-b) * (p-c))1/28. Формула расчета площади треугольника (3)S = p * (p-a) * tg (A/2)9. Формула расчета радиуса описанной окружности (1)R = a/(2*sin(A))10. Формула расчета радиуса описанной окружности (2)R= a*b*c /(4*S )11. Формула расчета радиуса вписанной окружности (1)R = S/p12. Формула расчета радиуса вписанной окружности (2)R = (p-a)*tg(A/2) | |
| Просмотров: 6271 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта