| Главная » Статьи » Математика » Геометрия |
Математические софизмы
Софизм- это умышленное ложное умозаключение, которое имеет видимость правильного. Он обязательно содержит одну или несколько замаскированных ошибок. В математических софизмах часто выполняются "запрещенные" действия, не учитываются условия применимости формул и правил1. Я выбрал эту тему для своего реферата потому что она меня заинтересовала. Мне было интересно узнать, что некоторые заведомо ложные утверждения, оказывается, можно доказать. В процессе работы над рефератом я выяснил, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой, так и то, что прямой угол равен тупому. Эта тема сейчас актуальна, потому что софизм- это обман, а так как не каждый может его распознать, то с помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия назад. ^ Цель моего исследования – узнать что такое математические софизмы и научиться их решать. В задачи реферата входит: узнать, как они появились научиться распознавать софизмы научиться их доказывать рассмотреть софизмы в общем рассмотреть арифметические софизмы рассмотреть алгебраические софизмы рассмотреть геометрические софизмы В своем реферате я использовал разные сборники софизмов, таких как «Софизмы. Алгебра. Геометрия. Тригонометрия» Т.Н. Михеевой и учебное пособие А.А. Афанасьевой « История философской мысли». ^ Глава №1.Что такое софизмы. В этой главе рассказывается история софизмов в целом и математических софизмов в частности. §1.История термина «софизм» Софизмы – это умышленные ложные умозаключения, которые имеют вид правильных. Они обязательно содержат одну или несколько замаскированных логических ошибок. Например, в математических софизмах часто выполняются «запрещенные» действия, такие как деление на ноль, не учитываются условия применимости формул и правил. Софистика – направление философии, которое возникло в V-IV вв. до н.э. в Греции и стало очень популярным а Афинах. Софистами называли платных «учителей мудрости», которые учили граждан риторике, искусству слова, приемам ведения спора, красноречию. Одним из представителей софистов был философ Протагор, который говорил: «Я обучаю людей риторике, а это и есть гражданское искусство». Софисты считали, что истина субъективна, то есть у каждого человека своя истина, человек сам создает себе истину и сам же её оценивает, поэтому в суждениях об истине очень много личного. Справедливость, как и истина, у каждого человека тоже своя, а значит, о каждой вещи можно судить двояко, то есть о каждой вещи есть два противоположных мнения. Софисты учили людей оценивать одно и то же событие, как положительное и как отрицательное одновременно, таким образом они приучали людей к широте взглядов2. Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении. Софисты в своих рассуждениях использовали разные ошибки, такие как: логические и ошибки в рассуждениях. Например: «Закон Моисеев запрещал воровство, закон Моисеев потерял свою силу, следовательно, воровство не запрещено», «Все люди разумные существа, жители планет не люди, следовательно, они не разумные существа; терминологические – неправильное употребление слов или построение предложения. Например «Все углы треугольника = π» в смысле «Сумма углов треугольника = π», «сколько пять плюс два умножить на два?» Здесь трудно решить имеется ли в виду 9 (т.е. 5 + (2*2)) или 14 (т.е. (5 + 2) * 2); ошибки в применении формул. Например : Чётное и нечётное. 5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные! ^ §2 Математические софизмы. Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Поиск ошибки в софизме ведет к ее пониманию и осознанию, а осознавая ошибку, человек имеет больше шансов ее не допустить. Также, в истории развития математики софизмы способствовали повышению точности формулировок и более глубокому пониманию понятий математики. Математические софизмы делятся на арифметические, алгебраические и геометрические. ^ Глава №2. Арифметические и алгебраические софизмы. В данной главе я рассмотрю алгебраические и арифметические софизмы, и решу некоторые из них. ^ §3 Арифметические софизмы. Арифметические софизмы– это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. Дважды два – пять. Доказательство: Пусть исходное соотношение - очевидное равенство: 4:4= 5:5 (1) . Вынесем за скобки общий множитель каждой чести (1) равенства, и мы получим: 4*(1:1)=5*(1:1) (2) Разложим число 4 на произведение 2 *2 (2*2)* (1:1)=5*(1:1) (3) Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5. Ошибка: Ошибка заключается в том, что нельзя было выносить множитель за скобки в уравнение №2. ^ Один рубль не равен ста копейкам. Доказательство: Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd. Применим это положение к двум очевидным равенствам 1 р.=100 коп, (1) 10р.=10*100коп.(2) Перемножая эти равенства почленно, получим 10 р.=100000 коп. Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп. таким образом, один рубль не равен ста копейкам. Ошибка: Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями. ^ Число, равное другому числу, одновременно и больше, и меньше его. Доказательство: Возьмем два положительных равных числа a и b и напишем для них следующие неравенства: a > - b b > - b. Перемножив оба этих неравенства почленно, получим неравенство a·b>b·b, Разделим его на b (это законно, т.к. b>0), получим a > b. Записав же два других столь же бесспорных неравенства: b > - a a > - a Перемножив оба этих неравенства почленно, получим неравенство b·a > a·a. Разделив на a>0, придем к b > a. Итак, число a, равное числу b, одновременно и больше, и меньше его. Ошибка: Ошибка заключается в неправильном почленном перемножении, вследствие которого место выражений a>-b ; b>-a получились выражения a>b; a ^ Единица равна нулю. Доказательство: Возьмем уравнение x-a=0 Разделив обе его части на х-а, получим х-а/х-а=0/х-а Откуда сразу же получаем требуемое равенство 1=0 Ошибка: Ошибка в том, что х-а равно нуля а на ноль делить нельзя ^ §4 Алгебраические софизмы. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях. Все числа равны между собой. Доказательство: Возьмем любые два числа х,у. Рассмотрим тождество х2 – 2ху +у2 =у2 – 2ху +х2 Имеем (х - у)2 = (у – х)2 Отсюда х-у = у-х или 2х= 2у, а, значит, х = у. Ошибка: Ошибка заключается в том, что из равенства (х - у)2 = (у – х)2 следует, что , а это равенство справедливо для любых чисел у, х. ^ Единица равна нулю Доказательство: Возьмем уравнение x-a=0 Разделив обе его части на х-а, получим х-а/х-а=0/х-а Откуда сразу же получаем требуемое равенство 1=0 Ошибка: Здесь используется распространенная ошибка, а именно деление на 0. Всякое число равно своему удвоенному значению Доказательство: Запишем очевидное для любого числа а тождество 2а-2а= 2а-2а. Вынесем а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получив: а(а-а)=(а+а)(а-а) (1) Разделив обе части на а-а, получим а=а+а а=2а Ошибка: Ту опять же используется деление на нуль неравенства (1) (а-а=0 ). ^ Если одно число больше другого, то эти числа равны Доказательство: Возьмем два произвольных числа Х и У , такие, что Х > У , и другие три произвольных числа а, b и с , сумма которых равна d , т.е. а+ b + c = d . Умножив обе части этого равенства на Х , а затем на У , получим: Хa+Хb+Хc=Хd, Уa+Уb+Уc=Уd Сложив почленно эти равенства получим Хa + Хb + Хc + Уd = Уa + Уc + Уb + Хd . Перенося здесь Уd вправо , а Хd влево, имеем Хa+Хb+ХcХd=Уa+Уb+УcУd Вынося слева число Х , а справа число У за скобки, придем к соотношению m(a+b+cd)=n(a+b+cd) , (1) Разделив обе части последнего равенства на ( a + b + c d ) , находим, что. У=Х Ошибка: Ошибка, как и в предыдущих примерах заключается в делении на 0, то есть на ( a + b + c d ) ^ Глава №3. Геометрические и логические софизмы. В этой главе я рассмотрю логические и геометрические софизмы, и решу некоторые из них. §5 Геометрические софизмы. Геометрические софизмы основаны на ошибках связанных с геометрическими фигурами и действиями над ними. ^ Спичка вдвое длиннее телеграфного столба. Доказательство: Пусть а длина спички и b дм - длина столба. Разность между b и a обозначим через c . Имеем b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b2 - ab = ca + c2. Вычтем из обеих частей bc. Получим: b2- ab - bc = ca + c2 - bc, или b(b - a - c) = - c(b - a - c), откуда b = - c, но c = b - a, поэтому b = a - b, или a = 2b. Ошибка: Ошибка заключается в том, что в выражении b(b-a-c )= -c(b-a-c) производится деление на 0 ^ Хорда, не проходящая через центр окружности, равна диаметру. Доказательство: 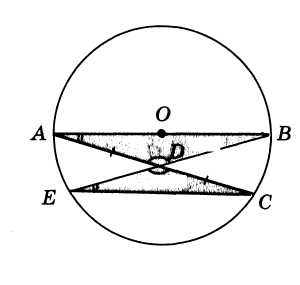 Пусть в окружности приведен диаметр АВ. Через точку В проведем любую хорду ВЕ, не проходящую через центр, затем через середину этой хорды D и точку А проведем новую хорду АС. Наконец, точки Е и С соединим отрезком прямой. Рассмотрим ∆ АВD и ∆ЕDС. В этих треугольниках: ВD = DЕ (по построению), А= Е (как вписанные, опирающиеся на одну и ту же дугу). Кроме того, ВDА= ЕDC (как вертикальные). Если же сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны. Значит, ∆ ВDА= ∆ЕDC , а в равных треугольниках против равных углов лежат равные стороны. Поэтому, АВ=ЕС. По теореме о признаке равенства треугольника: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. А в нашем случае, А не прилежит к стороне В D . Ошибка: Ошибка заключается в неправильном применении теоремы о равенстве треугольников.(равны 2 угла , не прилежащие к одной стороне). ^ §6 Логические софизмы. Логические софизмы- софизмы, ошибки которых заключаются в неправильных рассуждениях. Полупустое и полуполное Доказательство: Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное Ошибка: Полупустое не является половиной чего либо пустого, а является чем либо наполовину наполненным. Вор Доказательство: Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего. Заключение. Можно бесконечно говорить о софизмах в целом и о математических софизмах в частном. Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы - это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений. Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. Существует огромное множество разных видов софизмов. И математические софизмы – всего лишь небольшая их часть. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм. Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться и всматриваться, например в софизме «Хорда, не проходящая через центр окружности, равна диаметру» пришлось долго искать ошибку в применении теоремы. К концу работы над рефератом ошибки стали находиться быстрее. Хорошо развитое логическое мышление может помочь не только в решении задач, но и в обычной жизни. Вообще, решение софизмов – интересное и познавательное занятие. Им можно заниматься как целенаправленно, так и в свободное время для собственного удовольствия, как например решение сканвордов или судоку. | |
| Просмотров: 10301 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта