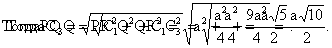| Главная » Статьи » Математика » Геометрия |
ПОСТРОЕНИЯ НА ИЗОБРАЖЕНИЯХ ПЛОСКИХ ФИГУР(2)
4.3. Расстояние между скрещивающимися прямыми.Для нахождения расстояния между скрещивающимися прямыми а и b можно использовать следующий план:1. На одной из данных прямых, например на прямой b, выбираем некоторую точку W и строим плоскость α, определяемую прямой α и точкой W. 2. В плоскости α через точку W проводим прямую а1а║а. 3. Строим плоскость β, определяемую пересекающимися прямыми а1 и b. Ясно, что так как прямая α параллельна прямой а1 , то прямая α параллельна и плоскости β. Поэтому точки прямой а одинаково удалены от плоскости β. Расстояние от любой точки U прямой а до плоскости β равно расстоянию между скрещивающимися прямыми а и b. Таким образом, задача нахождения расстояния между скрещивающимися прямыми может быть сведена к задаче нахождения расстояния от точки до плоскости. Задача 11. В основании пирамиды МАВС лежит равнобедренный треугольник с прямым углом при вершине С. Высота пирамиды проектируется в точку О – середину ребра АВ, и угол АМВ=900. На ребре МА взята P – середина этого ребра, а грани МВС взята точка Q, в которой пересекаются медианы грани МВС. Найти расстояние между прямыми АВ и PQ, если ВС=а. Решение (рис. 26). Выполним дополнительные построения в соответствии с рекомендуемым выше планом. 1. 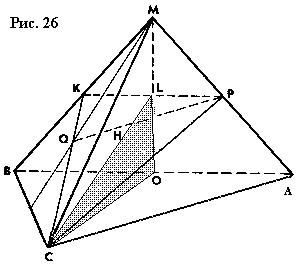 Через прямую АВ и точку P, лежащую на другой заданной прямой, уже проведена плоскость α – это плоскость МАВ. 2. В плоскости МАВ через точку Р проведем прямую РК║АВ. 3. Строим плоскость β, определяемую прямыми PQ и РК. Ясно, что так как точка Q – точка пересечения медиан треугольника МВС, то прямая KQ пройдет через вершину С. Таким образом, в сечении пирамиды плоскостью β получаем треугольник СКР. Так как прямая АВ║РК, то прямая АВ параллельна плоскости СКР. Найдем расстояние, например, от точки О –середины ребра АВ до плоскости СКР. Для этого через точку О проведем плоскость γ , перпендикулярную какой-нибудь прямой. Лежащей в плоскости СКР, например, прямой РК. Так как прямая РК║АВ, то плоскость γ будет тогда перпендикулярна и прямой АВ. Итак, в плоскости МАВ прямая ОМ перпендикулярна прямой АВ, и, легко убедиться, в плоскости АВС прямая ОС перпендикулярна прямой АВ. Тогда плоскость, определяемая пересекающимися прямыми ОМ и ОС, - это и есть плоскость γ перпендикулярная прямой АВ, т. е. и прямой РК. Через прямую АВ и точку P, лежащую на другой заданной прямой, уже проведена плоскость α – это плоскость МАВ. 2. В плоскости МАВ через точку Р проведем прямую РК║АВ. 3. Строим плоскость β, определяемую прямыми PQ и РК. Ясно, что так как точка Q – точка пересечения медиан треугольника МВС, то прямая KQ пройдет через вершину С. Таким образом, в сечении пирамиды плоскостью β получаем треугольник СКР. Так как прямая АВ║РК, то прямая АВ параллельна плоскости СКР. Найдем расстояние, например, от точки О –середины ребра АВ до плоскости СКР. Для этого через точку О проведем плоскость γ , перпендикулярную какой-нибудь прямой. Лежащей в плоскости СКР, например, прямой РК. Так как прямая РК║АВ, то плоскость γ будет тогда перпендикулярна и прямой АВ. Итак, в плоскости МАВ прямая ОМ перпендикулярна прямой АВ, и, легко убедиться, в плоскости АВС прямая ОС перпендикулярна прямой АВ. Тогда плоскость, определяемая пересекающимися прямыми ОМ и ОС, - это и есть плоскость γ перпендикулярная прямой АВ, т. е. и прямой РК.
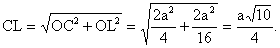 Таким образом, искомое расстояние ОН. Таким образом, искомое расстояние ОН. | ||||
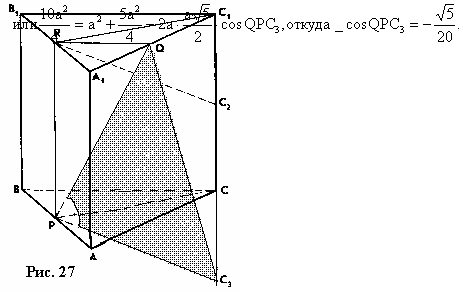 Итак, в треугольнике PQС3 известны все стороны. Далее С3 Q²= =С3P²+PQ²-2 С3P·PQ cos QPC3, Таким образом, угол QPC3 тупой, поэтому искомый угол φ=180º- QPC3, и, значит, cos φ =cos(180º- QPC 3)= - сos QPC3.
Итак, в треугольнике PQС3 известны все стороны. Далее С3 Q²= =С3P²+PQ²-2 С3P·PQ cos QPC3, Таким образом, угол QPC3 тупой, поэтому искомый угол φ=180º- QPC3, и, значит, cos φ =cos(180º- QPC 3)= - сos QPC3. 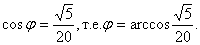 4.5. Угол между прямой и плоскостью.
4.5. Угол между прямой и плоскостью.
При решении задач этого типа применяется либо поэтапно-вычислительный метод, либо геометрический. Пусть в задаче требуется найти угол φ между прямой АВ и плоскостью α. При решении задачи поэтапно-вычислительным методом необходимо сначала построить проекцию прямой АВ на плоскость α. Для этого следует из какой-нибудь точки прямой АВ опустить перпендикуляр на плоскость α. Затем необходимо подсчитать какие-нибудь две стороны полученного треугольника, в который входит угол φ, и найти какую-либо тригонометрическую функцию угла φ, а потом и сам угол. Задача 13. В правильной призме ABCA1B1C1 угол между прямыми АB1 и A1С равен 2α. Найти угол между прямой BC1 и плоскостью AСC1. Решение (рис. 28). Выполним дополнительные построения. В плоскости ABB1 через точку A1 проведем прямую, параллельную прямой B1А, и точку пересечения построенной прямой с прямой ВА обозначим D. Тогда угол DA 1C=2α. Соединим точку D с точкой С и проведем в треугольнике A1 CD медиану A1К. Так как заданная призма – правильная, то ее боковые грани – равные прямоугольники, и, следовательно, B1А=A1C. Кроме того, B1А=A1D. Тогда и A1D=A1 C, т. е. в треугольнике A1CD A1К┴СD. Проведем далее в равностороннем треугольнике АВС медиану ВМ. Тогда ВМ┴АС. Но ясно и то, что прямая A1А перпендикулярна плоскости АВС, т. е. A1 А┴ВМ, или, наоборот, ВМ ┴ A1А. Так как прямая ВМ перпендикулярна двум пересекающимся прямым плоскости AСС1, и, значит, соединив точку М с точкой С1, получим прямую С1М – проекцию прямой ВС1 на плоскость AСС1 и прямоугольный треугольник С1ВМ, угол ВС1М которого является углом между прямой ВС1 и плоскостью АСС1. 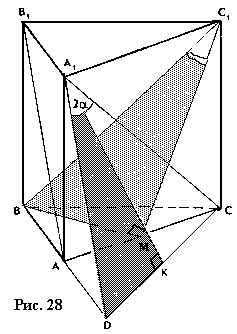 Рассмотрим прямоугольные треугольники С1ВМ и А1DK. У них С 1В=А1D, и так как в треугольнике АCD CD=АС√3, то DK=½АС√3. Но и а треугольнике АВС ВМ=½АС√3. Таким образом, ВМ=DK. Итак, прямоугольные треугольники С1ВМ и А1 DK равны (по гипотенузе и катету). Тогда углы ВС1М и DА1K равны. Но ясно, что угол DА1K=α. Следовательно, и угол ВС1 М=α.
Рассмотрим прямоугольные треугольники С1ВМ и А1DK. У них С 1В=А1D, и так как в треугольнике АCD CD=АС√3, то DK=½АС√3. Но и а треугольнике АВС ВМ=½АС√3. Таким образом, ВМ=DK. Итак, прямоугольные треугольники С1ВМ и А1 DK равны (по гипотенузе и катету). Тогда углы ВС1М и DА1K равны. Но ясно, что угол DА1K=α. Следовательно, и угол ВС1 М=α.4.6. Угол между плоскостями.
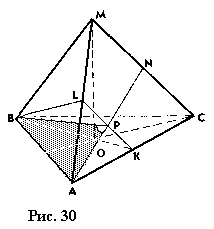
Пусть П1 и П2 – данные плоскости, пересекающиеся по прямой АВ (рис. 29). Через некоторую точку F прямой АВ проведем в плоскости П1 прямую FC^AB, а в плоскости П2 прямую FD^AB. Плоскость CFD, таким образом, перпендикулярна прямой АВ, и угол j между прямыми FC и FD является углом между плоскостями П1 и П2 . По определению угла между прямыми 0°<j£90°. Одним из методов решения задач на нахождение угла между плоскостями является поэтапно-вычислительный метод. Применение этого метода может опираться на использование формулы. На ребрах АС и МА правильного тетраэдра МАВС взяты соответственно точки К и L – середины этих ребер. Найти угол между плоскостями BLK и МАС. Решение (рис. 30). Построим угол между плоскостями BLK и МАС. Для построения перпендикуляра из точки В на прямую LK – линию пересечения плоскостей BLK и МАС воспользуемся тем, что в треугольнике BLK BL=BK (как медианы равносторонних треугольников). Тогда медиана ВР является перпендикуляром к стороне LK. Так как в треугольнике ALK AL=AK, то медиана АР перпендикулярна стороне LK. Таким образом, угол между прямыми ВР и АР – угол между плоскостями BLK и МАС. Пусть прямая АР пересекает ребро МС в точке N. Найдем угол ВРА треугольника ВРА. Полагая для выполнения подсчетов ребро тетраэдра равным а, получаем  Из прямоугольного треугольника ВРК, в котором
Из прямоугольного треугольника ВРК, в котором 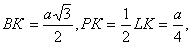 находим, что
находим, что 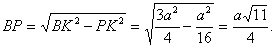 Теперь в треугольнике ВРА известны все стороны. По теореме косинусов получаем
Теперь в треугольнике ВРА известны все стороны. По теореме косинусов получаем 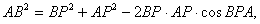 или
или
 Из прямоугольного треугольника ВРК, в котором
Из прямоугольного треугольника ВРК, в котором 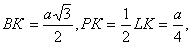 находим, что
находим, что 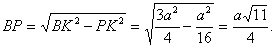 Теперь в треугольнике ВРА известны все стороны. По теореме косинусов получаем
Теперь в треугольнике ВРА известны все стороны. По теореме косинусов получаем 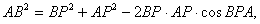 или
или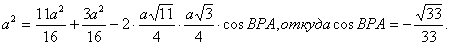
 Так как cos BPA<0. то ÐВРА – тупой. Таким образом, углом между прямыми ВР и АР является угол j=180°-ÐВРА. Тогда cos j=cos (180° -ÐВРА)=--cos BPA=
Так как cos BPA<0. то ÐВРА – тупой. Таким образом, углом между прямыми ВР и АР является угол j=180°-ÐВРА. Тогда cos j=cos (180° -ÐВРА)=--cos BPA=  Итак, угол между плоскостями BLK и МАС – j=arccos
Итак, угол между плоскостями BLK и МАС – j=arccos 
4.7. Двугранный и многогранный углы.
Если j - величина двугранного угла, то 0°<j<180°. При решении задач на нахождение двугранного угла могут быть применены геометрический, а также поэтапно-вычислительный методы. Применение поэтапно-вычислительного метода связано необходимость построения линейного угла искомого двугранного угла j и с построением треугольника, содержащего этот угол j или угол j1 =180°-j.Подсчитывая стороны построенного треугольника, находят угол j.Задача 15.
В основании пирамиды МАВС лежит прямоугольный треугольник. Боковое ребро МВ перпендикулярно плоскости основания, и АС=ВС. На ребре МС взята точка К – середина этого ребра. Найти двугранный угол ВКАС, если: а)МВ=АС; б)МВ=2АС. Решение а) (рис. 31, а).
Геометрический метод. Так как прямая МВ перпендикулярна плоскости АВС, то МВ^АС, т. е. И АС^МВ. Таким образом, АС^ВС и АС^МВ, следовательно, АС^ВК, т. е. и ВК^АС (1). Так как в треугольнике МВС МВ=ВС, то ВК не только медиана этого треугольника, но и ВК^МС (2). Из результатов (1) и (2) следует, что прямая ВК перпендикулярна плоскости МАС. Тогда плоскость АВК, проходящая через прямую ВК, также перпендикулярна плоскости МАС. Другими словами, двугранный угол ВАКС равен 90°. б) (рис. 31, б)
Поэтапно-вычислительный метод. Построим линейный угол искомого двугранного угла, ребром которого является прямая АК, а гранями – полуплоскости ВАК и САК.
1. В треугольнике АСК через вершину С проведем прямую, перпендикулярную ребру АК искомого двугранного угла. Подсчитаем для этого все стороны треугольника АСК, полагая, например, АС=а. Тогда ВС=а, МВ=2а , МС=аÖ5, СК=½СМ=½Ö5, АК2=АС2 +СК2, т. е. АК= .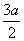
 Если СН^АК, то СН·АК=АС·СК, откуда СН=
Если СН^АК, то СН·АК=АС·СК, откуда СН= 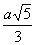 . Тогда АН=
. Тогда АН=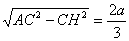 , и, следовательно, АН:АК=4:9, откуда ясно построение точки Н и затем прямой СН, которая перпендикулярна прямой АК.
, и, следовательно, АН:АК=4:9, откуда ясно построение точки Н и затем прямой СН, которая перпендикулярна прямой АК.
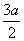
 Если СН^АК, то СН·АК=АС·СК, откуда СН=
Если СН^АК, то СН·АК=АС·СК, откуда СН= 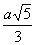 . Тогда АН=
. Тогда АН=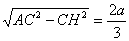 , и, следовательно, АН:АК=4:9, откуда ясно построение точки Н и затем прямой СН, которая перпендикулярна прямой АК.
, и, следовательно, АН:АК=4:9, откуда ясно построение точки Н и затем прямой СН, которая перпендикулярна прямой АК. 2. В треугольнике АВК через вершину В проведем прямую, перпендикулярную ребру АК двугранного угла ВАКС. Для этого подсчитаем стороны треугольника АВК. Получаем АВ=аÖ2, ВК=½МС=½а√2 и АК= 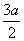 . Если BF^АК, АВ2-AF2=ВК2-KF2, или 2 а2-AF2=
. Если BF^АК, АВ2-AF2=ВК2-KF2, или 2 а2-AF2= 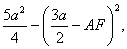 откуда AF=а, и, следовательно, AF:АК=2:3. Таким образом, ясно построение точки F и затем прямой BF, которая перпендикулярна прямой АК.
откуда AF=а, и, следовательно, AF:АК=2:3. Таким образом, ясно построение точки F и затем прямой BF, которая перпендикулярна прямой АК.
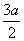 . Если BF^АК, АВ2-AF2=ВК2-KF2, или 2 а2-AF2=
. Если BF^АК, АВ2-AF2=ВК2-KF2, или 2 а2-AF2= 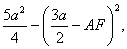 откуда AF=а, и, следовательно, AF:АК=2:3. Таким образом, ясно построение точки F и затем прямой BF, которая перпендикулярна прямой АК.
откуда AF=а, и, следовательно, AF:АК=2:3. Таким образом, ясно построение точки F и затем прямой BF, которая перпендикулярна прямой АК. 3. В треугольнике АСК через точку F проведем прямую FL║СН. Тогда FL^АК. Так как, кроме того, BF^АК, то ÐBFL – линейный угол двугранного угла ВАКС.
4. Соединим точку В с точкой L и подсчитаем стороны треугольника BFL. BF= 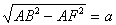 . Из подобия треугольников AFL и АСН следует, что FL:CH=AF:AH, где AF=a, АН=
. Из подобия треугольников AFL и АСН следует, что FL:CH=AF:AH, где AF=a, АН= 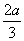 , СН=
, СН=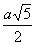 . Тогда FL=
. Тогда FL=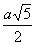 . Так как AL=
. Так как AL=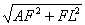 =
=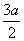 , то CL=AL – AC=½a. Тогда BL=
, то CL=AL – AC=½a. Тогда BL= 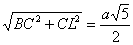 . Итак, в треугольнике BFL известны все стороны: BF=a, FL=
. Итак, в треугольнике BFL известны все стороны: BF=a, FL= 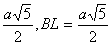 . 5. Из треугольника BFL по теореме косинусов получаем: BL2=BF2+FL2-2BF·FL·cosBFL, или
. 5. Из треугольника BFL по теореме косинусов получаем: BL2=BF2+FL2-2BF·FL·cosBFL, или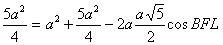 , откуда cosBFL=
, откуда cosBFL= 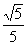 . Это значит, что двугранный угол ВАКС равен arccos.
. Это значит, что двугранный угол ВАКС равен arccos.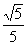
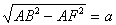 . Из подобия треугольников AFL и АСН следует, что FL:CH=AF:AH, где AF=a, АН=
. Из подобия треугольников AFL и АСН следует, что FL:CH=AF:AH, где AF=a, АН= 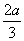 , СН=
, СН=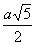 . Тогда FL=
. Тогда FL=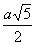 . Так как AL=
. Так как AL=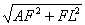 =
=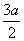 , то CL=AL – AC=½a. Тогда BL=
, то CL=AL – AC=½a. Тогда BL= 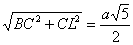 . Итак, в треугольнике BFL известны все стороны: BF=a, FL=
. Итак, в треугольнике BFL известны все стороны: BF=a, FL= 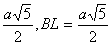 . 5. Из треугольника BFL по теореме косинусов получаем: BL2=BF2+FL2-2BF·FL·cosBFL, или
. 5. Из треугольника BFL по теореме косинусов получаем: BL2=BF2+FL2-2BF·FL·cosBFL, или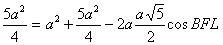 , откуда cosBFL=
, откуда cosBFL= 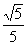 . Это значит, что двугранный угол ВАКС равен arccos.
. Это значит, что двугранный угол ВАКС равен arccos.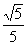
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта
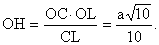
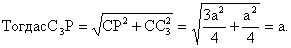 В прямоугольном треугольнике PСC3 СР=½ а√3, СC3=С1С2=½ а. В прямоугольном треугольнике QС1С3 С1Q=½ а, С1С3=½ 3а.
В прямоугольном треугольнике PСC3 СР=½ а√3, СC3=С1С2=½ а. В прямоугольном треугольнике QС1С3 С1Q=½ а, С1С3=½ 3а.