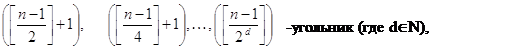| Главная » Статьи » Математика » Геометрия |
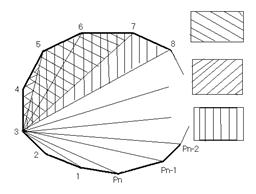
Выпуклый многоугольник с n сторонами можно разбить на треугольники диагоналями, Определение: назовем правильным разбиением выпуклого n-угольника на треугольники
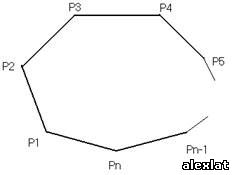
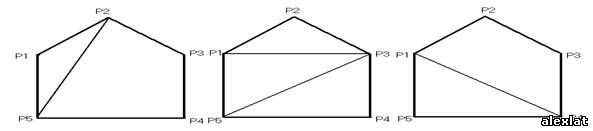
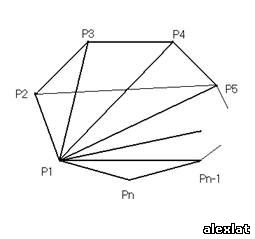
Пусть P1, Пусть i=2 – одна группа правильных разбиений, которая всегда содержит диагональ P2Pn .Число разбиений, входящих в эту группу совпадает с числом правильных разбиений (n-1) угольника P2P3…Pn, то Пусть i=3 – одна группа правильных разбиений, которая всегда содержит диагональ P3P1 и P3Pn.Следовательно, число правильных разбиений, входящих в эту группу, совпадает с числом При i=4 среди треугольников разбиение непременно содержит треугольник P1P4Pn.К нему Аn-3.Следовательно, полное число правильных разбиений, содержащихся в этой группе, равно Аn-3A4.Группы с i=4,5,6,… содержат Аn-4A5, При i=n-2 число правильных разбиений в группе совпадает с числом правильных разбиений в группе с i=2,то есть равно Аn-1. Поскольку А1=А2=0, А3=1, A4=2 и т.к. n ³ 3, то число правильных разбиений равно: Аn= Аn-1+Аn-2+Аn-3 A4+Аn-4 A5+ … + A 5Аn-4+ A4Аn-3+ Аn-2+ Аn-1. Например: A 5= A4+
A6= A5+ А4+ А4+ A5=14 A7= A6+ А5+ А4 *А4+А5+ A6 =42 A8= A7+ А6+А5*А4+ А4*А5+А6+ A7 =132 П.2.1. Найдем количество во всех диагоналей правильных разбиениях, которые пересекают внутри только одну диагональ. Проверяя на частных случаях, пришли к предположению, что количество диагоналей в выпуклых n-угольниках Докажем предположение, что P1n= Аn(n-3)
Каждый n-угольник можно разбить на (n-2) треугольника, из которых можно сложить (n-3) четырехугольника, причем каждый четырехугольник будет иметь диагональ. Но в четырехугольнике можно провести 2 диагонали, значит в (n-3) четырехугольниках можно провести (n-3) дополнительные диагонали. Значит, в П.2.2. Найдем количество во всех диагоналей правильных всех разбиениях, которые пересекают внутри только две диагонали. Проверяя на частных случаях, пришли к предположению, что количество диагоналей в выпуклых n-угольниках Докажем предположение, что P2n=(n-4)Аn , где n ≥ 5.
n-угольник можно разбить на (n-2) треугольников из которых можно сложить П.2.3. Разбиение n-угольника, в котором дополнительные диагонали пересекают главные k Определение 1:Главными диагоналями выпуклого n-угольника называются диагонали, которые Замечание: их существует (n-3). Определение 2:Дополнительными диагоналями выпуклого n-угольника называются диагонали, Замечание: их существует менее (n-3). I.Определение k:
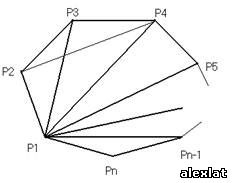
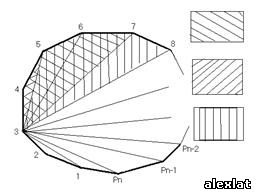
Будем выделять из выпуклого n-угольника 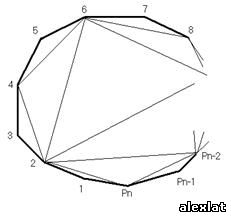 следующим образом: соединяем диагоналями через одну вершину данного n-угольника, причем Итак, за 1 цикл 2 пересечения, за 2 цикла – 4, за 3 – 6, очевидна арифметическая прогрессия с разностью 2, a1=2 и количество членов равным d; значит k=2+2(d-1)=2d – только в том случае, если конечной фигурой окажется треугольник. В противном случае k=2d+1, так как четырехугольник имеет собственную диагональ. Рассчитаем d: т.к.: d=1, n Є [22+1; 23] d=2, nЄ [23+1; 24] d=3, nЄ [24+1; 25] … Зависимость d от n- логарифмическая по основанию 2; становится очевидным k=2([log2 (n-1)]-1), если nÎ[2[log2(n-1)]+1; или k=2([log2(n-1)]-1)+1= 2[log2 (n-1)]-1, если nÏ[2[log2(n-1)]+1; Так как k – максимум пересечений, то уместны неравенства: k≤2([log2 (n-1)]-1), если nÎ[2[log2(n-1)]+1; или (*) k≤2[log2 (n-1)]-1, если nÏ[2[log2(n-1)]+1; II. Найдем число дополнительных диагоналей (m), которые
Выделим в данном выпуклом n-угольнике (k+3)-угольник (k+3)-угольник отбросили существующих треугольников 1 треугольник n-угольника (всего их (n-2)),потом добавили другой ‘отбросим’ крайний треугольник и реугольник и ‘добавим’ к получившейся фигуре еще опять получили один, имеющий общую с ней сторону, (k+3)-угольник Окончательно получаем: Pkn=(n- (k+2))Аn , где (*). | |
| Просмотров: 3371 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |