| Главная » Статьи » Математика » Геометрия |
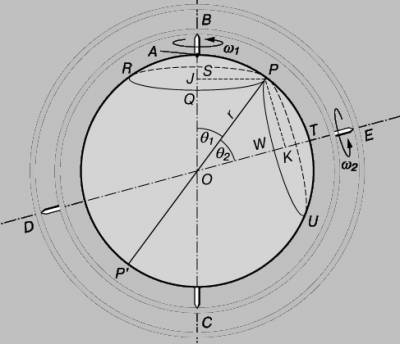 СФЕРА Sⁿ Многие величины, представляющие интерес, зависят не от одного, а от очень многих факторов, и если сама величина и каждый из определяющих его факторов могут быть охарактеризованы некоторым числом, то указанная зависимость сводится к тому, что упорядоченному набору (x1,...,xn) чисел, каждое из которых описывает состояние соответствующего фактора, становится в соответствие значение y = f(x1,...,xn) исследуемой величины, которое она приобретает при этом состоянии определяющих величину факторов. Например, площадь прямоугольника есть произведение длин его сторон; объём данного количества газа вычисляется по формуле , где R – постоянная, m – масса, T – абсолютная температура и p – давление газа. Таким образом, значение V зависит от переменной упорядоченной тройки чисел (m,T,p)или, как говорят V есть функция трёх переменных m,T,p. Мы ставим себе целью научиться исследовать функции многих переменных так же, как мы научились исследовать функции одного переменного. Как и в случае функции одного переменного, изучение функции многих числовых переменных начинается с описания их области определения. МНОЖЕСТВО Rⁿ И РАССТОЯНИЕ В НЁМ. Условимся через Rⁿ обозначать множество всех упорядоченных наборов (x1,...,xn), состоящих из n действительных чисел xiR(i =1,...,n) .XiεR Каждый такой набор будем обозначать одной буквой x = (x¹ ,...,xm) и в соответствии с удобной геометрической терминологии называть точкой множества Rⁿ. Число xi в наборе (x1 ,...,xm)называют i-й координатой точки x = (x1,...,xn). Геометрические аналогии можно продолжить и ввести на множестве Rⁿ расстояние между точками Функция определяемая формулой (1), очевидно, обладает следующими свойствами: a) b) c) d) Последнее неравенство (называемое опять-таки по геометрической аналогии неравенством треугольника) есть частный случай неравенства Минковского. Функцию, определённую на парах (x1,x2)точек некоторого множества X и обладающую свойствами a), b), c), d), называют метрикой или расстоянием в X. Множество X вместе с фиксированной в нём метрикой называют метрическим пространством. Таким образом, мы превратили Rⁿ в метрическое пространство, наделив Rⁿ метрикой, заданной соотношением (1). Из соотношения (1) следует, что при т. е. расстояние между точками Из (2), как и из (1), видно, что при n = 1 множество R1 совпадает с множеством действительных чисел, расстояние между точками которого измеряется стандартным образом посредством модуля разности чисел. ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА В RⁿОпределение 1. При δ > 0 множество
называется шаром с центром αЄ Rⁿрадиуса δ или также δ-окрестностью точки αЄ Rⁿ. Определение 2. Множество Пример 1. Rⁿ – открытое множество в Rⁿ. Пример 2. ∅ – пустое множество – вообще не содержит точек и потому может считаться удовлетворяющим определению 2, т. е. ∅ – открытое множество в Rⁿ. Пример 3. Шар B(a;r) – открытое множество в Rⁿ. Действительно, если
. Пример 4. Множество Определение 3. Множество Пример 5. Множество Сфера – множество Sⁿ точек x евклидова пространства Eⁿ¯¹, находящихся от некоторой точки x0(центр сферы) на постоянном расстоянии R(радиус сферы), т. е. . Сфера S0– пара точек, сфера S1– это окружность, сферу Sⁿ при n>2 иногда называют гиперсферой. Объём сферы Sⁿ(длина при n=1, поверхность при n=2) вычисляется по формуле , в частности,
Уравнение сферы Sⁿ в декартовых прямоугольных координатах в Eⁿ¯¹ имеет вид
(здесь xi, xi0, i=1,...,n=1, – координаты x, x0 соответственно), т. е. Сфера – (гипер)квадрика, или поверхность второго порядка специального вида. Положение какой-либо точки в пространстве относительно сферы характеризуется степенью точки. Совокупность всех сфер, относительно которых данная точка имеет одинаковую степень, составляет сеть сферы. Совокупность всех сфер, относительно которых точки некоторой прямой (радикальной оси) имеют одинаковую степень (различную для различных точек), составляет пучок сферы. НЕКОТОРЫЕ СВОЙСТВА СФЕРЫ Sⁿ.С точки зрения дифференциальной геометрии, сфера Sⁿ – риманово пространство, имеющее постоянную (гауссову при n=2 и риманову при n<2) кривизну Некоторые из таких свойств, принятые за основные, послужили отправной точкой для обобщения понятия сферы. Так, например, аффинная сфера определяется тем, что все её (аффинные) нормали пересекаются в одной точке; псевдосфера – поверхность в E3 постоянной гауссовой кривизны (но уже отрицательной); одна из интерпретаций орисферы (предельной сферы) – множество точек внутри S², определяемое уравнением также второго порядка
. На сферу Sⁿ дважды транзитивно действует ортогональная группа O (n+1) пространства Eⁿ¯¹ (2 – транзитивность означает, что для любых двух пар точек, с равными расстояниями, существует вращение – элемент O (n+1) , переводящая одну пару в другую); наконец, сфера есть однородное пространство: . С точки зрения (дифференциальной) топологии, сфера Sⁿ – замкнутое дифференцируемое многообразие, разделяющее Eⁿ¯¹ на две области и являющееся их общей границей; при этом ограниченная область, гомеоморфная Eⁿ¯¹ – это (открытый) шар, так, что сферу можно определить как его границу. Группы гомологий сферыSⁿ, n≥1:
в частности Sⁿ не стягивается в точку сама по себе, т. е. тождественное отображение Sⁿ в себя существенно. Группы гомотетий сферы Sⁿ, n≥1:
Например, И здесь понятие сфера получает обобщение. Например, дикая сфера – топологическая сфера в Eⁿ¯¹, не ограничивающая области, гомеоморфной Eⁿ¯¹; Милнора сфера (экзотическая сфера) – многообразие, гомеоморфное, но не диффеоморфное Sⁿ. Топологическое пространство, гомеоморфное сфере, называется топологической сферой. Одним из основных здесь является вопрос об условиях того, что некоторое пространство является топологической сферой. Примеры. а) Инвариантная топологическая характеристика сферы Sⁿ при n>2 не известна. О случае n=1 см. Одномерное многообразие. Для того чтобы континуум был гомеоморфен сфере S2, необходимо и достаточно, чтобы он был локально связан, содержал хотя бы одну простую замкнутую линию и чтобы всякая лежащая на нём такая линия разбивала его на две области, имеющие эту линию своей общей границей (теорема Уайлдера). б) Полное односвязное риманово пространство размерности n≥2 кривизна в) Односвязное замкнутое гладкое многообразие, (целые) гомологии которого совпадают с гомологиями Sⁿ при n n≥ 4 (при n = 3 – неизвестно). Если n=5,6, то оно также и гомеоморфно Sⁿ, при n=3.4 гипотеза остаётся, при n n≥7 диффеоморфизм не имеет места. Совершенно аналогично определяется сфера S в метрическом пространстве В нормированном пространстве E с нормой ||x||сферой называется множество
другое определение: Приложения понятия сфера чрезвычайно разнообразны. Например сферы участвуют в конструкциях новых пространств или дополнительных структур на них. Так, например, проективные пространства pⁿ можно интерпретировать как сферу Sⁿ с отождествлёнными диаметрально противоположными точками; сфера с ручками и дырами используются в теории ручек. | |
| Просмотров: 2586 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
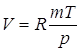
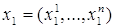 ,
, 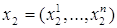 по формуле
по формуле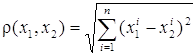 (1)
(1)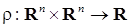 ,
,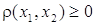 ;
;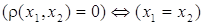 ;
;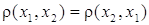 ;
;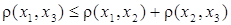 .
.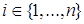
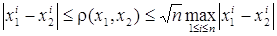 (2)
(2)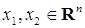 мало в том и только в том случае, когда мало отличаются соответствующие координаты этих точек.
мало в том и только в том случае, когда мало отличаются соответствующие координаты этих точек.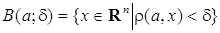
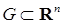 называется открытым в
называется открытым в 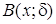 такой, что
такой, что 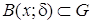 .
.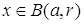 , т. е.
, т. е. 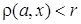 , то при
, то при 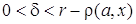 будет
будет 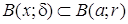 , поскольку
, поскольку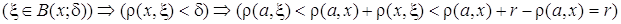
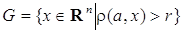 , т. е. совокупность точек, удалённых от фиксированной точки αЄ
, т. е. совокупность точек, удалённых от фиксированной точки αЄ 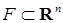 называется замкнутым в
называется замкнутым в 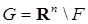 в
в 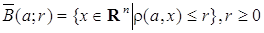 , т. е. совокупность точек, удалённых от фиксированной точки αЄ
, т. е. совокупность точек, удалённых от фиксированной точки αЄ 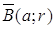 называют замкнутым шаром с центром a радиуса r.
называют замкнутым шаром с центром a радиуса r.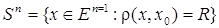
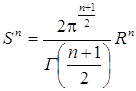
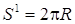
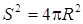
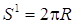 ,
, 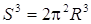 ,
, 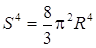 .
.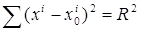
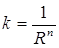 . Все геодезические линии сферы замкнуты и имеют постоянную длину 2πR – это так называемые большие окружности, т. е. пересечения с
. Все геодезические линии сферы замкнуты и имеют постоянную длину 2πR – это так называемые большие окружности, т. е. пересечения с 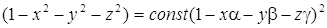
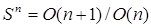
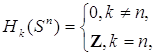
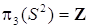 ,
, 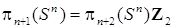 при n>2. В общем случае – для любых k и n, k>n, группы
при n>2. В общем случае – для любых k и n, k>n, группы 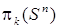 не вычислены.
не вычислены.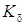 которого для всех касательных двухмерных плоскостей σδ – ограничена
которого для всех касательных двухмерных плоскостей σδ – ограничена 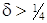 , т. е.
, т. е.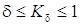 гомеоморфно
гомеоморфно 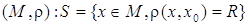 . Однако это множество, вообще говоря, может быть устроено достаточно сложно (или может быть пустым).
. Однако это множество, вообще говоря, может быть устроено достаточно сложно (или может быть пустым).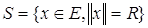 : это, по существу, произвольная, вообще говоря, бесконечномерная выпуклая (гипер)поверхность, не всегда обладающая, например, гладкостью, округлостью и т. п. полезными свойствами обычной сферы. Один из вариантов, применяющихся в топологии, – тек называемая бесконечномерная сфера – строгий индуктивный предел
: это, по существу, произвольная, вообще говоря, бесконечномерная выпуклая (гипер)поверхность, не всегда обладающая, например, гладкостью, округлостью и т. п. полезными свойствами обычной сферы. Один из вариантов, применяющихся в топологии, – тек называемая бесконечномерная сфера – строгий индуктивный предел 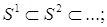
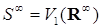 , где
, где 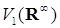 – бесконечномерное многообразие Штифеля. Для любого i оказывается, что
– бесконечномерное многообразие Штифеля. Для любого i оказывается, что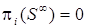 .
.