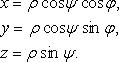| Главная » Статьи » Математика » Геометрия |
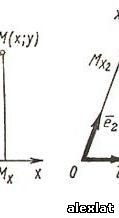
| Системы координат на плоскости Декартовы прямоугольные координаты (рис. 4.1) О - начало координат, Ох - ось абсцисс, Оy - ось ординат,
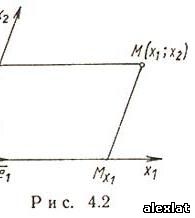
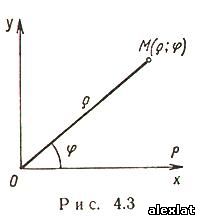
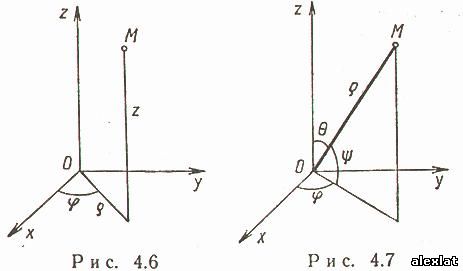
Декартовы косоугольные (афинные) координаты (рис. 4.2) О - начало координат, Ox1,Ox2 - оси координат, x1= OMx1, x2 = OMx2- координаты точки M (Mx1 - проекция точки M на ось Ox1 параллельно оси Ox2, аналогично Mx2), ē1ē2 - базисные векторы.Полярные координаты (рис. 4.3) О - полюс, Ox - полярная ось, ρ =|OM| - полярный радиус, φ - полярный угол. Главные значения ρ и φ: 0 ≤ ρ <∞ ,- π <φ ≤ π , (иногда 0 ≤ ρ <∞ ,0 ≤φ < 2π ). . Выражение декартовых прямоугольных координат через полярные χ = ρcosφ, γ = sinφ Выражение полярных координат через декартовы прямоугольные 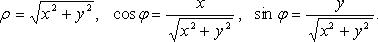
| ||
| Просмотров: 3573 | | ||
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
 - базисные векторы, x = Omx- абсцисса точки M (Mx - проекция точки M на ось Ох параллельно оси Оy),y = OMy - ордината точки M (My - проекция точки M на ось Oy параллельно оси Ox).
- базисные векторы, x = Omx- абсцисса точки M (Mx - проекция точки M на ось Ох параллельно оси Оy),y = OMy - ордината точки M (My - проекция точки M на ось Oy параллельно оси Ox).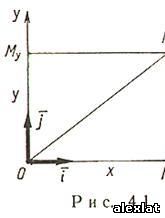
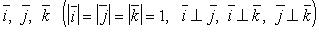 - базисные векторы. Oxy, Oxz, Oyz - координатные плоскости, χ = OMx- абсцисса точки M (Mx - проекция точки M на ось Ох параллельно плоскости Оyz), γ = OMy - ордината точки M (My - проекция точки M на ось Oy параллельно плоскости Oxz),
- базисные векторы. Oxy, Oxz, Oyz - координатные плоскости, χ = OMx- абсцисса точки M (Mx - проекция точки M на ось Ох параллельно плоскости Оyz), γ = OMy - ордината точки M (My - проекция точки M на ось Oy параллельно плоскости Oxz), 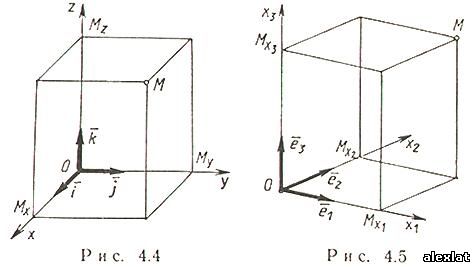
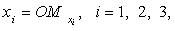 - координаты точки M
- координаты точки M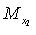
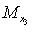
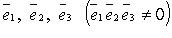
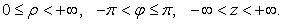
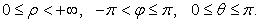
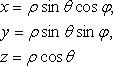 или
или