Тригонометрические функции и формулы - Геометрия - Математика - Каталог статей

Главная » Статьи » Математика » Геометрия

Тригонометрические функции и формулы

1. Число пи

Число пи — одна из главных математических постоянных. Его значение объясняется большой ролью, которую играет в науке и технике окружность и связанные с ней функции синус и косинус. Без синуса и косинуса невозможно описание волновых процессов в электронике, электротехнике, гидродинамике, механике. Например, ток и напряжение в электрической розетке описывается синусом или косинусом.

Число пи равно отношению длины окружности к удвоенному радиусу (диаметру). Оно выражается бесконечной непериодической десятичной дробью. Такие бесконечные числа называются иррациональными. Долгое время в математике существовала задача построения с помощью циркуля и линейки квадрата, площадь которого равна площади круга данного радиуса. Это так называемая задача о квадратуре круга. Она не может быть решена, т.к. отношение длины окружности к диаметру (или радиусу) не может быть выражено числом конечной длины. Число пи с точностью 17 верных знаков равно 3.14159265358979328.

2. Радиан

Радиан определяется следующим образом. Возьмем окружность произвольного радиуса, тогда угол в один радиан есть центральный угол, у которого длина дуги равна радиусу окружности. Учитывая определение числа пи, можно заключить, что углу в 360 градусов равен угол 2 * пи радиан.

3. Формула перевода радиан в градусы

Из определения числа пи, зная, что углу 2 * пи соответствует угол 360 градусов:

A_d = A_r*180/пи

Где A_d — угол в градусах, A_r — угол в радианах.

4. Формула перевода градусов в радианы

Из определения числа пи, зная, что углу 360 градусов соответствует угол 2 * пи:
A_r = A_d * пи / 180
Где Ad — угол в градусах, Ar — угол в радианах.

5.Тригонометрические функции. Прямоугольный треугольник

Рассмотрим прямоугольный треугольник, показанный на рисунке.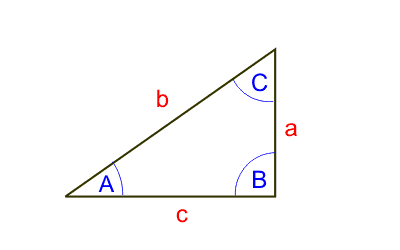

Буквами A, B, C обозначены углы, буквами a, b, c — стороны, противолежащие углам A, B, C соответственно. Угол B = 90° (прямой). Тогда тригонометрические функции определяются следующим образом:
Синус:sin(A) = a/b.
Косинус:cos(A) = c/b.
Тангенс:tg(A) = a/c.
Котангенс:ctg(A) = c/a.

6. Тригонометрические формулы для прямоугольного треугольника

a = b * sin(A)
c = b * cos(A)
a = c * tg(A)

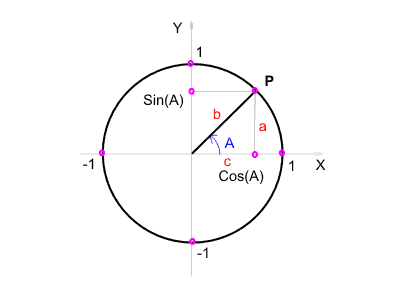
7. Тригонометрические функции. Единичная окружность.

Дадим еще одно, более общее, определение тригонометрических функций. Рассмотрим окружность единичного радиуса с центром в начале координат, показанную на рисунке.

A — угол, отсчитываемый от оси X против часовой стрелки, a, b, c — стороны прямоугольного треугольника, причем b — радиус, P — точка пересечения радиуса с окружностью с координатами (X_p, Y_p).

Синус угла A:sin(A) = a/b = a = Y_p.
Косинус угла A:cos(A) = c/b = c = X_p.
Тангенс угла A:tg(A) = a/с = Y_p/X_p.
Котангенс угла A:ctg(A) = с/a = X_p/Y_p.

При использовании тригонометрических функций принято измерять углы в радианах. Применяя определения числа пи и радиана, получим:

sin(0) = sin(пи) = 0.
sin(пи/2) = 1 .
sin(3*пи/2) = -1 .

8. Некоторые простые соотношения тригонометрических функций

tg(A) = sin (A) / cos (A).
ctg(A) = cos (A) / sin (A).
ctg(A) = 1 / tg (A)

9. Свойства тригонометрических функций

9.1. Свойства синуса

-1 ≤ sin (A) ≤ 1
Синус — нечетная функция,sin (-A) = - sin (A).
Синус — периодическая функция, период равен 2 * пи (360°).

9.2. Свойства косинуса

-1 ≤ cos(A) ≤ 1
Косинус — четная функция,cos (-A) = cos (A).
Косинус — периодическая функция, период равен 2 * пи (360°).

9.3. Свойства тангенса

Функцияtg(A)=a/с имеет разрыв для угла пи/2 (90°) и углов, отличающихся от него на ±N*пи/2 (±N*180°), т.е. когда c обращается в 0.
Тангенс — нечетная функция,tg(-A) = -tg(A).
Тангенс — периодическая функция, период равен пи (180°).

9.4. Свойства котангенса

Функция ctg(A)=c/a, имеет разрыв для угла 0° и углов, отличающихся от него на ±N*пи/2 (±N*180°), т.е. когда a обращается в 0.
Котангенс — нечетная функция,ctg (-A) = - ctg (A).
Котангенс — периодическая функция, период равен пи (180°).

10. Основные формулы треугольника

Обозначения:
A, B, C — углы треугольника, a, b, c — противолежащие стороны, R — радиус описанной окружности, r — радиус вписанной окружности, p — полупериметр, (a + b + c) / 2, S — площадь треугольника.