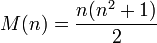Магический, или волшебный квадрат - Магический Квадрат - Математика - Каталог статей

Главная » Статьи » Математика » Магический Квадрат

Магический, или волшебный квадрат

Магический, или волшебный квадрат— это квадратная таблица n x n, заполненная n²числами, таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n².

Магические квадраты существуют для всех порядков n ≥ 1, за исключением n = 2, хотя случай n = 1 тривиален — квадрат состоит из одного числа. Минимальный нетривиальный случай показан ниже, он имеет порядок 3.

Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой , M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой

Содержание

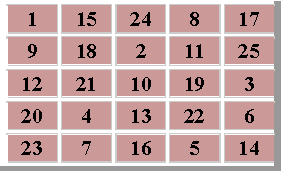
Программа для вычисления является ли массив магическим квадратом

Код программы написан на языке программирования Pascal

program magiai;

const n=3;

var a:array [1..n,1..n] of integer;

i,j,s,s1,s2:integer;

b:boolean;

{

n - размерность массива

a - массив

i,j - индексы массива

s - сумма первой строки

s1 - сумма по горизонтали

s2 - сумма по вертикали

s3 - сумма первой диагонали

s4 - сумма второй диагонали

}

begin

writeln('Программа по нахождению магической матрицы');

for i:=1 to n do {ввод массива}

for j:=1 to n do

begin

writeln('Введите [',i,',',j,'] элемент');

read(a[i,j]);

end;

s3:=0;

s4:=0;

for i:=1 to n do {вывод массива}

begin

for j:=1 to n do

begin

write(a[i,j],' ');

if i = j {подсчёт суммы первой диагонали}

then s3:=s3+a[i,j];

if i = n+1-j {подсчёт суммы второй диагонали}

then s4:=s4+a[i,j];

end;

writeln;

end;

s:= 0; {обмуление суммы}

b:= true; {начальное значения булевой переменной}

for i:=1 to n do {суммирование первой строки}

s:=s+a[1,i];

for i:=1 to n do {проход по массиву с подсчётом сумм}

begin

s1:=0;

s2:=0;

for j:=1 to n do

begin

s1:=s1+a[i,j];

s2:=s1+a[j,i];

end;

if (s<>s1) or (s<>s2) {если сумма по вертикали или по горизонтали не равны начальному значению, то выводим сообщение об этом}

then

begin

b:= false;

exit;

end;

if (s<>s3) or (s<>s4) {проверка равенства диагоналей}

then b:=false;

if b {если матрица является магической, то выводит сообщение об этом}

then writeln('Матрица является магическим квадратом');

else writeln('Матрица не является магическим квадратом');

end.

Исторически значимые магические квадраты

Квадраты с дополнительными свойствами

Дьявольский магический квадрат

Дьявольский магический квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям в обоих направлениях.

Такие квадраты называются ещё пандиагональными.

Существует 48 дьявольских магических квадратов 4×4 с точностью до поворотов и отражений. Если принять во внимание еще и их дополнительную симметрию — торические параллельные переносы, то останется только 3 существенно различных квадрата: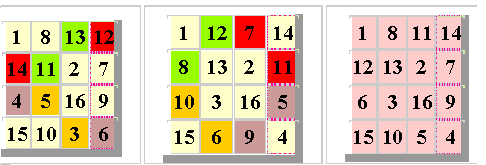

Однако было доказано, что из последнего третьего варианта простейшими перестановками чисел получаются первые два квадрата. То есть третий вариант - это базовый дьявольский квадрат, из которого различными преобразованиями можно построить все остальные.

Пандиагональные квадраты существуют для нечётного порядка n >3, для любого порядка двойной чётности n = 4k (k = 1,2,3…) и не существуют для порядка одинарной чётности n = 4k+2 (k = 1,2,3…).

Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных пандиагональных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные.

Пандиагональных квадратов пятого порядка 3600. С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.

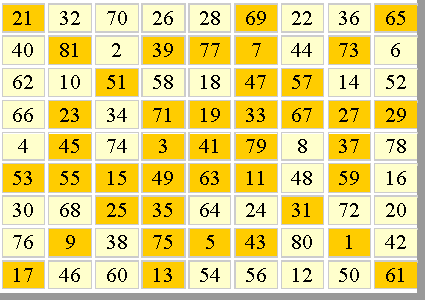
Если пандиагональный квадрат еще и ассоциативный, то он носит название идеальный

Пример идеального магического квадрата:

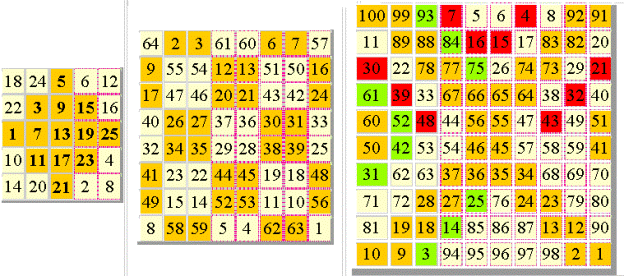
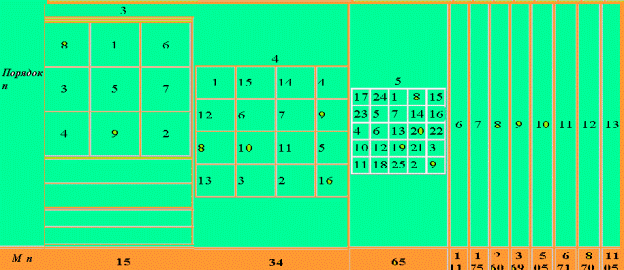
Примеры более сложных квадратов

Методически строго отработаны магические квадраты нечётного порядка и порядка двойной чётности . Формализация квадратов порядка одинарной чётности намного труднее. Сказанное иллюстрируют следующие схемы:

Cуществуют несколько десятков других методов построения магических квадратов

Шахматный подход

Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому неслучайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учётом цвета ячеек

Категория: Магический Квадрат | Добавил: alexlat (27.06.2012)

Просмотров: 5696 | Комментарии: 1 | Рейтинг: 0.0/0

Всего комментариев: 1

Порядок вывода комментариев:

Спам

г******

помогите сделать магический квадрат:
18,11,16
* * *
* 19 *

Добавлять комментарии могут только зарегистрированные пользователи.
[ Регистрация | Вход ]

Категории раздела

Пифагор Самосский [3]

Математика [45]

Алгебра Дж. Буля [1]

Алгебра [10]

Геометрия [27]

Теория вероятности [11]

Теория Графов [11]

Численные методы оптимизации [4]

Дзета-функция Римана [1]

Математическая интуиция [3]

Методы Рунге — Кутты [7]

Уравнения [17]

Векторы [5]

Математические игры [12]

Алгоритмы [3]

Нестандартный анализ [9]

Вейвлеты [3]

Анализ [8]

Графики [1]

Интегралы [3]

Задача Лагранжа [11]

Геометрия в пространстве [3]

Магический Квадрат [10]

Друзья сайта

Статистика

$AlexLat$

Программа для вычисления является ли массив магическим квадратом

Код программы написан на языке программирования Pascal

program magiai;

const n=3;

var a:array [1..n,1..n] of integer;

i,j,s,s1,s2:integer;

b:boolean;

{

n - размерность массива

a - массив

i,j - индексы массива

s - сумма первой строки

s1 - сумма по горизонтали

s2 - сумма по вертикали

s3 - сумма первой диагонали

s4 - сумма второй диагонали

}

begin

writeln('Программа по нахождению магической матрицы');

for i:=1 to n do {ввод массива}

for j:=1 to n do

begin

writeln('Введите [',i,',',j,'] элемент');

read(a[i,j]);

end;

s3:=0;

s4:=0;

for i:=1 to n do {вывод массива}

begin

for j:=1 to n do

begin

write(a[i,j],' ');

if i = j {подсчёт суммы первой диагонали}

then s3:=s3+a[i,j];

if i = n+1-j {подсчёт суммы второй диагонали}

then s4:=s4+a[i,j];

end;

writeln;

end;

s:= 0; {обмуление суммы}

b:= true; {начальное значения булевой переменной}

for i:=1 to n do {суммирование первой строки}

s:=s+a[1,i];

for i:=1 to n do {проход по массиву с подсчётом сумм}

begin

s1:=0;

s2:=0;

for j:=1 to n do

begin

s1:=s1+a[i,j];

s2:=s1+a[j,i];

end;

if (s<>s1) or (s<>s2) {если сумма по вертикали или по горизонтали не равны начальному значению, то выводим сообщение об этом}

then

begin

b:= false;

exit;

end;

end;

if (s<>s3) or (s<>s4) {проверка равенства диагоналей}

then b:=false;

if b {если матрица является магической, то выводит сообщение об этом}

then writeln('Матрица является магическим квадратом');

else writeln('Матрица не является магическим квадратом');

end.

Исторически значимые магические квадраты

Квадраты с дополнительными свойствами

Дьявольский магический квадрат

Дьявольский магический квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям в обоих направлениях.

Такие квадраты называются ещё пандиагональными.