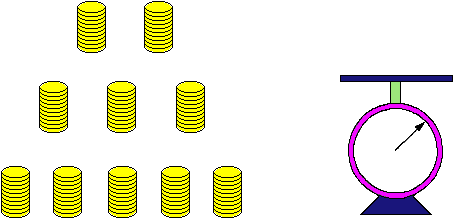 Девять задач(Nine Problems) Девять задач(Nine Problems)
1. Путешествие по замкнутому маршруту. Многим читателям, по-видимому, известна старая головоломка: «Путешественник проходит один километр на юг, поворачивает, проходит один километр на восток, еще раз поворачивает, проходит один километр на север и оказывается в том самом месте, откуда вышел. Здесь он ловким выстрелом убивает медведя. Спрашивается, какого цвета шкура убитого медведя?» Избитый ответ «белого» основан на неявном предположении, что исходной и конечной точкой замкнутого маршрута непременно должен быть Северный полюс. Не так давно было сделано открытие, что Северный полюс — отнюдь не единственная точка, удовлетворяющая всем условиям этой задачи! Можете ли вы указать еще какую-нибудь точку земного шара, из которой можно было бы пройти один километр на юг, один километр на восток, один километр на север и снова оказаться в самом начале пути?2. Покер. Двое играют в покер по следующим необычным правилам. Колоду из 52 карт они раскладывают на столе так, что могут видеть масти и значения всех карт. Первый игрок выбирает любые пять карт, второй делает то же самое, но его выбор ограничен лишь теми картами, которые остались лежать на столе. После этого первый игрок может либо оставить у себя на руках прежние пять карт, либо взять со стола новые карты (не больше пяти) и, выбрав из всех оказавшихся у него на руках карт любые пять, остальные отложить в сторону. Второй игрок вправе поступать точно таким же образом. Выигрывает тот, кто сумеет набрать пятерку карт с наибольшим числом очков. Все масти считаются одинаковыми, то есть флеши* разной масти различаются по очкам лишь в том случае, если они состоят из разных карт. Через несколько партий игроки замечают, что первый игрок всегда выигрывает, если он правильно сделает свой первый ход.Какие пять карт должен выбрать первый игрок в начале игры?
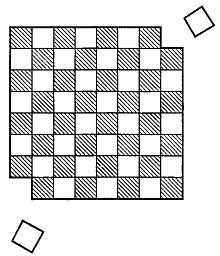
Рис. 13. Шахматная доска с выпиленными углами.3. Изуродованная шахматная доска. Для этой задачи нам потребуются шахматная доска и 32 кости домино. Размер каждой кости должен быть таким, чтобы она закрывала ровно две клетки доски, тогда 32 костями можно покрыть все 64 клетки. Предположим теперь, что две угловые клетки, расположенные на концах «белой» диагонали (рис. 13), выпилены и одной кости домино нет. Можно ли так расположить оставшиеся кости (их 31), чтобы они полностью покрыли все 62 клетки изуродованной шахматной доски? Если можно, то как? Если нельзя, то докажите, что это действительно невозможно.4. На распутье. То, о чем мы сейчас расскажем, представляет собой новый вариант давно известного типа логических головоломок. Некий логик решил провести свой отпуск в путешествии по южным морям. Однажды он оказался на острове, который, как водится в задачах этого рода, населяли племя лжецов и племя правдивых туземцев. Члены первого племени всегда лгали, члены второго — всегда говорили только правду. Путешественник дошел до места, где дорога раздваивалась, и вынужден был спросить у оказавшегося поблизости туземца, какая из двух дорог ведет в деревню. Узнать, кем был встреченный туземец — лжецом или правдивым человеком, — путешественник не мог. Все же, поразмыслив, логик задал ему одинединственный вопрос и, получив ответ, узнал, по какой дороге следует идти. Какой вопрос задал путешественник?5. Перепутанные таблички. Представьте себе, что у вас есть три коробки. В одной лежат два черных шара, во второй — два белых и в третьей — один черный шар и один белый. На коробках в соответствии с их содержимым были надписи ЧЧ, ЧБ и ББ, но кто-то их перепутал, и теперь на каждой коробке стоит надпись, не соответствующая содержимому. Чтобы узнать, какие шары лежат в каждой из трех коробок, разрешается вынимать по одному шару из коробки и, не заглядывая внутрь, возвращать его обратно. Какое минимальное число шаров нужно вынуть, чтобы с уверенностью определить содержимое всех коробок?6. В Бронкс или Бруклин? Один молодой человек живет в Манхэттене возле станции метро. У него есть две знакомые девушки. Одна из них живет в Бруклине, вторая — в Бронксе. Когда он едет к девушке из Бруклина, то садится в поезд, подходящий к платформе со стороны центра города. Когда же едет к девушке из Бронкса, то садится в поезд, идущий в центр. Поскольку обе девушки нравятся ему одинаково, он просто садится в тот поезд, который приходит первым. Таким образом, в выборе, куда ехать, он полагается на случай. Молодой человек приходит на станцию каждую субботу в разное время. И в Бруклин и в Бронкс поезда ходят с одинаковым интервалом в 10 минут. Тем не менее по каким-то непонятным причинам большую часть времени он проводит с девушкой из Бруклина; в среднем из каждых десяти поездок девять приходятся на Бруклин. Попробуйте догадаться, почему у Бруклина такой огромный перевес.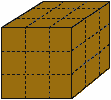
Рис. 14. Распиливание куба.7. Распиливание куба. Один плотник решил распилить кубик размером 3x3x3 см на 27 кубиков с ребром в 1 см. Это делается очень просто: надо распилить куб по шести плоскостям, не разнимая его при этом на куски (рис. 14). Можно ли уменьшить число распилов, если после каждого из них складывать отпиленные части по-новому?8. Ранний пассажир. Один человек, имеющий сезонный билет, привык каждый вечер приезжать на станцию ровно в пять часов. Его жена всегда встречает этот поезд, чтобы увезти мужа домой на машине. Однажды этот человек приехал на свою станцию в 4 ч. Стояла хорошая погода, поэтому он не стал звонить домой и пошел пешком по той дороге, по которой обычно ездила его жена. Встретив по пути жену, он сел в машину, и супруги приехали домой на 10 мин раньше обычного. Предположим, что жена всегда ездит с одной и той же скоростью, обычно выезжая из дому точно в одно и то же время, чтобы успеть к пятичасовому поезду. Можно ли определить, сколько времени муж шел пешком, пока его не подобрала машина?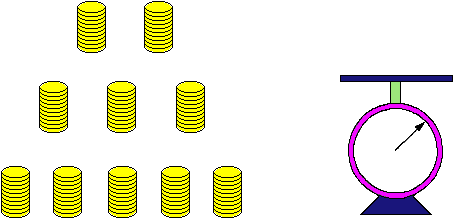
Рис. 15. Обнаружение кучки фальшивых монет.9. Фальшивые монеты. Огромный интерес вызывают задачи со взвешиванием монет или шаров. Вот одна удивительно простая задача этого типа. Имеется 10 кучек монет (рис. 15), по 10 монет в каждой. Одна из кучек целиком состоит из фальшивых монет, но какая именно — неизвестно. Известен лишь вес настоящей монеты, и, кроме того, установлено, что каждая фальшивая монета на один грамм тяжелее, чем нужно. Монеты можно взвешивать на пружинных весах. Какое минимальное число взвешиваний необходимо произвести, чтобы отыскать кучку, целиком состоящую из фальшивых монет?Ответы1. Есть ли на глобусе какая-нибудь точка, кроме Северного полюса, выйдя из которой можно пройти один километр на юг, один километр на восток и один километр на север и оказаться на прежнем месте? Конечно, есть, и не одна, а бесконечное множество та-ких точек! Можно выйти из любой точки окружности, проведенной вокруг Южного полюса на расстоянии, чуть большем километра — примерно 1,16 км (). Расстояние должно быть «чуть больше», чтобы учесть кривизну Земли. Пройдя километр на юг, а затем километр на восток, вы опишете вокруг полюса полную окружность. Пройдя еще километр на север, вы окажетесь там, откуда вышли. Следовательно, исходной точкой вашего маршрута мо-жет быть бесконечное множество точек, заполняющих окружность, центр которой совпадает с Южным полюсом, а радиус примерно равен 1,16 км. Но это еще не все. Свой путь вы можете начинать и в точках окружностей меньшего радиуса, специально подобранного так,чтобы, идя на восток, вы описывали вокруг Южного полюса два, три и т. д. оборота.2. Существует 88 наборов карт, обеспечивающих выигрыш первому игроку. Они делятся на две категории:а) четыре десятки и любая пятая карта (всего 48 наборов);б) три десятки и любая из следующих пяти пар, масть которых не совпадает с мастями выбранных десяток: туз — девятка, король — девятка, дама — девятка, валет — девятка, король — восьмерка, дама — восьмерка, дама — семерка, валет — семерка, валет — шестерка (всего 40 наборов).На вторую категорию наборов мое внимание обратили Ч. Фостер и К. Пейперс. Я никогда не встречал эти пятерки карт в опубликованных ранее решениях.3. Разместить 31 кость домино на доске, у которой вырезаны два угловых квадрата на противоположных концах диагонали, невозможно. Доказательство этого факта неожиданно просто. Две диагонально противоположные клетки должны быть одного цвета. Поэтому, если их вырезать, клеток одного цвета на доске останется на две больше, чем другого. Каждая кость домино может прикрыть два квадрата разного цвета, поскольку только такие квадраты примыкают друг к другу. После того как 30 костей закроют 60 клеток доски, свободными останутся два квадрата одинакового цвета. Они не могут находиться рядом, и поэтому их нельзя прикрыть последней костью домино.4. Потребуем, чтобы вопрос был таким, на который можно ответить только «да» или «нет». Тогда существует несколько решений, опирающихся на одну и ту же хитрость. Пусть, например, логик указал на одну из дорог и спросил туземца: «Если бы я вас спросил, ведет ли эта дорога в деревню, вы бы сказали «да»? В этом случае туземец вынужден сказать правду, даже если он лжец! Если дорога ведет в деревню, лжец должен ответить «нет», но из-за постановки вопроса он, говоря неправду, отвечает, что он бы сказал «да». Таким образом, логик может быть уверен, что дорога ведет в деревню, независимо от того, кто перед ним — лжец или правдивый человек. С другой стороны, если на самом деле дорога не ведет в деревню, лжец по тем же соображениям вынужден ответить «нет».Вот еще один подобный вопрос: «Если бы я спросил туземца из другого племени, ведет ли эта дорога в деревню, ответил бы он «да»?» Во избежание неясности из-за «вопроса о вопросе», может быть, лучше поставить вопрос несколько иначе (эту формулировку предложил У. Хэггстром): «Правда ли, что из двух утверждений: «Вы лжец» и «Эта дорога ведет в деревню» —верно одно и только одно?» Ответ «да» означает, что дорога выбрана верно, а ответ «нет» — что идти следует по другой дороге, независимо от того, лжет ли туземец или говорит правду.Д. Сиама и Дж. Маккарти обратили мое внимание на еще один забавный вариант этой задачи. «Предположим, — пишет Маккарти, — что логик в совершенстве владеет языком островитян, но не помнит, какое из двух слов («пиш» или «таш») означает «да», а какое «нет». Несмотря на свою забывчивость, он все же сможет определить, какая из двух дорог ведет в деревню. Он указывает на одну из дорог и говорит: «Если бы я спросил, ведет ли эта дорога в деревню, вы бы ответили словом «пиш»?» Если островитянин отвечает «пиш», логик может заключить, что выбранная им дорога действительно ведет в деревню, даже в том случае, если он не уверен ни в том, с кем разговаривает (с лжецом или с правдивым туземцем), ни в том, что означает слово «пиш» — «да» или «нет». Если же островитянин отвечает «таш», логик делает обратный вывод.»Г. Янцен и некоторые другие читатели сообщили мне, что если ответ туземца не обязательно должен быть «да» или «нет», то существует вопрос, с помощью которого можно найти правильный путь независимо от того, сколько дорог на перекрестке. Логик просто должен указать на все дороги, в том числе и на ту, по которой он только что шел, и спросить: «Какая из этих дорог ведет в деревню?» Правдивый туземец покажет верную дорогу, а лжец укажет на все остальные. Логик мог бы также спросить: «Какие дороги не ведут в деревню?» В этом случае лжец должен был бы показать только правильную дорогу. Надо сказать, что обе ситуации несколько ненадежны. В первом случае лжец мог бы показать только одну неправильную дорогу, а во втором он мог бы указать несколько дорог. По сути своей эти ответы были ложью, но первый был бы еще самой великой ложью, какая только возможна, а во втором содержалась бы доля правды.Вопрос о точном определении понятия «ложь» возникает даже в первых, двузначных решениях с «да» и «нет». Самое лучшее, что я могу сделать, — это привести целиком письмо, присланное в редакцию журнала Scientific American В. Кричтоном и Д. Лампиером.Как ни печально, но приходится признать, что расцвет логики приводит к упадку искусства лжи и ныне даже лжецы вынуждены все в большей и большей мере прислушиваться к доводам разума. Выражая свое сожаление, мы имеем в виду условие и решение четвертой задачи из февральского номера Scientific American. Согласившись с предложенным там решением, мы вынуждены будем сделать вывод о том, будто лжеца, строго следующего традициям своего племени, всегда можно оставить в дураках. Такая ситуация неизбежно возникает всюду, где под ложью понимают беспрекословное выполнение правил, носящих довольно произвольный, ничем не обусловленный характер.Задавая свой вопрос («Если бы я спросил, ведет ли эта дорога в деревню, ответили бы вы «да?»») и надеясь, что туземец распознает в нем как по форме, так и по содержанию составное логическое высказывание — импликацию — и сумеет разобраться в принимаемом этим высказыванием значении истинности, логик рассчитывает на известную изощренность туземца. Между тем, ничего не подозревающий туземец почти наверняка примет вопрос логика за странный способ изъяснения, связанный с изысканностью манер западных цивилизаций, и ответит на него, как на самый обычный вопрос «Эта дорога ведет в деревню?» С другой стороны, если логик с намерением подчеркнуть логический смысл вопроса пристально посмотрит на туземца, желаемая цель все оке будет достигнута, хотя туземец и заподозрит, что его каким-то образом хотят надуть. Если он по праву зовется лжецом, то в свою очередь начнет контригру и оставит логика в неведении относительно того, какая же из дорог ведет к деревне. С этой последней точки зрения предложенное решение неполно. Если же смысл термина «ложь» определить строго формально, то решение все равно нельзя считать удовлетворительным из-за его неоднозначности.Исследование однозначных решений позволяет нам лучше понять природу лжи. В логике принято называть лжецом того, кто всегда говорит нечто, противоречащее истине. Неоднозначность такого определения станет очевидной, как только мы попытаемся предсказать ответ лжеца на составное высказывание типа: «Правда ли, что если эта дорога ведет в деревню, то вы лжец?» Сможет ли туземец правильно вычислить значения истинности обоих аргументов, чтобы с их помощью определить значение истинности всей функции и в своем ответе сообщить отрицание полученного результата? Или же он займет более беспристрастную позицию и будет лгать не только другим людям, но и самому себе, подставляя при вычислении функции вместо аргументов их отрицания и сообщая отрицание вычисленного значения функции? Здесь необходимо различать просто лжеца, всегда говорящего неправду, и «честного» лжеца, постоянно изрекающего отрицание истины.Вопрос «Правда ли, что если эта дорога ведет в поселок, то вы лжец?» может считаться решением только в том случае, если лжецы, о которых говорится в условии задачи, — «честные» лжецы. Честный лжец и честный «правдивец» должны оба ответить «да», если указанная дорога не ведет в деревню, и «нет» — в противном случае. Просто лжец ответит «нет» независимо от того, куда в действительности ведет дорога. Взяв в качестве вопроса вместо импликации эквивалентность, мы получим решение, пригодное как для просто лжецов, так и для честных лжецов. Вопрос при такой замене формулируется так: «Правда ли, что эта дорога ведет в деревню тогда и только тогда, когда вы лжец?» И лжец, и правдивый туземец ответят отрицательно, если указанная дорога ведет к деревне, и утвердительно, если она не ведет к ней.Вряд ли можно надеяться, что какой-нибудь первобытный дикарь в совершенстве владеет алгеброй логики и может строго следовать правилам вычисления значений истинности булевых функций. С другой стороны, ни один хоть сколько-нибудь проницательный лжец не даст себя одурачить столь просто. Поэтому помимо двух уже названных категорий лжецов необходимо ввести в рассмотрение еще один их тип — лжеца, действующего с заранее обдуманным намерением, который всегда старается ввести того, кто с ним разговаривает, в заблуждение. Имея дело с таким противником, логик может в лучшем случае надеяться на то, что ему удастся максимально увеличить вероятность благоприятного исхода (то есть правильного выбора дороги). Ни один логический вопрос не может гарантировать успеха, ибо если лжец намеренно старается ввести своего собеседника в заблуждение, то, следуя своей тактике, он может обманывать его, нарушая при этом правила логики. В такой ситуации для логика важнее всего, чтобы избранная им тактика была психологически обоснованной. Такая линия поведения вполне допустима, поскольку, будучи примененной против «честного» лжеца и просто лжеца, она приносит еще больший эффект, чем в случае не столь легко поддающегося на удочку лжеца, намеренно вводящего собеседника в заблуждение.Учитывая все сказанное, мы предлагаем в качестве наиболее общего следующий вопрос или его моральный эквивалент: «Известно ли вам, что в этой деревне пивом угощают бесплатно?» Правдивый туземец ответит «нет» и тотчас же отправится в деревню, а логик не спеша последует за ним. Просто лжец и «честный» лжец ответят «нет» и также отправятся в деревню. Лжец, любящий вводить своих собеседников в заблуждение, будет исходить из предпосылки о том, что путешественник тоже любит морочить головы доверчивым слушателям, и изберет тактику в соответствии с этим предположением. Движимый двумя противоположными мотивами, лжец может попытаться убить двух зайцев, ответив, например, так: «Бр-р! Я терпеть не могу пива!» — и тут же побежать в деревню. Хорошего логика этим не проведешь. Достаточно предусмотрительный лжец, поразмыслив, поймет неубедительность такого ответа и, быть может, из любви к искусству решит пожертвовать своими интересами и пойдет по неправильной дороге. Лжец одержит победу по очкам, но зато логик сможет по праву отпраздновать моральную победу, ибо лжец наказан: его теперь гложет подозрение, что он упустил бесплатное пиво.5. Узнать содержимое всех коробок можно, вынув всего лишь один шар. Ключ к решению кроется в том, что все таблички на коробках не соответствуют их содержимому и вы об этом знаете. Предположим, что шар извлекается из коробки с надписью «ЧБ». Пусть вынут черный шар. Тогда вам ясно, что второй шар также черный, иначе табличка была бы правильной. Но раз вы нашли коробку с двумя черными шарами, вы сразу же можете назвать содержимое коробки с этикеткой «ББ»: в ней не могут находиться два белых шара, иначе табличка соответствовала бы содержимому коробки; в ней не могут находиться и два черных шара, поскольку вы уже нашли коробку с двумя черными шарами; таким образом, в ней должны быть один черный и один белый шар. В третьей коробке, естественно, должны быть два белых шара. Аналогичным образом задача решается и в том случае, если шар, вынутый из коробки с надписью «ЧБ», оказался не черным, а белым.6. Решение головоломки опирается на маленькую хитрость в расписании поездов. Оно составлено так, что поезд, следующий в Бронкс, всегда прибывает на минуту позже бруклинского, в то время как интервалы движения обоих поездов одинаковы — 10 минут. Отсюда ясно, что поезд в Бронкс прибудет раньше бруклинского только в том случае, если молодой человек явится на вокзал в течение этого минутного интервала. В любое же другое время (то есть в течение девятиминутного интервала) бруклинский поезд будет прибывать первым. Поскольку молодой человек приходит в совершенно произвольные моменты времени, он с вероятностью 0,9 отправляется в Бруклин.7. Разрезать куб менее чем шестью распилами нельзя. Это становится ясным, если вспомнить, что у куба шесть граней. Каждый распил означает проведение плоскости, то есть при каждом распиле появляется не более одной новой грани куба. Чтобы выпилить маленький кубик в самом центре большого куба (это единственный кубик, у которого вначале нет ни одной готовой грани), нужно провести шесть распилов. Эту задачу придумал Ф. Хоуторн.Кубы размером 2х2х2 и ЗхЗхЗ — единственные в том смысле, что, как бы вы ни складывали их части, прежде чем произвести очередной распил (разумеется, если при этом каждая часть куба где-то распиливается), все равно, пока кубы не распадутся на единичные кубики, первый придется пилить три раза, а второй — шесть.Для куба 4x4x4 понадобится провести девять распилов, если его части все время будут составлять куб. Переставляя их перед каждым распилом, можно уменьшить число последних до шести. Складывая куски куба, нужно следить за тем, чтобы каждый из них распиливался как можно ближе к середине, тогда число распилов будет минимальным. В общем случае для куба n x n x n минимальное число распилов равно 3k, где k определяется неравенством2k> n > 2k-1В общем виде эта задача была поставлена Л. Р. Фордом и Д. Р. Фулкерсоном. Однако она представляет собой лишь частный случай более общей задачи, опубликованной Л. Мозером, о минимальном числе распилов, которые необходимо произвести, чтобы разрезать прямоугольный параллелепипед размером а х b х с на единичные кубики.Ю. Дж. Патцер и Р. В. Лоуэн в своей работе «Об оптимальном способе распиливания прямоугольного параллелепипеда на единичные кубы»** пошли еще дальше. Они рассматривают n-мерные кирпичи с целыми сторонами, которые надо разделить минимальным числом плоских распилов на единичные гиперкубы. Авторы считают, что трехмерная задача «может найти применение в сыроваренной и сахарной промышленности».8. Пассажир, приехавший необычно рано, шел пешком 55 мин, прежде чем его подобрала жена. Если они приехали домой на 10 мин раньше обычного, это значит, что жена выиграла 10 мин от времени своей обычной поездки на станцию и обратно или 5 мин от времени поездки на станцию. Следовательно, она встретила мужа за пять минут до того момента (пять часов), когда обычно сажала его в машину, то есть в 4 ч 55 мин. Он вышел в четыре часа, поэтому шел 55 мин. Скорость пешехода, скорость машины и расстояние от дома до станции для решения задачи не нужны. Если вы пытались подобрать эти величины, вам, наверное, показалось, что задача чересчур сложна.
Рис. 16. График к задаче о раннем пассажире.Некоторые читатели заметили, что решение задачи намного упрощается, если нарисовать график движения (рис. 16). По горизонтальной оси отложено время, по вертикальной — расстояние. Из графика видно, что жена могла выехать из дому самое большее на 10 мин раньше, чем нужно, чтобы вовремя попасть к поезду. Нижний предел продолжительности прогулки мужа (50 мин) достигается лишь тогда, когда жена выезжает из дому ровно на десять минут раньше обычного и либо сама едет с бесконечно большой скоростью (в этом случае муж прибывает домой в тот же момент, в какой она выезжает из дому), либо муж идет с бесконечно малой скоростью (в этом случае жена встречает его у самого вокзала, откуда он вышел за 50 мин до встречи, поскольку за эти 50 мин муж так и не сдвинулся с места). «Ни одно из этих предположений, — пишет профессор Д. У. Вайзер, приславший одно из лучших решений задачи с подобным анализом, — не следует считать ошибочным: ни мастерское вождение машины женой, ни странное поведение мужа, который битый час не трогается с места, поровнявшись с пивной».9. Кучку фальшивых монет можно найти с помощью одного-единственного взвешивания. Нужно взять одну монету из первой кучки, две из второй, три — из третьей и т. д. и, наконец, все 10 монет из десятой кучки. Затем все отобранные монеты взвешиваются все вместе на пружинных весах. Лишний вес, выраженный в граммах, будет соответствовать номеру фальшивой кучки. Если, например, отобранные монеты весят на семь граммов больше, чем они должны весить, то фальшивой должна быть седьмая кучка, откуда вы взяли семь монет (каждая из которых на 1 г тяжелее настоящей). Даже при наличии одиннадцатой кучки из десяти монет этот метод все еще пригоден: отсутствие излишка в весе говорит о том, что кучка, из которой вы не взяли ни одной монеты, — фальшивая.
|