| Главная » Статьи » Математика » Математические игры |
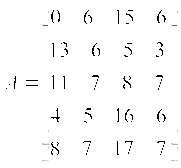
Вариант 1. 1. Для матричной игры, заданной платёжной матрицей A, найти:
РешениеМаксиминные стратегии игрока 1 определяются по формуле:
Для
строк таблицы
получаем следующие
значения : (0, 3, 7, 4, 7). Максимумов два: для 3-й строки и для 5-й. Они равны 7. Таким образом, игрок 1 имеет две максиминные стратегии: 3 и 5. Минимаксные стратегии игрока 2 ищутся по формуле:
Для
столбцов таблицы
получаем такие
значения : (13, 7, 17, 7). Игрок 2 имеет две минимаксные стратегии: 2 и 4. Седловых точек четыре: (3,2); (5,2); (3,4); (5,4). Первая цифра в скобках – номер выбранной стратегии для игрока 1, вторая – для игрока 2. Цена игры равна 7. 2. Найти решение матричной игры аналитическим методом, комбинируя его с отбрасыванием доминируемых стратегий:
Решение Доминирующей называется такая стратегия, которая во всех случаях по крайней мере не хуже, а в некоторых и лучше, чем другая. Вторая стратегия в этом случае называется доминируемой и может быть отброшена. Для игрока 1 стратегия 1 доминируется стратегией 3, а стратегия 2 доминируется стратегией 4. Таким образом, стратегии 1 и 2 могут быть отброшены, получим матрицу:
Теперь проверим стратегии игрока B. 4-й столбец доминируется 1-м, а 2-й доминируется 3-м. Отбрасываем 2-й и 4-й столбцы, получаем:
Осталась матрица 2*2. Она имеет седловую точку (2,1). Цена игры равна 4. Таким образом, из исходных стратегий наилучшей для игрока 1 будет стратегия 4 (4-я строка исходной матрицы), а для игрока 2 – стратегия 1 (1-й столбец). Значение выигрыша игрока 1 при этом будет равно 4. | |
| Просмотров: 2776 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |