| Главная » Статьи » Математика » Математические игры |
Правое или левое?
 Правое или левое? Правое или левое?(Left or Right?) Недавнее «яркое и удивительное открытие» (по выражению Роберта Оппенгеймера) существования правой и левой «ручности»* у фундаментальных частиц несет с собой много новых идей. Имеют ли все частицы во Вселенной одинаковую «ручность»? Будет ли когда-нибудь восстановлена «двуручность» природы, если обнаружатся галактики, состоящие из антивещества — вещества, сделанного из частиц, которые «ведут себя наоборот», как говорила Алиса об отражениях предметов в зеркале? Мы в нашей повседневной жизни настолько привыкли к зеркальным отражениям, что уверены, будто прекрасно их понимаем. Многих озадачит вопрос: «Почему зеркало меняет местами правое и левое, но не переворачивает верх и низ?» Вопрос еще более запутывается существованием очень простых в изготовлении зеркал, которые вовсе не переворачивают правое и левое. [История, очень похожая на историю с зеркалом, неожиданно произошла в совсем другой области — в лунной картографии. В давние времена Луну рисовали так: север помещали вверху, а юг соответственно внизу. Восточной называли левую часть карты, а западной — правую; это прямо противоположно тому, что принято называть востоком и западом на земных картах. Причина такой путаницы кроется в том, что мы смотрим на Луну, стоя спиной к Полярной звезде, отсюда естественным было назвать востоком ту часть Луны, которая обращена к востоку. У Луны восток и запад поменялись местами, как в зеркале. Позже (и сейчас) в астрономических трубах исчезли переворачивающие линзы — астрономов не беспокоило, что простым глазом мы видим одно изображение, а в трубе — перевернутое. (На астрономических снимках серп, смотрящий вправо, соответствует растущей Луне, а серп, смотрящий влево, — убывающей. Земля и Луна вращаются вокруг своих осей в одну и ту же сторону.) В атласах стали помещать Луну так, что юг оказывался наверху, а восток справа. Так что теперь на картах верх и низ поменялись местами! Дальше события развивались так. В 50-х годах астрономы забеспокоились. Им показалось, что космонавту, попавшему на Луну, будет непривычно видеть Солнце восходящим на западе и заходящим на востоке (хотя каждое такое событие происходит только раз в месяц). В 1961 году Международный астрономический союз переименовал восток Луны в запад, а запад Луны — в восток. Это все равно, что назвать правую руку при зеркальном изображении левой! На всякий случай отметим, что в соответствии с современной терминологией Море дождей находится в северо-западной части Луны (до 1951 года оно было в северо-восточной!).] И Платон в своих «Диалогах», и Лукреций в трактате «О природе вещей» описывают зеркало, сделанное из слегка изогнутого полированного металлического прямоугольника, которое изображено на рис. 87 в центре. Взглянув в это зеркало, вы увидите себя таким, каким вас видят окружающие. Машинописный текст, отраженный в таком зеркале, читается обычным образом, без всяких трудностей. 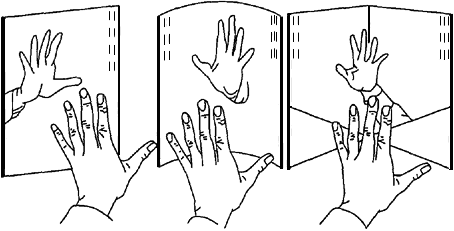 Рис. 87. Обычное зеркало и отражение в нем (слева) и два зеркала, дающие необращенные изображения (в центре и справа). Еще проще сделать зеркало, которое не меняет местами правое и левое, из двух зеркал без рамок, поставленных под прямым углом друг к другу, как показано на рис. 87. Что будет с вашим отражением, если это зеркало повернуть на 90°? Изображение перевернется вверх ногами (ранее описанное зеркало обладает этим же свойством). Симметричной называется такая структура, которая не меняется при отражении в зеркале. Она может быть наложена точка в точку на своего зеркального двойника, а асимметричная — не может. Два вида асимметричных предметов обычно различают, называя их «правыми» и «левыми». Хотя оба вида различаются между собой, вам не удастся никакими опытами обнаружить ни у одного из них такого свойства, которого не было бы у другого. Это глубоко озадачило Канта. «Что может сильнее походить на мою руку, — писал он, — чем ее отражение в зеркале? И тем не менее я не могу совместить ту руку, которую я вижу в зеркале, со своей рукой». Эта удивительная двойственность присуща структурам любого числа измерений, в том числе и того, которое больше трех. Например, отрезок прямой симметричен в одном направлении, но отрезок, составленный из длинного и короткого отрезков, асимметричен. Отражая его в зеркале, мы увидим, что длинный и короткий отрезки поменялись местами. Обращаясь к словам, как к символам, ориентированным в одном направлении, мы увидим, что в большинстве своем они симметричны, однако существуют слова-полиндромы типа «радар», «заказ», читающиеся одинаково в обоих направлениях. Существуют даже полиндромные предложения**: Draw pupil's lip upward! — Подтяни вверх губу ученика! A man, a plan, a canal — Panama! — Человек, план, канал — Панама! Egad! A base tone denotes a bad age. — Ей-богу! Низкий голос указывает на пожилой возраст. «Мадам, Адам!» — первые слова Адама (вероятно, Ева ответила на них: «Угу!»). Поэты нередко используют полиндромные звуковые эффекты. Хороший тому пример — известные лирические стихи Роберта Браунинга «Ночная встреча». Каждая строка в них написана по схеме abccba, чтобы передать в стихах шум набегающих морских волн. Мелодии также можно рассматривать как звуки, упорядоченные во времени. В пятнадцатом веке было модно сочинять полиндромные каноны***, в которых побочная тема лишь повторяла с конца к началу главную тему. Многие композиторы (в том числе Гайдн, Бах, Бетховен, Хиндемит и Шёнберг) использовали отражение мелодий для создания контрапунктных эффектов, но, как правило, перевернутые мелодии режут слух. С помощью магнитофона можно провести много забавных экспериментов по музыкальному отражению. Фортепьянная музыка, проигранная в обратном направлении, воспринимается как органная, потому что каждая нота звучит сначала чуть слышно и лишь потом достигает полного звучания. Совершенно потрясающего эффекта можно достичь, если проигрывать пленку в обратном направлении в помещении с хорошей реверберацией и записывать музыку на второй магнитофон. Тогда, перевернув вторую запись, мы услышим первоначальную мелодию, но каждому звуку будет предшествовать эхо. Музыкальное отражение можно получить и другим способом. Для этого надо повернуть пианиста на 180°, то есть так, чтобы он играл слева направо, но высокие и низкие ноты на клавиатуре поменялись бы местами. Отраженная музыка получилась бы и в том случае, если бы пианист играл как обычно, но на инструменте, отраженном в зеркале. Мелодия стала бы неузнаваемой, кроме того, возник бы неожиданный эффект замены мажорного лада минорным, и наоборот. Этот прием также использовали в канонах композиторы эпохи Возрождения и в контрапункте — композиторы, жившие позднее. Классическим примером может служить «Искусство фуги» И. С. Баха, где двенадцатая и тринадцатая фуги допускают обращение именно второго типа. Моцарт однажды написал канон, в котором побочной темой служила главная тема, читаемая с конца. Это произведение два музыканта могли бы исполнять по одним и тем же нотам, только один из них читал бы их слева направо, а другой — справа налево.  Рис. 88. Китайская монада инь — ян. Обращаясь к двумерным структурам, мы видим, что, например, христианский крест симметричен, а древний китайский религиозный символ (рис. 88) — несимметричен. Его темные и светлые участки называются инь и ян. Они символизируют все фундаментальные противоположности, в том числе правое и левое. Их комбинаторные аналоги — четные и нечетные числа. Асимметрия китайского символа делает менее удивительным тот факт, что два именно китайских физика (фамилия одного из них к тому же была Ян!) получили в 1957 году Нобелевскую премию за теоретическую работу, которая привела к открытию несохранения четности. В отличие от музыки все асимметричные рисунки и изображения можно без ущерба для эстетической ценности произведения отражать в зеркале. Рембрандт однажды сделал гравюру с зеркального отражения своего знаменитого «Снятия с креста». Высказывалось предположение, что распространенная на Западе привычка читать слева направо будет оказывать некоторое влияние на восприятие отраженного изображения. Если даже это и так, то, во всяком случае, влияние привычки читать слева направо сказывалось крайне незначительно. Большинство слов, даже набранных типографским шрифтом, несимметрично, и поэтому обычно прочесть отраженное в зеркале слово невозможно, однако не всегда. Если вы посмотрите на зеркальное отражение слов «QUALITY CHOICE», напечатанных на боковой поверхности пачки американских сигарет «Кэмел», держа пачку параллельно полу так, чтобы ее верхний конец смотрел вправо, то увидите неожиданное зрелище: слово «QUALITY» станет совершенно неудобочитаемым, а слово «CHOICE» останется без малейшего изменения****. Причина кроется в том, что написанное прописными буквами слово «CHOICE» имеет горизонтальную ось симметрии, потому его можно наложить на зеркальное отражение, перевернув вверх ногами. Другие слова, например «ТОМАТ», «НАТАША», асимметричны в горизонтальной записи, но, написанные по вертикали, приобретают ось симметрии. 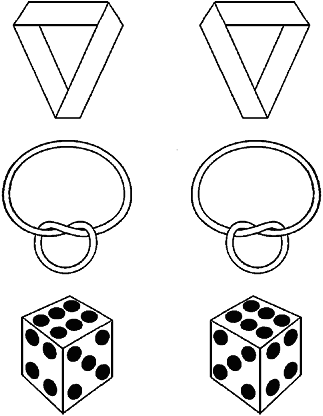 Рис. 89. Левые и правые листы Мёбиуса (вверху), узлы (в середине) и игральные кости (внизу). Рассматривая привычные трехмерные структуры, мы видим, что в них изящно сочетаются симметричные и асимметричные элементы. Большинство живых организмов с виду симметричны, исключение составляют спиральные раковины, клешни краба-скрипача, клюв у клеста и глаза плоских рыб, расположенные на одной стороне головы. Даже поведение может быть асимметричным; например, стаи летучих мышей, живущих в пещерах Карловых Вар, кружат по спирали против часовой стрелки. Предметы, сделанные руками человека, обычно выглядят симметричными, но при ближайшем рассмотрении некоторые из них все-таки оказываются несимметричными, например ножницы, лист Мёбиуса, гексафлексагоны и простые замкнутые узлы. Два узла на рис. 89 имеют одинаковую топологическую структуру, но не могут переходить друг в друга. Игральная кость также имеет две различные формы. Сумма очков на противоположных гранях должна быть равна семи, но существует два способа разметки граней; получающиеся кости являются зеркальным отражением друг друга. Скрещивая руки на груди, вы завязываете их узлом, причем это можно сделать двумя разными способами. Однако мы настолько привыкаем к одному способу, что бывает очень трудно сложить руки наоборот. Скрестите руки как обычно, возьмитесь за концы веревки и разъедините руки. Теперь узел, которым были завязаны руки, перешел на веревку. Повторите свое движение, сложив руки наоборот, — вы получите узел, являющийся зеркальным отражением первого. Существует одна интересная (и до сих пор не решенная) топологическая задача: доказать, что непрерывной деформацией замкнутой кривой зеркальные узлы нельзя перевести друг в друга. Найти доказательство этого утверждения не удалось еще никому, хотя эти два узла очень легко объединить в один симметричный (рифовый, или прямой) узел. Проделав то же с двумя узлами одной и той же «ручности», вы получите асимметричный узел. Все это далеко не тривиальные факты. Если некоторые частицы в самом деле обладают какой-то асимметрией в пространстве, то физикам придется объяснять, почему при встрече частица и античастица аннигилируют и выделяют симметричную энергию. Глядя в зеркало, Алиса размышляла над тем, можно ли пить зазеркальное молоко. Одно время считалось, что такое молоко несъедобно, потому что наш организм привык иметь дело с «левыми» молекулами и не смог бы справиться с «правыми». Сейчас ситуация значительно серьезнее. Эксперименты по сохранению четности говорят о том, что частица и античастица представляют собой две зеркальные формы одного и того же образования. Если это верно, а так считают большинство физиков, то первая же попытка Алисы попробовать зазеркальное молоко закончилась бы сильнейшим взрывом. [Скорее всего, как только Алиса приблизилась бы к антимолоку, начавшаяся аннигиляция создала бы между ними высокое давление, которое откинуло бы ее в сторону. Вспомните, как медленно горит оставленный на свободе порох.] Можно с уверенностью сказать, что физики еще долго будут обсуждать проблемы правого и левого. * * * Вопрос, заданный в начале этой главы, побудил Р. Тширги и Дж. Л. Тэйлора написать следующие письма Уважаемая редакция! В веселой и захватывающей статье Мартина Гарднера о симметрии читателю задается безнадежный вопрос: "Почему зеркало меняет местами правое и левое, но не переворачивает верх и низ?" Отвечая на него, обычно приводят подробнейшее описание хода лучей и оптических законов. Но нам кажется, что существует даже более серьезная причина, которую надо искать в области психофизиологии. Внешне люди двусторонне симметричны, однако поведение их довольно несимметрично. Умением отличать правое от левого мы, как писал в 1900 году Эрнст Мах, обязаны асимметрии наших органов чувств. Таким образом, мы представляем собой до некоторой степени асимметричный дух, вселенный во внешне симметричное тело, таков по крайней мере результат беглого исследования нашего внешнего облика. Здесь термин «симметрия» употребляется в информационном смысле и означает, что наблюдатель никаким другим способом, кроме как с помощью органов чувств, не может различить два или более объектов вокруг себя. Уточняя наблюдение, он, безусловно, может получить информацию о каких-нибудь различиях, и тогда рассматриваемая система перестанет быть симметричной. Стоя перед зеркалом, мы видим в нем внешне двусторонне симметричную структуру, и это создает у нас неправильное представление о том, что мы сами и наше отражение совершенно идентичны, а не являются энантиоморфами (существами с противоположной «ручностъю»). Поэтому мы можем мысленно повернуть в трехмерном пространстве наше отражение на 180° вокруг вертикальной оси и, совершив параллельный перенос на расстояние, равное удвоенному расстоянию до зеркала, совместить себя и отражение. При этом мы исходим из предположения, что у нашего отражения органы чувств и центральная нервная система такие оке, как у нас самих, а не как у нашего энантиоморфа. С этим и связано ошибочное утверждение, будто, когда мы поднимаем правую руку, отражение поднимает левую. Если мы теперь (что более точно) представим себе, что органы чувств внутри зеркального отражения энантиоморфны нашим, то станет ясно, что его определение правого и левого надо тоже отразить в зеркале, и поэтому, когда мы поднимаем ту руку, которая является правой для нас, отражение тоже поднимает руку, но ту, которая является правой для него. Надо снабдить зеркального двойника не нашей собственной координатной системой, а системой координат, отраженной в зеркале. Это очень легко показать. Возьмите в одну руку бумажный пакет и следующим образом переопределите координатные оси: «голова — ноги», «вперед — назад» и «рука — пакет» (вместо «левое — правое»). Встаньте теперь перед зеркалом и убедитесь в том, что, когда вы качаете головой, отражение качает головой, когда вы шевелите ногой, отражение шевелит ногой, когда вы шевелите рукой, отражение шевелит рукой, а когда вы поднимаете пакет, отражение тоже поднимает пакет. Что же случилось с перестановкой правого и левого? Асимметрия исчезла как призрак в результате простейшей процедуры: вы сделали себя внешне несимметричным относительно замены правого на левое. Теперь вам больше не удастся совместить себя и отражение поворотом на 180° вокруг вертикальной или любой другой оси. Отсюда видна энантиоморфная природа нашего отражения. Для иллюстрации того, как общепринятое соглашение о вращении предметов вокруг вертикальной оси приводит к заключению о перестановке в зеркале правого и левого не только у нас самих, но и у окружающих предметов, рассмотрим обычную карту Америки, на которой север находится вверху, а восток — справа. Чтобы увидеть зеркальное отражение этой карты, мы обычно вращаем ее по направлению к зеркалу вокруг оси север — юг. Несомненно, такая привычка появилась от того, что большая часть движений, которые мы делаем, изучая окружающие предметы, представляет собой вращение вокруг вертикальной оси. Если бы, например, карта висела на стене напротив зеркала, мы бы сначала посмотрели в карту, а потом повернулись бы вокруг вертикальной оси, чтобы увидеть отражение. В обоих случаях восток был бы у нас слева, но север оставался бы всегда наверху. Однако если для того, чтобы увидеть зеркальное отражение, мы повернем карту вокруг оси восток — запад или будем смотреть на отражение, стоя на голове, то восток у нас окажется справа, зато север переместится вниз. Таким образом, оказывается, что зеркало перевернуло верх и низ, а не правое и левое. Единственной определенной координатной системой является система, которую наблюдатель может привязать к окружающим предметам, а координатные оси при этом выбираются так, чтобы начало координат можно было поместить в любую точку пространства, доступную восприятию наблюдателя. Описывая относительное расположение частей объекта, мы обычно так располагаем координатную систему, чтобы начало координат оказалось в самом объекте. Тогда координатные оси верх — низ, сзади — спереди и правое — левое будут соответствовать осям наблюдателя. Благодаря движению объекта или самой координатной системы (то есть наблюдателя) предметы в такой системе координат вращаются и некоторые координаты объекта будут менять знак. В результате вращения предмета вокруг вертикальной оси меняются знаки его координат правое — левое и вперед — назад; вращение вокруг оси правое — левое меняет знак координат вперед — назад и верх — низ; наконец, вращение вокруг оси вперед — назад меняет знак координат верх — низ и правое — левое. Поскольку система координат связана с наблюдателем, вращение наблюдателя не влияет на знаки координат частей его тела. Таким образом, если мы смотрим на себя в зеркало, стоя на голове, мы все равно ошибочно считаем, будто зеркало меняет местами правое и левое, потому что, перевернув себя, мы одновременно перевернули и систему координат. После того как это письмо было опубликовано в Scientific American (май 1958 года), журнал получил следующее письмо от Р. С. Винера: Уважаемая редакция! Прочитав интересную заметку Тширги и Тэйлора по поводу того, почему зеркало меняет местами правое и левое и не может поменять верх и низ, я решил проверить некоторые их наблюдения. Я повесил над платяным шкафом на стену напротив зеркала карту западной части Лонг-Айленда в проливе Саунд. Стоя на голове на полу перед зеркалом, я обнаружил, что не вижу всего отражения. Пара ног — вот единственное, что мне было видно. Одну из них я узнал. Это была нога, которую я обычно называю левой, и она закрывала часть местности вокруг Бридж-порта, в то время как вторая нога находилась в окрестностях Ист-Ривер. Затем я проделал эксперимент, надев пакет на «левую» ногу. Теперь пакет болтался в районе Бридж-порта. Эксперимент показался мне не совсем завершенным, поэтому я выдвинул из комнаты шкаф, снял со стены зеркало и поставил его на пол, прислонив к стене. Я опять встал на голову перед зеркалом. Отражение двусторонне симметричного с виду существа, стоящего на голове с пакетом, надетым на ногу, так испугало меня, что я вообще прекратил эксперимент. [Удивительно, как можно запутать простой вопрос. Мы просто привыкли любой вопрос принимать серьезно, не задумываясь над тем, имеет ли смысл сама его постановка. Сказав, что зеркало меняет местами правое и левое, мы вообще не сказали ничего осмысленного. Если справа от зеркала было окно, то и я и мое отражение стоим к окну правым боком. Если под зеркалом есть пол, то и я и мое отражение стоим на полу, так что если смотреть на задачу с такой точки зрения, то никакого парадокса нет. Парадокс возникает только тогда, когда вы будете пытаться совместить себя с изображением. В обыденной жизни мы забываем о том, что сравнивать ориентацию можно, только совместив предметы в одном месте (и в одно время). Наше пространство так устроено, что мы можем переносить предметы параллельно самим себе и сравнивать их ориентацию. Именно так мы убеждаемся, что правая перчатка не совпадает с левой, а правый и левый носок не отличаются друг от друга. Сравнивать предметы на расстоянии не имеет смысла, если не проводить «в уме» операцию их совмещения. Мы привыкли еще и к тому, что в нашем пространстве тела можно поворачивать как угодно и они не будут превращаться из левого в правое или наоборот. Поэтому зеркальное изображение — новый элемент преобразования, которого нет в нашем мире. Но пусть к нам действительно пришел зеркальный человек, как бы мы его сравнили с собой? Подошли бы к нему, стали в затылок и увидели, что у него правая и левая стороны расположены наоборот. Ну а если этот зеркальный человек ходил бы еще вверх ногами? Тогда мы сказали бы, что у него переставлены верх и низ. В действительности оба утверждения тождественны, так как отличаются лишь на поворот в 180° относительно горизонтальной оси. Когда мы сравниваем себя с изображением в зеркале, то мысленно заходим за зеркало и становимся в затылок изображению. Мы уверены, что по дороге нас никто не перевернет вверх ногами. Ну а если зеркало стоит не у стены, а прикреплено к потолку или к полу, что мы видим тогда? Поменялись ли местами голова и ноги или правое и левое? Еще раз подумайте, что надо сказать относительно вашего приятеля (не его изображения, а его самого), который стал перед вами на голову: у него поменялись (по сравнению с вами) одновременно и верх и низ и правое и левое. Вы, конечно, скажете, что у него ничего не поменялось — и будете правы: вращение ничего и не меняет. Таким образом, слова «поменялись верх и низ» или «поменялись правое и левое» означают то же самое. Почему же мы этого не видим на примере с зеркалом? Просто потому, что нам легче представить себе, что мы обошли зеркало сбоку, чем перелезли через него сверху и спустились вниз головой. Если вы стоите на зеркальном полу, то вам естественней думать, что поменялись верх и низ. Чтобы совсем себя запутать, подумайте, что будет, если вы ляжете на пол ногами к висячему зеркалу. Что теперь поменялось? Таким образом, вопрос поставлен неправильно, отсюда и парадокс. Можно упростить опыт, и тогда парадокс исчезнет. Пусть на полу вертится бильярдный шар (вокруг своей вертикальной оси). Закрутим рядом другой такой же шар, но в обратную сторону (он имитирует зеркальное изображение первого). Как лучше сказать о втором шаре: что у него представлено — верх и низ или правое и левое? Ясно, что это все равно.]
| |
| Просмотров: 1436 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта