| Главная » Статьи » Математика » Математические игры |
Сэм Лойд: величайший американский головоломщик
 Сэм Лойд: величайший американский головоломщик. (Sam Loyd: America's Greatest Puzzlist) Имя Сэма Лойда вряд ли что-нибудь скажет большинству читателей этой книги, хотя в свое время он был признанным гением головоломок и пользовался широчайшей известностью. В течение полувека, вплоть до своей смерти, последовавшей в 1911 году, Лойд оставался непревзойденным мастером занимательной задачи, подлинным королем головоломок. Им опубликованы тысячи великолепных задач, в основном математического характера, многие из которых не утратили своей популярности и поныне. В действительности было два Лойда — отец и сын. После смерти Лойда-старшего сын отбросил приставку «младший» и продолжил дело отца. Сидя в своей крохотной и темной конторе в Бруклине, Лойд-младший сочинял головоломки для отделов развлечений газет и журналов, издавал книги по занимательной математике, придумывал фокусы. Но сын (Лойд-младший скончался в 1934 году) не обладал отцовской изобретательностью, и его книги мало чем отличались от других наспех составленных компиляций из работ отца. Лойд-старший родился в 1841 году в Филадельфии у «состоятельных, но честных родителей» (собственное выражение Лойда). В 1844 году его отец, агент по продаже недвижимого имущества, перевез семью в Нью-Йорк, где Сэм до 17 лет посещал общеобразовательную школу. Если бы молодой человек окончил колледж, то из него вполне мог бы выйти выдающийся математик или инженер. Но Сэм не стал поступать в колледж. Причиной тому в значительной мере явились шахматы. В течение десяти лет Лойд только и делал, что передвигал по доске шахматные фигуры. В то время шахматы были необыкновенно популярны; многие газеты вели шахматные отделы, где помещались задачи, придуманные читателями. Первая задача Лойда была опубликована одной нью-йоркской газетой, когда автору было всего 14 лет. На протяжении следующих пяти лет он настолько продуктивно сочинял шахматные головоломки, что стал весьма известен в шахматном мире. В 16 лет Лойд стал редактором отдела задач в Chess Monthly («Шахматный ежемесячник»), который тогда издавали Д. У. Фиск и молодой шахматный мастер П. Мерфи. Позже Лойд редактировал шахматные отделы в одних газетах и под различными псевдонимами регулярно посылал придуманные им задачи в другие. В 1877-1878 годах Лойд вел еженедельную шахматную страничку в приложении к журналу Scientific American. Каждая его статья начиналась с заглавной буквы, составленной из шахматных фигур задачи. Эти странички вошли в книгу Лойда «Шахматная стратегия», которую он собственноручно набрал и напечатал. Книга Лойда, содержащая 500 его избранных задач, и поныне пользуется огромным спросом*. Чаще других перепечатывалась задача Лойда, которую он придумал в 18-летнем возрасте. Эта задача может служить прекрасной иллюстрацией к умению Лойда облекать самые сложные вопросы в форму анекдота.  Рис. 40. В 1713 году шведский король Карл XII вместе со своим войском был окружен турками под Бендерами. Не обращая внимания на пули и ядра, король с одним из своих министров часто играл в шахматы. Однажды, когда у них возникла позиция, изображенная на рис. 40, Карл, игравший белыми, объявил противнику мат в три хода. В этот момент шальная пуля сбила с доски белого коня. Карл внимательно изучил новую позицию, улыбнулся и сказал, что коня ему и не нужно, поскольку и без коня он может поставить противнику мат в четыре хода. Едва он успел это сказать, как вторая пуля сбила с доски белую пешку h2. Карл невозмутимо оглядел оставшиеся на доске фигуры и объявил противнику мат в пять ходов. У этой истории есть продолжение. Через несколько лет после появления задачи Лойда один немецкий шахматист заметил, что если бы первая пуля сбила вместо коня белую ладью, то Карл все равно мог бы объявить мат в шесть ходов. Читатели, увлекающиеся шахматами, наверное, с удовольствием поразмыслят над этой замечательной «четырехсерийной» задачей.  Рис. 41. Первая головоломка, принесшая коммерческий успех, была придумана Лойдом, когда ему еще не исполнилось и двадцати лет. Она изображена на рис. 41 точно в таком виде, как ее нарисовал Лойд. Разрезав картинку вдоль пунктирных линий и переставив ее части (не сгибая их при этом), мы увидим наездников, сидящих верхом на ослах. П. Т. Барнум приобрел у Лойда право издания нескольких таких картинок и выпустил их в продажу миллионными тиражами под названием «П. Т. Барнум и его волшебные ослики». Говорят, что за несколько недель эта головоломка принесла Лойду 10000 долларов. Не утратила она своей популярности и в наши дни.
 С точки зрения математики самым интересным изобретением Лойда следует считать игру в пятнадцать. В конце сороковых годов нашего века интерес к игре в пятнадцать возобновился, коробочку с 15 квадратными шашками и сейчас еще можно встретить в магазинах игрушек. Общий вид этой головоломки показан на рис. 42. В коробочке могут свободно перемещаться 15 перенумерованных квадратных шашек. Два последних квадрата переставлены. Требуется, не вынимая из коробочки, передвинуть квадраты так, чтобы их номера расположились по порядку, а пустой квадрат оказался в правом нижнем углу. В семидесятых годах прошлого века игра в пятнадцать была в большой моде, ей посвящались даже научные статьи в математических журналах. За правильное решение головоломки Лойд назначил премию в 1000 долларов. Десятки сотен людей клялись, что они решили задачу, но ни один так и не смог вспомнить ходы, чтобы записать их и получить за это премию. Назначая премию, Лойд ничем не рисковал, ибо предложенная им задача неразрешима. Из более чем 20 миллиардов всевозможных расположений квадратов ровно половину комбинаций можно получить, передвигая квадраты из начального расположения, показанного на рис. 42. Остальные расположения квадратов, в том числе и то, которое требуется найти, если воспользоваться терминологией теории перестановок, обладают другой «четностью», а перестановки, обладающие различной четностью, не переходят друг в друга при перемещении квадратов внутри коробочки. Можно играть и по-другому: беспорядочно сложить квадратики в коробочку и, передвигая, пытаться расположить их по порядку номеров. Вероятность успеха, очевидно, равна ½. Существует простой способ, позволяющий узнать, можно ли получить данную перестановку В из любой другой перестановки А: для этого нужно лишь подсчитать число «транспозиций» (каждая транспозиция означает перестановку двух квадратов: их нужно вынуть из коробочки и поменять местами), которые необходимо совершить, чтобы превратить А в В. Если это число четно, то А и В имеют одинаковую четность и тогда, передвигая квадраты, А можно переводить в В и наоборот.
То обстоятельство, что транспозиция двух квадратиков автоматически меняет четность перестановки их номеров, положено в основу одной довольно злой задачи-шутки (разновидности игры в пятнадцать), выпущенной в продажу несколько десятков лет назад. На квадратиках, как показано на рис. 43, написаны не цифры, а буквы. На квадратах одного цвета (у нас они заштрихованы) написаны слова RATE и YOUR, на квадратах другого цвета слова MIND и PAL**. Вы показываете квадраты с получившейся на них надписью своей жертве и затем перемешиваете их как угодно. При этом вы незаметно загоняете второе R в левый верхний угол. Ваша несчастная жертва, конечно, оставит букву R в левом верхнем углу и будет пытаться расположить по порядку остальные буквы. Эта задача безнадежна, потому что, поменяв местами буквы R, вы изменили четность перестановки. В лучшем случае бедняга сможет получить "RATE YOUR MIND PAL"***. 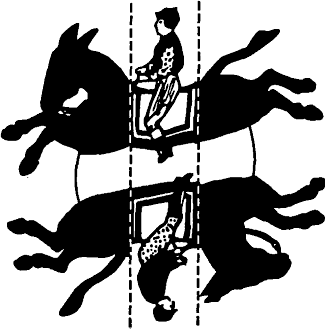 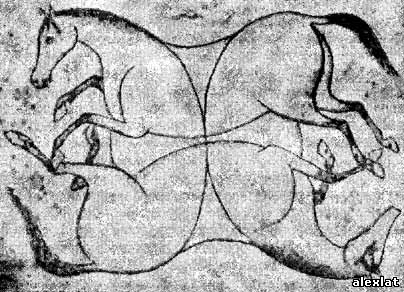 Рис. 44. Загадочная картинка Лойда «Тедди и львы». На картинке вверху — семь львов и семь охотников, на картинке внизу — восемь львов и шесть охотников. Из всех головоломок Лойда наибольшей известностью, несомненно, пользовалась его загадочная картинка «Таинственное исчезновение», запатентованная им в 1896 году. Картонный круг в центре прикрепляется к картонному квадрату. По окружности нарисованы 13 воинов, частично — на круге, частично — на квадрате. Если круг немного повернуть, части воинов соединятся уже по-другому, а один воин совсем исчезнет! Эту головоломку неоднократно публиковали, поэтому на рис. 44 показана менее популярная, но в каком-то смысле более занимательная загадочная картинка, которая называется «Тэдди и львы». В одном положении круга вы видите семь львов и семь охотников, а в другом — восемь львов и шесть охотников. Откуда берется восьмой лев? Кто из охотников исчезает и куда он девается? В 1914 году, через три года после смерти отца, Лойд-младший издал гигантскую «Энциклопедию головоломок», в которой была собрана, несомненно, самая обширная коллекция задач, когда-либо появлявшаяся в одном сборнике. Из этой сказочной, давно уже ставшей библиографической редкостью книги заимствована следующая задача. На ее примере видно, как искусно умел старый мастер переделывать любую, пусть даже самую простую задачу, для решения которой не нужно владеть ничем, кроме умения логически мыслить и обращаться с дробями, превращая ее в захватывающе увлекательную головоломку. В Сиаме очень ценятся два вида бойцовых рыб: большой белый окунь, называемый королевской рыбой, и маленький черный карп, известный под названием дьявольской рыбки. Эти виды рыб настолько враждуют между собой, что, едва завидев друг друга, бросаются в бой и бьются насмерть. Королевская рыба легко может справиться за несколько секунд с одной или двумя маленькими рыбками. Но дьявольские рыбки настолько проворны и действуют так слаженно, что втроем не уступят одной большой рыбе, однако не смогут и одолеть ее. Атакуют они так умело и изобретательно, что вчетвером приканчивают большую рыбу за какие-нибудь три минуты. Собираясь в еще большую стайку, они расправляются со своим врагом еще быстрее, причем между продолжительностью схватки и числом рыбок существует прямо пропорциональная зависимость (то есть пять рыбок расправятся с одной королевской рыбой за 2 мин 24 сек, шесть рыбок — за 2 мин ровно и т. д.). Предположим, что 4 королевские рыбы сражаются с 13 дьявольскими рыбками. Кто выиграет бой и сколько времени он продлится? Предполагается, что дьявольские рыбки действуют наиболее эффективным способом. Во избежание неоднозначности в условии сформулированной Лойдом задачи следует пояснить, что дьявольские рыбки всегда атакуют группами из трех и более рыб и, напав на королевскую рыбу, дерутся до тех пор, пока не прикончат ее. Мы не можем, например, предположить, что, пока двенадцать дьявольских рыбок осаждают четырех больших рыб, тринадцатая дьявольская рыбка носится туда и обратно, нападая на всех четырех больших рыб одновременно. Если принять предположение о том, что на большую рыбу может нападать не только целая дьявольская рыбка, но и любая ее доля, то рассуждать можно так. Если четыре дьявольские рыбки приканчивают одну королевскую рыбу за три минуты, то тринадцать дьявольских рыбок прикончат ее за 12/13 мин, а четырех королевских рыб — за 48/13 мин (то есть за 3 мин 41 7/13 сек). Но рассуждая точно таким же образом, можно показать, что двенадцать дьявольских рыбок прикончат одну королевскую рыбу за одну минуту, а четырех рыб — за четыре минуты, даже без помощи тринадцатой рыбки. Это заключение, очевидно, противоречит условию Лойда о том, что три дьявольские рыбки не могут совместными усилиями одолеть врага. * * * Профессор Артур У. Беркс сообщил мне об интересной связи, существующей между лойдовской игрой в пятнадцать и компьютером. Оба они обладают конечным числом состояний, последовательно сменяющих друг друга. Работа компьютера и решение головоломки начинаются с вполне определенного состояния. Все остальные состояния можно разделить на две группы: «допустимые», реализующиеся при указанных начальных данных, и «недопустимые», которые реализоваться не могут. Эту связь Беркс рассмотрел более подробно в свой книге****. Ответы В шахматной задаче «белые» объявляют мат в три хода, взяв пешку ладьей. Если черный слон возьмет ладью, то белые переведут своего коня на f3, тем самым вынуждая черных переставить слона. Тогда белые объявляют мат, делая ход пешкой на g4. Если бы черные взяли вместо ладьи коня, белые объявили бы шах ладьей Лh3+, черные в этом случае прикрываются слоном (Ch4), а белые, как и раньше, объявляют пешкой мат на g4. После того как пуля сбила белого коня, белые, взяв черную пешку пешкой, объявят мат в четыре хода. Если черные сделают ход слоном СеЗ, то белые ответят ладьей Лg4. Далее следует ход черного слона Cg5 и ответный ход белой ладьей Лh4+ (шах). Черный слон берет ладью, а белые объявляют мат пешкой на g4. После того как пуля сбила с доски белую пешку h2, белые объявляют мат в пять ходов, делая первый ход ладьей ЛЬ7. Если последует ход черных СеЗ, то 2. Лb1 Cg5; 3. Лh1+ Ch4; 4. Лh2!! gh; 5. g4x (мат). Если же черные делают первый ответный ход слоном Cg1, то следует: 2. Лb1 Ch2; 3. Ле1 Kph4; 4. Kpg6. На любой ход черных белые отвечают 5. Ле4х (мат). Если бы первой пулей была сбита белая ладья, а не конь, белые объявили бы мат в шесть ходов, начиная игру конем (Kf3). Тогда лучшим ходом черных был бы ход слоном Ce1, который привел бы к такому продолжению: 2. K:e1 Kph4; 3. h3 Kph5; 4. Kd3 Kph4; 5. Kf4 h5; 6. Kg6x (мат). Рис. 45. Решение головоломки с ослами и седоками. Рис. 46. Персидский рисунок XVII века, послуживший, как предполагают, источником головоломки Лойда. Наездников можно посадить на ослов (которые при этом словно по волшебству сразу поскачут галопом) таким образом, как это показано на рис. 45. На рис. 46 воспроизведен предполагаемый источник головоломки Лойда: персидский рисунок начала семнадцатого века. Что касается загадочной картинки «Тедди и львы», то бессмысленно спрашивать, который из львов исчез или который из охотников вдруг появился. Когда части смещаются, исчезают все львы и охотники, а вместо них появляются восемь новых львов, каждый на 1/8 меньше первоначального, и шесть новых охотников, каждый на 1/6 больше прежнего. Известно много решений задачи о дерущихся рыбах. Вот решение, которое дал сам Лойд. Четыре маленькие рыбки расправляются за 3 мин с одной большой рыбой, в то время как остальные дьявольские рыбки, разбившись на тройки, нападают на каждую из трех остальных больших рыб. После этого пять рыбок, объединившись, разделываются с еще одной большой рыбой за 2 мин 24 сек. Остальные маленькие рыбки в это время продолжают драться с большими. Если бы этим рыбкам (они разделились на две группы, так как дерутся с двумя королевскими рыбами) помогала еще одна дьявольская рыбка, то все три группы рыбок кончили бы бой одновременно. Поэтому сил у каждой из оставшихся в живых королевских рыб осталось ровно столько, сколько необходимо, чтобы сражаться с одной дьявольской рыбкой в течение 2 мин 24 сек. Если же на любую из королевских рыб нападает сразу не одна, а семь рыбок, то они приканчивают ее за 1/7 этого времени, то есть 20 4/7 сек. У единственной оставшейся в живых королевской рыбы сил к концу этих 20 4/7 сек хватит только на то, чтобы продержаться еще 20 4/7 сек против одной дьявольской рыбки (напомним, что на нее нападало шесть маленьких рыбок). Все же 13 дьявольских рыбок, объединив свои силы, расправляются с ней за 1/13 этого времени, то есть за 1 53/91 сек. Сложив продолжительность всех схваток — 3 мин, 2 мин 24 сек, 20 4/7 сек и 1 53/91 сек, мы найдем, что весь бой длился 5 мин 46 2/13 сек.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 1364 | | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта