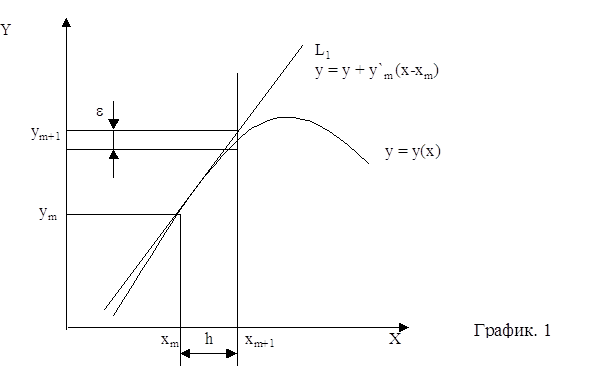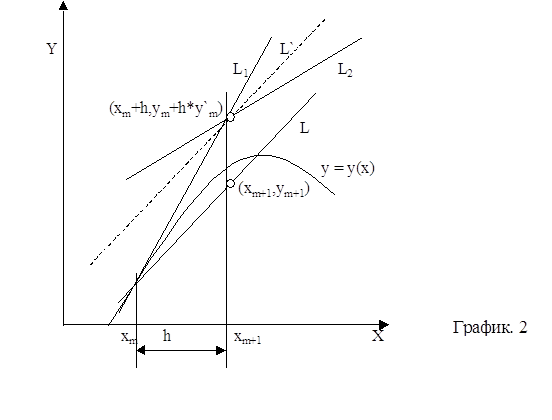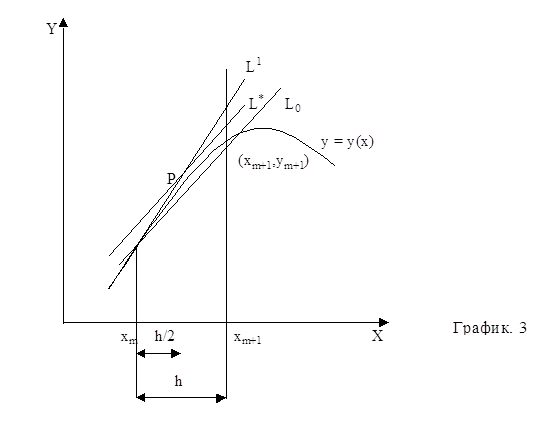| Главная » Статьи » Математика » Методы Рунге — Кутты |
| Суть метода
Разбор и рассмотрение методов, применяемых на практике для решения дифференциальных уравнений, мы начнем с их широкой категории, известной под общим названием методов Рунге-Кутта. Методы Рунге-Кутта обладают следующими свойствами: 1. Эти методы являются одноступенчатыми: чтобы найти уm+1, нужна информация о предыдущей точке xm,ym. 2. Они согласуются с рядом Тейлора вплоть до членов порядка hp, где степень р различна для различных методов и называется порядковым номером или порядком метода. 3. Они не требуют вычисления производных от f (x,y), а требуют вычисления самой функции. Рассмотрим сначала геометрическое построение и выведем некоторые формулы на основе геометрических аналогий. После этого мы подтвердим полученные результаты аналитически. Предположим, нам известна точка xm,ym на искомой кривой. Тогда мы можем провести прямую линию с тангенсом угла наклона у¢m=f(xm,ym), которая пройдет через точку xm,ym. Это построение показано на рис.1, где кривая представляет собой точное, но конечно неизвестное решение уравнения, а прямая линия L1 построена так, как это только что описано.
Тогда следующей точкой решения можно считать ту, где прямая L1 пересечет ординату, проведенную через точку x=xm+1=xm+h. Уравнение прямой L1 выглядит так: y=ym+y¢m(x-xm) так как y¢=f(xm,ym) и кроме того, xm+1=xm+h тогда уравнение примет вид ym+1=ym+h*f(xm,ym) 1.1 Ошибка при x=xm+1 показана в виде отрезка е. Очевидно, найденное таким образом приближенное значение согласуется с разложением в ряд Тейлора вплоть до членов порядка h, так что ошибка ограничения равна et=Кh2 Заметим, что хотя точка на графике 1 была показана на кривой, в действительности ym является приближенным значением и не лежит точно на кривой. Формула 1.1 описывает метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Отметим, что метод Эйлера является одним из методов Рунге-Кутта первого порядка.Рассмотрим исправленный метод Эйлера и модификационный метод Эйлера. В исправленном методе Эйлера мы находим средний тангенс угла наклона касательной для двух точек: xm,ym и xm+h,ym+hy¢m. Последняя точка есть та самая, которая в методе Эйлера обозначалась xm+1,ym+1. Геометрический процесс нахождения точки xm+1,ym+1 можно проследить по рис.2. С помощью метода Эйлера находится точка xm+h,ym+hy¢m, лежащая на прямой L1. В этой точке снова вычисляется тангенс, дает прямую L. Наконец, через точку xm,ym мы проводим прямую L, параллельную L. Точка, в которой прямая L пересечется с ординатой, восстановленной из x=xm+1=xm+h, и будет искомой точкой xm+1,ym+1. Тангенс угла наклона прямой L и прямой L равен Ф(xm,ym,h)=½[f(xm,ym)+f(xm+h,ym+y¢mh)] 1.2
где y¢m=f(xm,ym) 1.3 Уравнение линии L при этом записывается в виде y=ym+(x-xm)Ф(xm,ym,h), так что ym+1=ym+hФ(xm,ym,h). 1.4 Соотношения 1.2, 1.3, 1.4 описывают исправленный метод Эйлера.
Чтобы выяснить, насколько хорошо этот метод согласуется с разложением в ряд Тейлора, вспомним, что разложение в ряд функции f(x,y) можно записать следующим образом: f(x,y)=f(xm,ym)+(x-xm)¶f/¶x+(y-ym)¶f/¶x+¼ 1.5 где частные производные вычисляются при x=xm и y=ym. Подставляя в формулу 1.5 x=xm+h и y=ym+hy¢m и используя выражение 1.3 для y¢m, получаем f(xm+h,ym+hy¢m)=f+hfx+hffy+O(h2), где снова функция f и ее производные вычисляются в точке xm,ym. Подставляя результат в 1.2 и производя необходимые преобразования, получаем Ф(xm,ym,h)=f+h/2(fx+ffy)+O(h2). Подставим полученное выражение в 1.4 и сравним с рядом Тейлора ym+1=ym+hf+h2/2(fx+ffy)+O(h3). Как видим, исправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h2, являясь, таким образом, методом Рунге-Кутты второго порядка. Рассмотрим модификационный метод Эйлера. Рассмотрим рис.3 где первоначальное построение сделано так же, как и на рис.2. Но на этот раз мы берем точку, лежащую на пересечении этой прямой и ординатой x=x+h/2. На рисунке эта точка образована через Р, а ее ордината равна y=ym+(h/2)y¢m. Вычислим тангенс угла наклона касательной в этой точке Ф(xm,ym,h)=f+(xm+h/2,ym+h/2*y¢m), 1.6 где y¢m=f(xm,ym) 1.7 Прямая с таким наклоном, проходящая через Р, обозначена через L*. Вслед за тем, мы проводим через точку xm,ym прямую параллельную L*, и обозначаем ее через L0. Пересечение этой прямой с ординатой x=xm+h и даст искомую точку xm+1,ym+1. Уравнение прямой можно записать в виде y=ym+(x-xm)Ф(xm,ym,h), где Ф задается формулой 1.6. Поэтому ym+1=ym+hФ(xm,ym,h) 1.8 Соотношения 1.6, 1.7, 1.8 описывают так называемый модификационный метод Эйлера и является еще одним методом Рунге-Кутта второго порядка. Обобщим оба метода. Заметим, что оба метода описываются формулами вида ym+1=ym+hФ(xm,ym,h) 1.9 и в обоих случаях Ф имеет вид Ф(xm,ym,h)=a1f(xm,ym)+a2f(xm+b1h,ym+b2hy¢m), 1.10 где y¢m=f(xm,ym) 1.11 В частности, для исправленного метода Эйлера a1=a2=1/2; b1=b2=1.
В то время как для модификационного метода Эйлера a1=0, a2=1, b1=b2=1/2. Формулы 1.9, 1.10, 1.11 описывают некоторый метод типа Рунге-Кутты. Посмотрим, какого порядка метод можно рассчитывать получить в лучшем случае и каковы допустимые значения параметров a1, a2, b1 и b2 . Чтобы получить соответствие ряду Тейлора вплоть до членов степени h, в общем случае достаточно одного параметра. Чтобы получить согласование вплоть до членов степени h2, потребуется еще два параметра, так как необходимо учитывать члены h2fx и h2ffy. Так как у нас имеется всего четыре параметра, три из которых потребуются для создания согласования с рядом Тейлора вплоть до членов порядка h2, то самое лучшее, на что здесь можно рассчитывать - это метод второго порядка. В разложении f(x,y) в ряд 1.5 в окрестности точки xm,ym положим x=xm+b1h, y=ym+b2hf. Тогда f(xm+b1h,ym+b2hf)=f+b1hfx+b2hffy+O(h2), где функция и производные в правой части равенства вычислены в точке xm,ym. Тогда 1.9 можно переписать в виде ym+1=ym+h[a1f+a2f+h(a2b1fx+a2b2ffy)]+O(h3). Сравнив эту формулу с разложением в ряд Тейлора, можно переписать в виде ym+1=ym+h[a1f+a2f+h(a2b1fx+a2b2ffy)]+O(h3). Если потребовать совпадения членов hf, то a1+a2=1. Сравнивая члены, содержащие h2fx, получаем a2b1=1/2. Сравнивая члены, содержащие h2ffy, получаем a2b2=1/2. Так как мы пришли к трем уравнениям для определения четырех неизвестных, то одно из этих неизвестных можно задать произвольно, исключая, может быть, нуль, в зависимости от того, какой параметр взять в качестве произвольного. Положим, например, a2=w¹0. тогда a1=1-w, b1=b2=1/2w и соотношения 1.9, 1.10, 1.11 сведутся к ym+1=ym+h[(1-w)f(xm,ym)+wf(xm+h/2w,ym+h/2wf(xm,ym))]+O(h3) 1.12 Это наиболее общая форма записи метода Рунге-Кутта второго порядка. При w=1/2 мы получаем исправленный метод Эйлера, при w=1 получаем модификационный метод Эйлера. Для всех w, отличных от нуля, ошибка ограничения равна et=kh3 1.13 Методы Рунге-Кутта третьего и четвертого порядков можно вывести совершенно аналогично тому, как это делалось при выводе методов первого и второго порядков. Мы не будем воспроизводить выкладки, а ограничимся тем, что приведем формулы, описывающие метод четвертого порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений. Этот классический метод Рунге-Кутта описывается системой следующих пяти соотношений ym+1=ym+h/6(R1+2R2+2R3+R4) 1.14 где R1=f(xm,ym), 1.15 R2=f(xm+h/2,ym+hR1/2), 1.16 R3=f(xm+h/2,ym+hR2/2), 1.17 R4=f(xm+h/2,ym+hR3/2). 1.18 Ошибка ограничения для этого метода равна et=kh5 так что формулы 1.14-1.18 описывают метод четвертого порядка. Заметим, что при использовании этого метода функцию необходимо вычислять четыре раза. | |
| Просмотров: 2652 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |