| Главная » Статьи » Математика » Уравнения |
Формулы математической статистики
| Математическая статистика изучает общие вопросы анализа массовых
количественных данных. При этом, количественные значения рассматриваются
как случайные величины, т.е. значение величины определяется множеством
факторов случайного характера. Хорошим примером случайной величины
служат показатели финансовых рынков: цены акций на бирже, курсы валют на
рынке Forex. Обозначения:
1. Математическое ожидание (expected value) случайной величиныВ обычной жизни известно, как среднее арифметическое.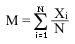 Несмотря на простоту, среднее арифметическое играет большую роль в математической статистике при анализе последовательностей случайных величин. Например, в техническом анализе рынка Форекс и других финансовых рынков большое значение имеет скользящее среднее. 3. Поле рассеяния (range - диапазон) случайной величиныR = Xmax - Xmin
4. Середина поля рассеяния (midrange)MR = Xmin + R/2 = (Xmax + Xmin)/2.
5. Дисперсия (variance) случайной величины. Одно из важнейших понятий математической статистики.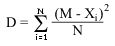
6. Cтандартное отклонение (standard deviation). Одно из важнейших понятий математической статистики.Другое название - среднеквадратичное отклонение.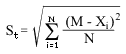
7. Оценка SДля малых N иногда используют формулу: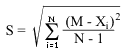
| |
| Просмотров: 4155 | Комментарии: 1 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта