В MatLab: C = E \ D;Откуда вектор минимального по норме решения равен
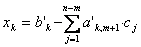 , где k = 1 m.
, где k = 1 m.
| Главная » Статьи » Математика » Уравнения |
Пусть задана система m линейных алгебраических уравнений с n неизвестными общего вида (СЛАУ) в матричной форме: A*X = B где
A – основная матрица системы (или матрица коэффициентов при неизвестных) X – вектор-столбец решений системы (вектор неизвестных) B – вектор свободных коэффициентов Решением системы такого вида называется всякий n – компонентный вектор-столбец X, обращающий матричное уравнение в тождество (равенство). Найдём решение с помощью метода последовательных исключений Жордана-Гаусса, который заключается в последовательном исключении неизвестных. Дополнительно выделим из множества решений вектор-решения минимальный по Евклидовой норме. В MatLab стандартная функция rref(A), …/matlab/toolbox/matlab/matfun/rref.m, приводит матрицу A к треугольному виду на основе классического метода исключения Гаусса с частичным выбором ведущего элемента. В данной функции реализуется следующий код: который, не меняя местами столбцы матрицы системы, приводит матрицу к диагональному виду, работая только со строками(таким образом, использование этой функции не приведетк ошибкам). % Loop over the entire matrix. % Перебор каждого элемента матрицы i = 1; j = 1; jb = []; while (i <= m) & (j <= n) % Find value and index of largest element in the remainder of column j. % Найти значение и индекс самого большого элемента в остатке от колонки j. [p,k] = max(abs(A(i:m,j))); k = k+i-1; if (p <= tol) % The column is negligible, zero it out. % Если остаток колонки незначителен, то обнуление остатка и переход на следующую иттерацию. A(i:m,j) = zeros(m-i+1,1); j = j + 1; else % Remember column index % Запоминание индекса колонки jb = [jb j]; % Swap i-th and k-th rows. % Поменияем месками i-ую и j-ую строки. A([i k],j:n) = A([k i],j:n); % Divide the pivot row by the pivot element. % Деление элементов текущей строки на текущий элемент A(i,j:n) = A(i,j:n)/A(i,j); % Subtract multiples of the pivot row from all the other rows. % Вычесть элементы текущей строки из всех других строк, начиная с j-го элемента. for k = [1:i-1 i+1:m] A(k,j:n) = A(k,j:n) - A(k,j)*A(i,j:n); end i = i + 1; j = j + 1; end end Для этого, с помощью элементарных преобразований над строками и перестановки столбцов расширенную матрицу системы A|B (матрица, образованная добавлением столбца свободных коэффициентов B к основной матрице системы A) приведём к виду:
Необходимо отметить, что коэффициенты
Тогда вектор-решения состоит из следующих компонент
Заменим
Подставляя различные числовые значения вместо Теперь из множества полученных решений необходимо выделить
минимальное по Евклидовой норме, то есть найти соответствующие значения Евклидова норма:
. Нахождение решения минимального по норме эквивалентно нахождению значений компонентов вектора-решений
Т.к. функция является положительно определенной квадратичной функцией, то частные производные по всем переменным являются линейными функциями от этих переменных::
Таким образом условием минимума функции i = 1 n-m
Построим матричную форму этой системы:
Решая эту систему получим искомое значение коэффициентов В MatLab: C = E \ D;Откуда вектор минимального по норме решения равен | |||||||||
| Просмотров: 1457 | | |||||||||
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |