| Главная » Статьи » Математика » Уравнения |
Метод неопределенных коэффициентов Если у многочлена с целыми коэффициентами рациональных корней не оказалось, можно попробовать разложить его на множители меньшей степени с целыми коэффициентами. Рассмотрим, например, уравнение . Представим левую часть в виде произведения двух квадратных трехчленов с неизвестными (неопределенными) коэффициентами: . Раскроем скобки в правой части и приведем подобные:
Теперь, приравнивая коэффициенты при одинаковых степенях x в обеих частях, получим систему уравнений
Попытка решить эту систему в
общем виде вернула бы нас назад, к решению исходного уравнения. Но целые корни,
если они существуют, нетрудно найти и подбором. Не ограничивая общности, можно
считать, что b≥q , тогда последнее уравнение
показывает, что надо рассмотреть лишь два варианта: b = 3,q =-1 ,
и b = 1q =-3.
Подставляя эти пары значений в остальные уравнения, убеждаемся, что первая из
них дает искомое разложение: Если уравнение имеет вид P(Q(x)) = 0 , где P и Q - многочлены, то замена y =Q(x) сводит его решение к решению двух уравнений меньших степеней: P(y) = 0 иQ(x) = y | |
| Просмотров: 6138 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
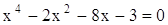
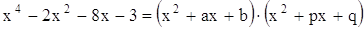
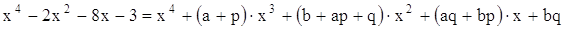
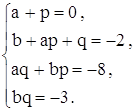
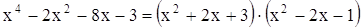 . Этот
способ решения называется методом неопределенных коэффициентов.
. Этот
способ решения называется методом неопределенных коэффициентов.