| Главная » Статьи » Математика » Уравнения |
Уравнения четвертой степени Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари. Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени x4+px³ +qx²+ix+s = 0 можно избавиться от члена px³ подстановкой x = y-p/4 . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю: . x4ax²+bx+c = 0 Идея Феррари состояла в том, чтобы представить уравнение в виде A² = B² , где левая часть – квадрат выражения A = x² + s, а правая часть – квадрат линейного уравнения B от X, коэффициенты которого зависят от S . После этого останется решить два квадратных уравнения: A= Bи A =-B и . Конечно, такое представление возможно только при специальном выборе параметра s. Удобно взять s в виде a/2+p, тогда уравнение перепишется так: . Правая часть этого уравнения – квадратный трехчлен от x. Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
b² = 2t(4t² + a² -4c) Это уравнение называется резольвентным (т.е. "разрешающим"). Относительно t оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень t0. При t = t0 правая часть уравнения (15) принимает вид , а само уравнение сводится к двум квадратным:
Их корни и дают все решения исходного уравнения. Решим для примера уравнение .x4-10x²+8x+5=0 Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде x4-10x²+8x-5 и добавим к обеим частям выражение 2sx²+s², чтобы в левой части образовался полный квадрат: .(x²+s)² = (10+2s)·x²+8x+s²-5 Теперь приравняем к нулю дискриминант правой части уравнения: 16-(10-2s)·(s²-5) =0 или, после упрощения, .s³+5s²-5s-33=0 Один из корней полученного уравнения можно угадать, перебрав делители свободного члена: s0 = -3. После подстановки этого значения получим уравнение (x²-3)² = 4x²+8x+4 = 4·(x+1)², откуда x²-3 = ±2·(x+1). Корни
образовавшихся квадратных уравнений - | |
| Просмотров: 3909 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
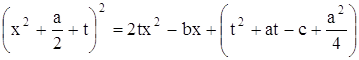 (15)
(15)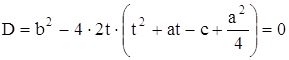 , или
, или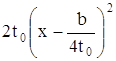
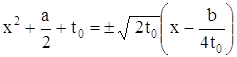 .
.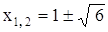 и
и 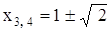 . Разумеется, в общем случае
могут получиться и комплексные корни.
. Разумеется, в общем случае
могут получиться и комплексные корни.