| Главная » Статьи » Математика » Векторы |
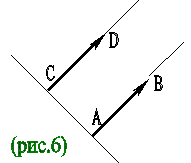
Равенство векторов. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора. Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине. И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны. Действительно, пусть векторы АВ и СD – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и СD равны, что и требовалось доказать.
| |
| Просмотров: 1200 | |
| Всего комментариев: 0 | |
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |