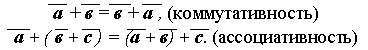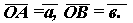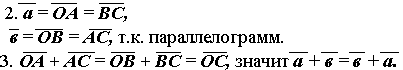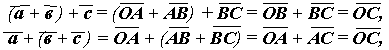Сложение векторов - Векторы - Математика - Каталог статей

Сложение векторов

Сложение векторов.

Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную "геометрическую арифметику” – арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе.

Суммой векторов а и в с координатами а₁, а₂ и в₁, в₂ называется вектор с с координатами а₁ + в₁, а₂+ в₂, т.е.

а (а₁; а₂) + в (в₁;в₂) = с (а₁ + в₁; а₂ + в₂).

Следствие: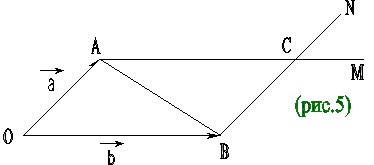

Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример.

а и в – векторы (рис.5).

Пусть

1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.

Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем: АВ + ВС =АС.

откуда и следует равенство а + ( в + с ) = (а + в) + с. Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов.

Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой "вектор”, имеющий нулевую длину и не имеющий никакого направления; этот "вектор” изображается "отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0.