| Главная » Статьи » Математика » Задача Лагранжа |
Модель II. Модель Уилсона с ограничениями на складские помещения
Модель II. Модель Уилсона с ограничениями на складские помещения Пусть торговое предприятие в течении периода времени Т должно завести и реализовать n видов товара. Соответственно обозначим: Ri - полный спрос i – го товара за время Т; C1i – стоимость хранения одной единицы i-го товара планируемом периоде времени; CSi - расходы по завозу одной партии i – го товара; Vi - объем складского помещения занимаемый одной единицей i –го товара. V - вся ёмкость складского помещения. Все эти значения считаются заранее известными. Неизвестный пока размер одной поставки i-го товара обозначим через qi, а через qio будем в дальнейшем обозначать оптимальный размер одной поставки i-го товара. 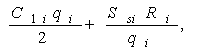 Тогда в соответствии с (2) полные издержки по завозу и хранению i-го товара будут равны: 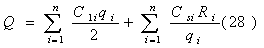 а суммарные издержки по всем видам товара принимают вид: Далее Vi * qi – объем складских помещений, которые занимают i-ый вид товара, åVi qi - объем складских помещений, занимаемых всеми видами товара и должно выполняться очевидные соотношения, 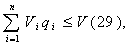 qi £ Ri, qi ³ 0 (30). Итак, приходим к следующей задаче Лагранжа: Найти минимум нелинейной функции (12) при линейных ограничениях (29) и (30). Функция Лагранжа рассматриваемой задачи (28) – (30) имеет вид: 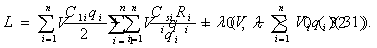 Функция Лагранжа (31) совпадает с целевой функцией (28) в случаи если в (31) 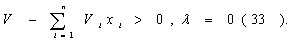 или Следуя алгоритму решения задачи Лагранжа, найдем частные производные функции (31) по всем qi и прировняем их к нулю: 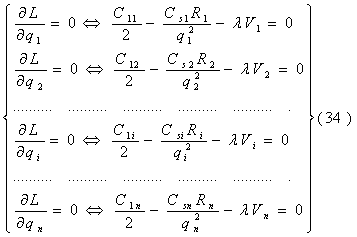 Каждое из уравнений системы (34) определяет соответствующее значение 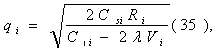 где в правой части все значения параметров известны за исключением множителя l. Для определения значения подставим выражения qi в условие (32). Получаем: 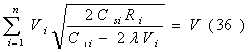  В соотношении (36) все величины, кроме l, заранее известны, т.е. оно является иррациональным уравнением с одним неизвестным. Его всегда можно разрешить относительно множителя l. Найдя значения l = l0, можно определить оптимальные величины поставок каждого из товаров по формулам: Теперь можно рассматривать конкретный пример. Пусть торговое предприятие намерено завести и реализовать товар трех видов (n = 3) объемами соответственно 24 тыс. ед, 20 тыс. ед. и 16 тыс. ед. Весь объем складских помещений составляет 18 000 куб. м. Стоимость хранения одной единицы первого вида товара 6 руб., второго – 8 руб., третьего – 10 руб. Расходы по завозу одной партии первого вида товара 1200 руб., второго – 1600 руб., третьего – 2000 руб. При этом одна единица первого вида товара занимает 3 куб. м., второго – 4 куб. м., третьего – 5 куб. м. Найти оптимальные размеры поставок каждого из видов товара. По условию имеем: R1 = 24000, R2 = 20000, R3 = 16000; C11 = 6, C12 = 8, C13 = 10; Cs1 = 1200, Cs2 = 1600, Cs3 = 2000; V1 = 3, V2 = 4, V3 = 5; V = 18000; 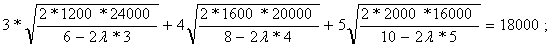 Составляем уравнение вида (36) для определения значения множителя l; 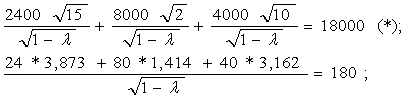 или 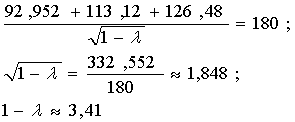 откуда lо = - 2,41. 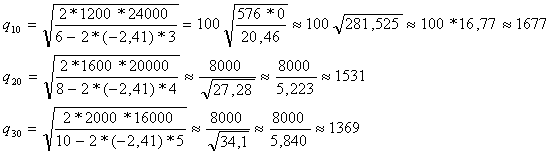 Найдем величины оптимальных поставок каждого из товаров по формулам (37): Проверим выполнимость условия (29) при найденных объемах оптимальных поставок. Должно выполняться: V1 * q1о + V2 * q2о + V3 * q3о £ V = 18000. Имеем: 3 * 1677 + 4 * 1531 + 5 * 1369 = 5031 + 6124 + 6845 = 18000. Выполнимость неравенства (29) служит подтверждением того, что объемы оптимальных поставок определены верно. Более того. Неравенство (29) в нашем примере выполнилось как равенство, что говорит о том, что при первом завозе товара все складские помещения будут заполнены максимально полно. С течением времени, при последующих завозах товара, картина будет конечно же не столь идеальной и какая та часть складских помещений будет не заполнена. Здесь можем заметить одну небольшую "уловку” в этом примере исходные данные в примере подобраны так, что иррациональное уравнение (*) вида (36) имеет во всех трех слагаемых один и тот же знаменатель, что конечно же упрощает решение уравнения. Эта "уловка” использована для облегчения рассмотрения примера, поскольку нашей главной целью в настоящий момент не является возможность разрешения иррационального уравнения. И тем не менее, возникает вопрос: а что же делать, когда при использовании этой модели на практике исходные данные будут таковы, что нашей "уловкой” воспользоваться будет невозможно. Ответ на этот вопрос достаточно прост: в современной математике разработаны десятки методов приближенных решений уравнений и потому значения множителя l можно определить из уравнения (36) приближенно с любой степенью точности. К тому же несмотря на нашу "уловку” облегчающую нахождения значения l, тем не менее мы определили его приближение. С учетом выше сказанного, можем прийти к выводу, что использованная "уловка” не сужается общностью рассмотрения модели.
| |
| Просмотров: 1296 | |
| Всего комментариев: 0 | |
Категории раздела
| Пифагор Самосский [3] |
| Математика [45] |
| Алгебра Дж. Буля [1] |
| Алгебра [10] |
| Геометрия [27] |
| Теория вероятности [11] |
| Теория Графов [11] |
| Численные методы оптимизации [4] |
| Дзета-функция Римана [1] |
| Математическая интуиция [3] |
| Методы Рунге — Кутты [7] |
| Уравнения [17] |
| Векторы [5] |
| Математические игры [12] |
| Алгоритмы [3] |
| Нестандартный анализ [9] |
| Вейвлеты [3] |
| Анализ [8] |
| Графики [1] |
| Интегралы [3] |
| Задача Лагранжа [11] |
| Геометрия в пространстве [3] |
| Магический Квадрат [10] |
Друзья сайта