Модель потребительского выбораПерейдем к рассмотрению рационального потребительского выбора в пространстве
благ с теми же отношениями предпочтения. Введем в рассмотрение функцию
полезности u(Х), согласованную с предпочтениями данного потребителя: u(Х) >
u(у) тогда и только тогда, когда Х ý У. Функцию u(Х) будем считать
непрерывно дифференцируемой.
При этих допущениях моделью потребительского оптимума служит задача Лагранжа
u(Х) ® max
при условии
å рiхi = m,
где рi - цена i - го блага, а m - денежный доход потребителя. Условия
оптимальности имеют вид 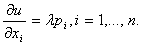 Введем для удобства обозначение
Введем для удобства обозначение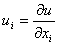 и представим условия оптимальности в форме и представим условия оптимальности в форме
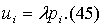 Формально эта система похожа на систему (39), описывающую оптимальность в
задаче о рационе Робинзона. Но здесь имеются и существенные отличия. Во-
первых, теперь мы отказались от предположения о суммируемости полезностей
различных благ, и ui, - не производные полезностей отдельных благ, а лишь
частные производные общей функции полезности. Во-вторых, u(Х) - это не
полезность в некоторой абсолютной количественной шкале, а лишь функция,
согласованная с предпочтениями и отражающая только порядковые отношения. Тем
не менее, перечень аналогичных свойств можно продолжить. Для любой пары благ
(i, j) в точке оптимума должны выполняться соотношения
Формально эта система похожа на систему (39), описывающую оптимальность в
задаче о рационе Робинзона. Но здесь имеются и существенные отличия. Во-
первых, теперь мы отказались от предположения о суммируемости полезностей
различных благ, и ui, - не производные полезностей отдельных благ, а лишь
частные производные общей функции полезности. Во-вторых, u(Х) - это не
полезность в некоторой абсолютной количественной шкале, а лишь функция,
согласованная с предпочтениями и отражающая только порядковые отношения. Тем
не менее, перечень аналогичных свойств можно продолжить. Для любой пары благ
(i, j) в точке оптимума должны выполняться соотношения
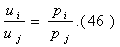 Отметим, что выражение в левой части — это норма замещения i-го блага j-м при
постоянстве объемов всех остальных благ: в пределах поверхности безразличия
должно выполняться равенство
Отметим, что выражение в левой части — это норма замещения i-го блага j-м при
постоянстве объемов всех остальных благ: в пределах поверхности безразличия
должно выполняться равенство
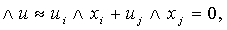 то есть
то есть
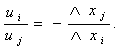 Как мы уже выяснили, значение множителя Лагранжа должно выражать предельную
полезность лимитирующего ресурса, в данном случае - денежного дохода (или,
проще, - предельную полезность денег). Но поскольку значения функции u(Х) не
являются абсолютными значениями полезности, постольку и полная полезность
денег
Как мы уже выяснили, значение множителя Лагранжа должно выражать предельную
полезность лимитирующего ресурса, в данном случае - денежного дохода (или,
проще, - предельную полезность денег). Но поскольку значения функции u(Х) не
являются абсолютными значениями полезности, постольку и полная полезность
денег
 имеет смысл лишь по отношению к выбранной шкале полезностей. То же относится
и к предельной полезности денег.
Что произойдет, если функцию полезности u(Х) заменить равносильной ей функцией u
*(Х)? Отношение предпочтения сохранится, если u*(Х) = j(u(Х)),
где j(u) - монотонно возрастающая функция. Правило дифференцирования сложной
функции позволяет утверждать, что
имеет смысл лишь по отношению к выбранной шкале полезностей. То же относится
и к предельной полезности денег.
Что произойдет, если функцию полезности u(Х) заменить равносильной ей функцией u
*(Х)? Отношение предпочтения сохранится, если u*(Х) = j(u(Х)),
где j(u) - монотонно возрастающая функция. Правило дифференцирования сложной
функции позволяет утверждать, что
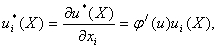 где j'(u) - значение производной dj (u)/du. Заметим, что множитель j(u)
является одним и тем же для всех благ. Поэтому условия оптимальности
ui(Х) = lpi
и
ui(Х) = l рi
определяют одно и то же положение потребительского оптимума в пространстве
благ. Различаются лишь значения множителей Лагранжа:
l = j'(u) l (47)
К этому результату можно подойти с другой стороны. Задавшись некоторым значением
m дохода, при использовании функций u(Х) и u*(Х) мы получим один и тот же
оптимальный набор благ Х0 . Общая полезность денег в одной шкале примет
значение U(m) = u(Х0), в другой
где j'(u) - значение производной dj (u)/du. Заметим, что множитель j(u)
является одним и тем же для всех благ. Поэтому условия оптимальности
ui(Х) = lpi
и
ui(Х) = l рi
определяют одно и то же положение потребительского оптимума в пространстве
благ. Различаются лишь значения множителей Лагранжа:
l = j'(u) l (47)
К этому результату можно подойти с другой стороны. Задавшись некоторым значением
m дохода, при использовании функций u(Х) и u*(Х) мы получим один и тот же
оптимальный набор благ Х0 . Общая полезность денег в одной шкале примет
значение U(m) = u(Х0), в другой 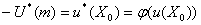 . Таким образом, при любом уровне дохода
U'(m) = j(U(m)), (48)
то есть общие полезности дохода в разных шкалах связаны между собой точно так
же, как и полезности наборов благ. А так как множитель Лагранжа в
рассматриваемой задаче - это предельная полезность денежного дохода, то,
применяя к равенству (48) правило дифференцирования сложной функции, мы снова
придем к равенству (47).
Заметим, что оптимум потребителя не всегда может быть определен в рамках
задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом
потребителя, но и условиями неотрицательности объемов благ:
. Таким образом, при любом уровне дохода
U'(m) = j(U(m)), (48)
то есть общие полезности дохода в разных шкалах связаны между собой точно так
же, как и полезности наборов благ. А так как множитель Лагранжа в
рассматриваемой задаче - это предельная полезность денежного дохода, то,
применяя к равенству (48) правило дифференцирования сложной функции, мы снова
придем к равенству (47).
Заметим, что оптимум потребителя не всегда может быть определен в рамках
задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом
потребителя, но и условиями неотрицательности объемов благ:
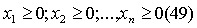 Если на бюджетной поверхности норма замещения каких-либо двух благ всюду
больше или всюду меньше отношения цен, то равенство (46) не может выполняться
ни в одной точке. Задача не имеет внутреннего решения, а имеет угловое
решение. В рамках задачи Лагранжа не могут быть описаны решения, которые
лежат на границах области, определяемой неравенствами.
Если на бюджетной поверхности норма замещения каких-либо двух благ всюду
больше или всюду меньше отношения цен, то равенство (46) не может выполняться
ни в одной точке. Задача не имеет внутреннего решения, а имеет угловое
решение. В рамках задачи Лагранжа не могут быть описаны решения, которые
лежат на границах области, определяемой неравенствами.
| 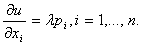 Введем для удобства обозначение
Введем для удобства обозначение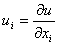 и представим условия оптимальности в форме
и представим условия оптимальности в форме
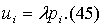 Формально эта система похожа на систему (39), описывающую оптимальность в
задаче о рационе Робинзона. Но здесь имеются и существенные отличия. Во-
первых, теперь мы отказались от предположения о суммируемости полезностей
различных благ, и ui, - не производные полезностей отдельных благ, а лишь
частные производные общей функции полезности. Во-вторых, u(Х) - это не
полезность в некоторой абсолютной количественной шкале, а лишь функция,
согласованная с предпочтениями и отражающая только порядковые отношения. Тем
не менее, перечень аналогичных свойств можно продолжить. Для любой пары благ
(i, j) в точке оптимума должны выполняться соотношения
Формально эта система похожа на систему (39), описывающую оптимальность в
задаче о рационе Робинзона. Но здесь имеются и существенные отличия. Во-
первых, теперь мы отказались от предположения о суммируемости полезностей
различных благ, и ui, - не производные полезностей отдельных благ, а лишь
частные производные общей функции полезности. Во-вторых, u(Х) - это не
полезность в некоторой абсолютной количественной шкале, а лишь функция,
согласованная с предпочтениями и отражающая только порядковые отношения. Тем
не менее, перечень аналогичных свойств можно продолжить. Для любой пары благ
(i, j) в точке оптимума должны выполняться соотношения
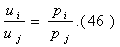 Отметим, что выражение в левой части — это норма замещения i-го блага j-м при
постоянстве объемов всех остальных благ: в пределах поверхности безразличия
должно выполняться равенство
Отметим, что выражение в левой части — это норма замещения i-го блага j-м при
постоянстве объемов всех остальных благ: в пределах поверхности безразличия
должно выполняться равенство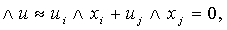 то есть
то есть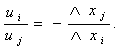 Как мы уже выяснили, значение множителя Лагранжа должно выражать предельную
полезность лимитирующего ресурса, в данном случае - денежного дохода (или,
проще, - предельную полезность денег). Но поскольку значения функции u(Х) не
являются абсолютными значениями полезности, постольку и полная полезность
денег
Как мы уже выяснили, значение множителя Лагранжа должно выражать предельную
полезность лимитирующего ресурса, в данном случае - денежного дохода (или,
проще, - предельную полезность денег). Но поскольку значения функции u(Х) не
являются абсолютными значениями полезности, постольку и полная полезность
денег
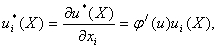 где j'(u) - значение производной dj (u)/du. Заметим, что множитель j(u)
является одним и тем же для всех благ. Поэтому условия оптимальности
ui(Х) = lpi
и
ui(Х) = l рi
определяют одно и то же положение потребительского оптимума в пространстве
благ. Различаются лишь значения множителей Лагранжа:
l = j'(u) l (47)
К этому результату можно подойти с другой стороны. Задавшись некоторым значением
m дохода, при использовании функций u(Х) и u*(Х) мы получим один и тот же
оптимальный набор благ Х0 . Общая полезность денег в одной шкале примет
значение U(m) = u(Х0), в другой
где j'(u) - значение производной dj (u)/du. Заметим, что множитель j(u)
является одним и тем же для всех благ. Поэтому условия оптимальности
ui(Х) = lpi
и
ui(Х) = l рi
определяют одно и то же положение потребительского оптимума в пространстве
благ. Различаются лишь значения множителей Лагранжа:
l = j'(u) l (47)
К этому результату можно подойти с другой стороны. Задавшись некоторым значением
m дохода, при использовании функций u(Х) и u*(Х) мы получим один и тот же
оптимальный набор благ Х0 . Общая полезность денег в одной шкале примет
значение U(m) = u(Х0), в другой 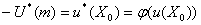 . Таким образом, при любом уровне дохода
U'(m) = j(U(m)), (48)
то есть общие полезности дохода в разных шкалах связаны между собой точно так
же, как и полезности наборов благ. А так как множитель Лагранжа в
рассматриваемой задаче - это предельная полезность денежного дохода, то,
применяя к равенству (48) правило дифференцирования сложной функции, мы снова
придем к равенству (47).
Заметим, что оптимум потребителя не всегда может быть определен в рамках
задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом
потребителя, но и условиями неотрицательности объемов благ:
. Таким образом, при любом уровне дохода
U'(m) = j(U(m)), (48)
то есть общие полезности дохода в разных шкалах связаны между собой точно так
же, как и полезности наборов благ. А так как множитель Лагранжа в
рассматриваемой задаче - это предельная полезность денежного дохода, то,
применяя к равенству (48) правило дифференцирования сложной функции, мы снова
придем к равенству (47).
Заметим, что оптимум потребителя не всегда может быть определен в рамках
задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом
потребителя, но и условиями неотрицательности объемов благ:
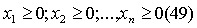 Если на бюджетной поверхности норма замещения каких-либо двух благ всюду
больше или всюду меньше отношения цен, то равенство (46) не может выполняться
ни в одной точке. Задача не имеет внутреннего решения, а имеет угловое
решение. В рамках задачи Лагранжа не могут быть описаны решения, которые
лежат на границах области, определяемой неравенствами.
Если на бюджетной поверхности норма замещения каких-либо двух благ всюду
больше или всюду меньше отношения цен, то равенство (46) не может выполняться
ни в одной точке. Задача не имеет внутреннего решения, а имеет угловое
решение. В рамках задачи Лагранжа не могут быть описаны решения, которые
лежат на границах области, определяемой неравенствами.