Смысл множителей Лагранжа
При решении задачи Лагранжа мы интересовались значениями х1,.,хn; кроме того,
нас могло интересовать экстремальное значение целевой функции f(X). Но в
процессе решения попутно было определено значение еще одной величины -
множителя Лагранжа.
Оказывается, множитель Лагранжа — весьма существенная характеристика решаемой
задачи. Чтобы смысл ее стал яснее, несколько изменим формулировку
ограничения, ничего не изменяя по существу.
Типичная экономическая ситуация характеризуется тем, что приходится искать
наиболее выгодное решение при ограниченном количестве некоторого ресурса.
Если r - заданное количество ресурса, а функция h(X) характеризует потребное
его количество для достижения точки Х, то ограничению естественно придать
форму
h(X) £ r.
По характеру задачи часто бывает ясно, что для достижения оптимума ресурс
нужно использовать полностью, так что ограничение может быть записано в виде
равенства
h(X) = r. (6)
Это условие можно представить в форме g(X) = h(Х) - r = 0. Но значительный
интерес представляет максимально достижимый уровень функции f(x) в
зависимости от имеющегося количества ресурса r. Обозначим
F(r) = max {f(X) | h(X) = r}.
В правой части - принятое обозначение условного экстремума: после
вертикальной черты выписывается условие.
Вспомним, что при обсуждении структуры лагранжиана мы интерпретировали lg(Х)
как составляющую, уравновешивающую возможный прирост максимума f(X) при
отклонении g(X) от нуля. Но отклонение g(X) от нуля есть отклонение h(Х) от
r. Если располагаемое количество ресурса получает приращение Ùr, то мы
должны ожидать приращение максимума функции f(X) на lÙr.
В действительности это соотношение носит приближенный характер. Точный
результат мы получили бы в пределе при Ùr ® 0: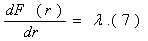 Таким образом, множитель Лагранжа характеризует скорость изменения максимума
целевой функции при изменении ограничивающей константы r в ограничении вида
(6).
В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом
была длина веревки А. Максимальная площадь оказалось равной S(A) = A2
/8. Отсюда dS(А)/dА = А/4, что в точности соответствует найденному при решении
значению l.
Таким образом, множитель Лагранжа характеризует скорость изменения максимума
целевой функции при изменении ограничивающей константы r в ограничении вида
(6).
В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом
была длина веревки А. Максимальная площадь оказалось равной S(A) = A2
/8. Отсюда dS(А)/dА = А/4, что в точности соответствует найденному при решении
значению l.
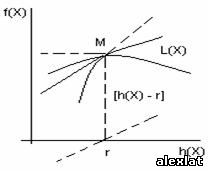 рис. 4
Приведем еще одно рассуждение. Для всевозможных точек Х найдем значения f(X)
и h(Х) и отложим эти значения в виде точек в декартовых координатах (рис. 4).
Если при каждом значении h(Х) существует максимум функции f(Х), то все точки
расположатся ниже некоторой кривой, показанной на рисунке жирной линией.
Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен
точкой М*; обозначим l наклон кривой в этой точке. Если в качестве ординаты
брать не f(X), а L(X; l) =f(X) - l [h(X) — r], то новая верхняя граница имела
бы в точке М* горизонтальную касательную. Это значит, что в исходном n-мерном
пространстве соответствующая точка М — стационарная точка функции L (X; l) с
данным значением параметра l. Таким образом, l - множитель Лагранжа.
Но жирная черная кривая — это график функции F(r), а l - его угловой
коэффициент, откуда и следует равенство (7).
рис. 4
Приведем еще одно рассуждение. Для всевозможных точек Х найдем значения f(X)
и h(Х) и отложим эти значения в виде точек в декартовых координатах (рис. 4).
Если при каждом значении h(Х) существует максимум функции f(Х), то все точки
расположатся ниже некоторой кривой, показанной на рисунке жирной линией.
Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен
точкой М*; обозначим l наклон кривой в этой точке. Если в качестве ординаты
брать не f(X), а L(X; l) =f(X) - l [h(X) — r], то новая верхняя граница имела
бы в точке М* горизонтальную касательную. Это значит, что в исходном n-мерном
пространстве соответствующая точка М — стационарная точка функции L (X; l) с
данным значением параметра l. Таким образом, l - множитель Лагранжа.
Но жирная черная кривая — это график функции F(r), а l - его угловой
коэффициент, откуда и следует равенство (7).
| 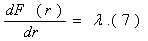 Таким образом, множитель Лагранжа характеризует скорость изменения максимума
целевой функции при изменении ограничивающей константы r в ограничении вида
(6).
В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом
была длина веревки А. Максимальная площадь оказалось равной S(A) = A2
/8. Отсюда dS(А)/dА = А/4, что в точности соответствует найденному при решении
значению l.
Таким образом, множитель Лагранжа характеризует скорость изменения максимума
целевой функции при изменении ограничивающей константы r в ограничении вида
(6).
В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом
была длина веревки А. Максимальная площадь оказалось равной S(A) = A2
/8. Отсюда dS(А)/dА = А/4, что в точности соответствует найденному при решении
значению l. рис. 4
Приведем еще одно рассуждение. Для всевозможных точек Х найдем значения f(X)
и h(Х) и отложим эти значения в виде точек в декартовых координатах (рис. 4).
Если при каждом значении h(Х) существует максимум функции f(Х), то все точки
расположатся ниже некоторой кривой, показанной на рисунке жирной линией.
Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен
точкой М*; обозначим l наклон кривой в этой точке. Если в качестве ординаты
брать не f(X), а L(X; l) =f(X) - l [h(X) — r], то новая верхняя граница имела
бы в точке М* горизонтальную касательную. Это значит, что в исходном n-мерном
пространстве соответствующая точка М — стационарная точка функции L (X; l) с
данным значением параметра l. Таким образом, l - множитель Лагранжа.
Но жирная черная кривая — это график функции F(r), а l - его угловой
коэффициент, откуда и следует равенство (7).
рис. 4
Приведем еще одно рассуждение. Для всевозможных точек Х найдем значения f(X)
и h(Х) и отложим эти значения в виде точек в декартовых координатах (рис. 4).
Если при каждом значении h(Х) существует максимум функции f(Х), то все точки
расположатся ниже некоторой кривой, показанной на рисунке жирной линией.
Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен
точкой М*; обозначим l наклон кривой в этой точке. Если в качестве ординаты
брать не f(X), а L(X; l) =f(X) - l [h(X) — r], то новая верхняя граница имела
бы в точке М* горизонтальную касательную. Это значит, что в исходном n-мерном
пространстве соответствующая точка М — стационарная точка функции L (X; l) с
данным значением параметра l. Таким образом, l - множитель Лагранжа.
Но жирная черная кривая — это график функции F(r), а l - его угловой
коэффициент, откуда и следует равенство (7).